1 1/3 In Decimal Form
monicres
Sep 18, 2025 · 6 min read
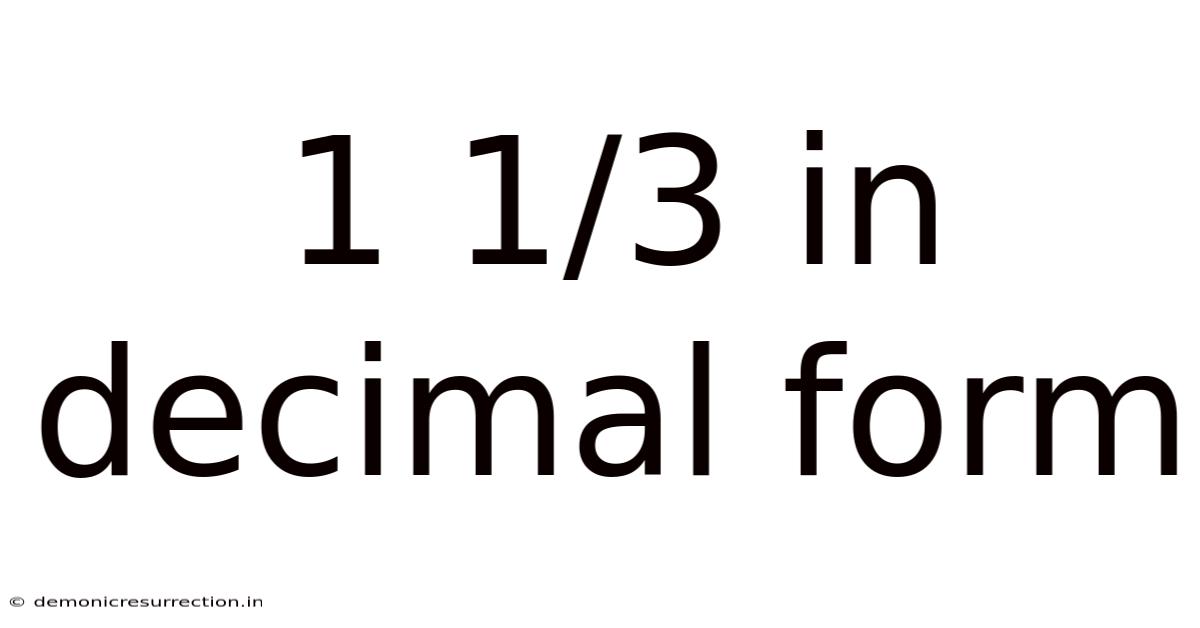
Table of Contents
Decoding 1 1/3: A Deep Dive into Decimal Conversions and Fractional Understanding
Have you ever encountered a mixed number like 1 1/3 and wondered how to express it as a decimal? This seemingly simple task unveils a fundamental concept in mathematics: converting fractions to decimals. This comprehensive guide will not only show you how to convert 1 1/3 to its decimal equivalent (and beyond!), but also delve into the underlying principles, explore practical applications, and answer frequently asked questions. Understanding this process unlocks a deeper understanding of number systems and their interconnectedness. By the end, you'll be confident in handling similar conversions and appreciate the elegance of mathematical transformations.
Understanding Fractions and Mixed Numbers
Before diving into the conversion process, let's solidify our understanding of fractions and mixed numbers. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/3, 1 is the numerator and 3 is the denominator. This means we have one part out of a total of three equal parts.
A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). 1 1/3 is a mixed number, indicating one whole unit and one-third of another unit.
Converting 1 1/3 to Decimal Form: A Step-by-Step Guide
Converting 1 1/3 to a decimal involves two primary steps:
Step 1: Convert the Mixed Number to an Improper Fraction
A mixed number is not readily convertible to a decimal. First, we need to transform it into an improper fraction, where the numerator is greater than or equal to the denominator. To do this:
- Multiply the whole number (1) by the denominator of the fraction (3): 1 * 3 = 3
- Add the result to the numerator of the fraction (1): 3 + 1 = 4
- Keep the same denominator (3).
This gives us the improper fraction 4/3.
Step 2: Divide the Numerator by the Denominator
Now that we have an improper fraction, we can perform the division to find the decimal equivalent:
4 ÷ 3 = 1.333...
The result is a repeating decimal, indicated by the ellipsis (...). The digit 3 repeats infinitely. In practice, we often round this to a certain number of decimal places depending on the required precision. For example:
- Rounded to one decimal place: 1.3
- Rounded to two decimal places: 1.33
- Rounded to three decimal places: 1.333
Therefore, 1 1/3 expressed in decimal form is approximately 1.333. The more decimal places you use, the more accurate the representation becomes, although a perfectly precise representation would require an infinite number of 3s.
Beyond 1 1/3: Mastering Decimal Conversions of Other Fractions
The method described above applies to converting any fraction or mixed number to its decimal equivalent. Let's consider a few examples:
-
2 3/4:
- Convert to an improper fraction: (2 * 4) + 3 = 11, making the improper fraction 11/4.
- Divide the numerator by the denominator: 11 ÷ 4 = 2.75. This is a terminating decimal (it ends).
-
5/8:
- This is already a proper fraction.
- Divide the numerator by the denominator: 5 ÷ 8 = 0.625. This is also a terminating decimal.
-
1/7:
- This is a proper fraction.
- Divide the numerator by the denominator: 1 ÷ 7 = 0.142857142857... This is a repeating decimal with a repeating block of six digits.
These examples highlight that decimal representations of fractions can be either terminating (ending) or repeating (continuing infinitely with a repeating pattern).
The Science Behind Decimal Conversion: Understanding Place Value
The decimal system, also known as the base-10 system, is built upon the concept of place value. Each digit in a decimal number holds a specific value based on its position relative to the decimal point. The places to the left of the decimal point represent powers of 10 (ones, tens, hundreds, and so on), while the places to the right represent negative powers of 10 (tenths, hundredths, thousandths, and so on).
When we convert a fraction to a decimal, we are essentially expressing the fractional part as a sum of these place values. For example, 0.625 can be broken down as:
- 0.6 (six-tenths)
- 0.02 (two-hundredths)
- 0.005 (five-thousandths)
This demonstrates the inherent relationship between fractions and decimals—they are simply different ways of representing the same quantity.
Real-World Applications of Decimal Conversions
The ability to convert fractions to decimals has widespread applications in various fields:
- Engineering and Construction: Precise measurements are critical, and decimal representation allows for accurate calculations and specifications.
- Finance: Dealing with monetary values frequently involves fractions (e.g., expressing interest rates or stock prices), and converting them to decimals simplifies calculations.
- Science: Scientific data often involves fractional values, and decimal representation facilitates analysis and comparisons.
- Cooking and Baking: Recipes often require fractional measurements, and converting these to decimals can aid in precise ingredient proportioning.
Frequently Asked Questions (FAQ)
Q1: How do I convert a repeating decimal back to a fraction?
A1: Converting a repeating decimal back to a fraction requires algebraic manipulation. Let's take 0.333... as an example:
- Let x = 0.333...
- Multiply both sides by 10: 10x = 3.333...
- Subtract the first equation from the second: 10x - x = 3.333... - 0.333...
- Simplify: 9x = 3
- Solve for x: x = 3/9 = 1/3
This demonstrates how a repeating decimal can be expressed as a fraction. The process varies slightly depending on the repeating pattern, but the underlying principle remains consistent.
Q2: Are there any online tools or calculators to help with decimal conversions?
A2: Yes, numerous online calculators and converters are available to assist with fraction-to-decimal conversions. These tools can be particularly helpful for complex fractions or for verifying your calculations.
Q3: What if I have a fraction with a very large denominator?
A3: Even with large denominators, the process remains the same: divide the numerator by the denominator. However, the resulting decimal might be a very long repeating or non-repeating decimal, requiring rounding for practical use.
Conclusion
Converting 1 1/3 to its decimal equivalent (approximately 1.333) is a straightforward process that underscores the fundamental relationship between fractions and decimals. By mastering this conversion, you not only gain a valuable mathematical skill but also develop a deeper appreciation for the interconnectedness of number systems. Understanding the underlying principles of place value and the techniques for handling different types of decimals empowers you to confidently tackle similar conversions in various contexts, making this a crucial skill for various academic and practical applications. Remember to practice regularly to solidify your understanding and improve your proficiency. With consistent effort, you'll become adept at navigating the world of fractions and decimals with ease and confidence.
Latest Posts
Latest Posts
-
The Hare And Tortoise Moral
Sep 18, 2025
-
The Book Thief Novel Quotes
Sep 18, 2025
-
7 Sacraments Of Catholic Church
Sep 18, 2025
-
Examples Of Arguments By Example
Sep 18, 2025
-
Orthodox Doctrine Of The Trinity
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 1/3 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.