1 X 1 0 X
monicres
Sep 19, 2025 · 7 min read
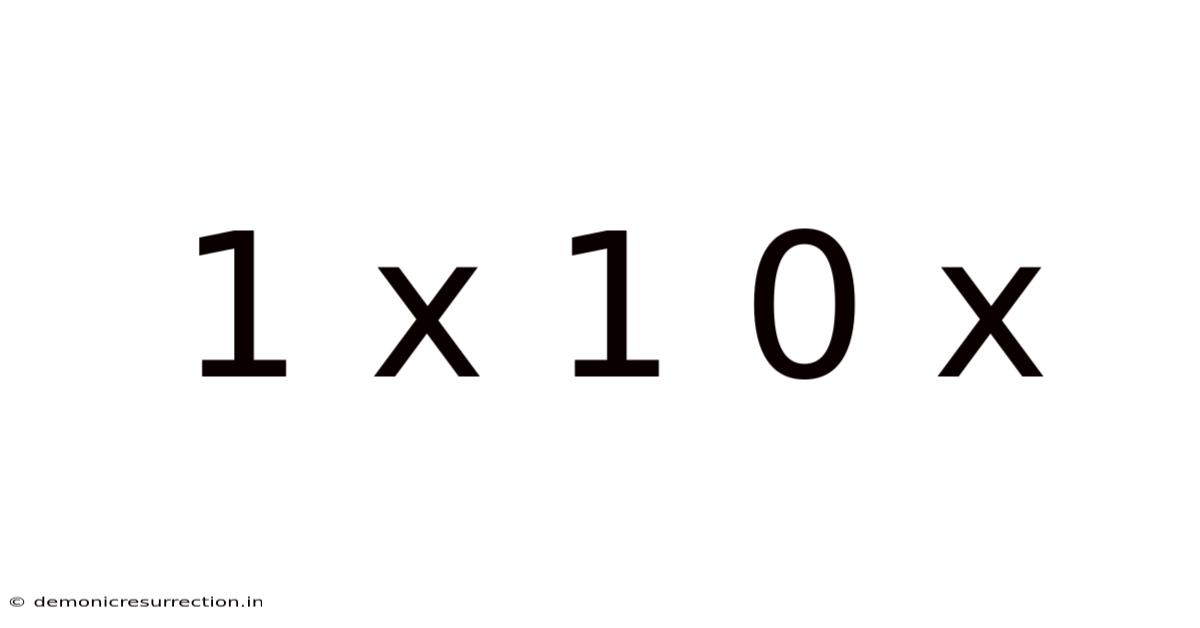
Table of Contents
Decoding 1 x 1 = 0: Exploring the World of Boolean Algebra and Logic Gates
The seemingly simple equation, 1 x 1 = 0, might initially seem paradoxical. In standard arithmetic, it's undeniably false. However, this equation finds its truth within the fascinating realm of Boolean algebra, a mathematical system crucial to the foundation of digital electronics and computer science. Understanding this equation requires delving into the principles of binary logic and the behavior of logic gates, the fundamental building blocks of all digital circuits. This article will explore the context in which 1 x 1 = 0 is valid, demystifying the concept for those unfamiliar with Boolean logic.
Introduction to Boolean Algebra
Unlike traditional arithmetic that deals with continuous values, Boolean algebra operates within a discrete system with only two possible values: 0 (representing false) and 1 (representing true). These values are not numerical quantities but rather represent logical states. The operations in Boolean algebra – primarily AND, OR, and NOT – manipulate these binary states to produce meaningful logical outcomes. This system is named after George Boole, the mathematician who formalized this system of logic in the mid-19th century. Its significance became paramount with the advent of digital computers, where every operation is fundamentally a manipulation of binary digits (bits).
Understanding the AND Operation
The AND operation, symbolized by a dot (⋅) or simply by juxtaposition (placing the variables next to each other), yields a 'true' (1) output only when both inputs are 'true' (1). Otherwise, the output is 'false' (0). Let's represent this with a truth table:
| Input A | Input B | Output (A ⋅ B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Notice that in standard arithmetic, 1 x 1 = 1. However, within the context of Boolean AND, the operation's outcome is dictated by the logical interpretation of 1 and 0.
The Role of Logic Gates
Logic gates are electronic circuits that implement Boolean operations. The AND gate, for example, physically embodies the AND operation. It has two inputs and one output, mirroring the truth table shown above. If both inputs receive a high voltage (representing 1), the output will also be high. In all other combinations of inputs, the output will be low (0).
Introducing the NOT Operation (Inversion)
The NOT operation, or inversion, is a unary operation (acting on a single input), which simply reverses the input value. If the input is 1, the output is 0, and vice versa. Its truth table is:
| Input A | Output (¬A) |
|---|---|
| 0 | 1 |
| 1 | 0 |
The NOT gate, the electronic equivalent, inverts the voltage level at its input. A high input produces a low output, and a low input results in a high output.
How 1 x 1 = 0 Becomes Possible: Introducing the XOR Gate and its applications
While the standard AND operation doesn't directly lead to 1 x 1 = 0, the exclusive OR (XOR) gate offers a pathway. XOR, denoted by ⊕, produces a 'true' (1) output only if one and only one of its inputs is true. Otherwise, the output is false (0).
| Input A | Input B | Output (A ⊕ B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Observe that in the last row of the XOR truth table, 1 ⊕ 1 = 0. This is the context where our seemingly contradictory equation finds its validity. It is not a redefinition of multiplication but rather a demonstration of a different logical operation.
The XOR gate has numerous applications in digital circuits:
- Parity Checking: XOR gates are used to detect errors in data transmission by calculating parity bits. A parity bit is an extra bit added to a data word to ensure that the total number of 1s is either even (even parity) or odd (odd parity).
- Cryptography: XOR is a fundamental operation in many encryption algorithms, as it provides a reversible way to combine data with a secret key.
- Control Circuits: XOR gates are used in various control applications, like selecting between multiple inputs or creating inverters.
- Arithmetic Logic Units (ALUs): ALUs, the brains of processors, rely heavily on logic gates including XOR gates to perform arithmetic and logical operations.
Beyond Basic Gates: Implementing More Complex Logic
The power of Boolean algebra lies in its ability to combine basic logic gates to implement complex logical functions. Through careful arrangements of AND, OR, NOT, and XOR gates, we can design circuits to accomplish any desired logical manipulation of binary data. For instance, a combination of AND and OR gates can perform a more complex operation, leading to situations where the outcome might appear unconventional from a purely arithmetic standpoint. This is because we're now operating within the rules of Boolean algebra, not standard numerical mathematics.
Implications for Computer Science and Engineering
The principles of Boolean algebra and logic gates are foundational to:
- Digital Circuit Design: Every digital circuit, from simple switches to sophisticated microprocessors, is built using logic gates. The intricate functionality of these circuits is a direct result of carefully designed arrangements of these fundamental building blocks.
- Computer Architecture: The internal workings of computers rely heavily on Boolean logic. CPU operations, data storage, and memory management all operate based on these principles.
- Programming Languages: Programming languages often incorporate Boolean operators (AND, OR, NOT) to control program flow and evaluate logical conditions.
- Database Systems: Boolean logic is fundamental in designing efficient database queries, allowing complex searches and filtering of information.
Frequently Asked Questions (FAQs)
Q1: Is 1 x 1 = 0 ever true in standard mathematics?
A1: No, in standard arithmetic, 1 multiplied by 1 always equals 1. The equation 1 x 1 = 0 is only valid within the context of Boolean algebra and specific logic operations like XOR, where 1 and 0 represent logical states, not numerical values.
Q2: What's the practical significance of understanding Boolean algebra?
A2: Understanding Boolean algebra is crucial for anyone working in computer science, electrical engineering, or any field involving digital systems. It's essential for designing and understanding how digital circuits, computers, and programming languages function at their most fundamental level.
Q3: Can other mathematical operations be defined within Boolean algebra?
A3: Yes. While AND, OR, and NOT are the most fundamental, other Boolean operations can be derived from these using combinations of gates or algebraic manipulations. These include NAND (NOT AND), NOR (NOT OR), XNOR (exclusive NOR), and many more. Each offers a unique logical function that can be leveraged in circuit design and logical reasoning.
Q4: How do I learn more about Boolean algebra?
A4: Numerous resources are available for learning Boolean algebra. Textbooks on digital logic design, online courses, and tutorials offer in-depth explanations and practical exercises to build your understanding. Many universities offer introductory courses in digital logic as part of computer science or electrical engineering curricula. Start with the fundamentals of logic gates and truth tables, then move on to more advanced concepts like Karnaugh maps for circuit simplification.
Conclusion
While counterintuitive at first glance, the equation 1 x 1 = 0 highlights the distinct nature of Boolean algebra and its profound impact on the digital world. It's not a contradiction of mathematics but rather a demonstration of the power of logical operations in manipulating binary states. Understanding the context of Boolean algebra and the specific logical operations involved, particularly the XOR gate, reveals the truth behind this seemingly paradoxical statement. This understanding is paramount for anyone seeking to delve into the fascinating world of digital systems, computer science, and the underlying logic that powers our modern technological landscape. Mastering Boolean algebra opens doors to understanding the fundamental building blocks of the digital world, from the simplest logic gate to the most complex computer system.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 X 1 0 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.