1 X 2 Y 2
monicres
Sep 10, 2025 · 6 min read
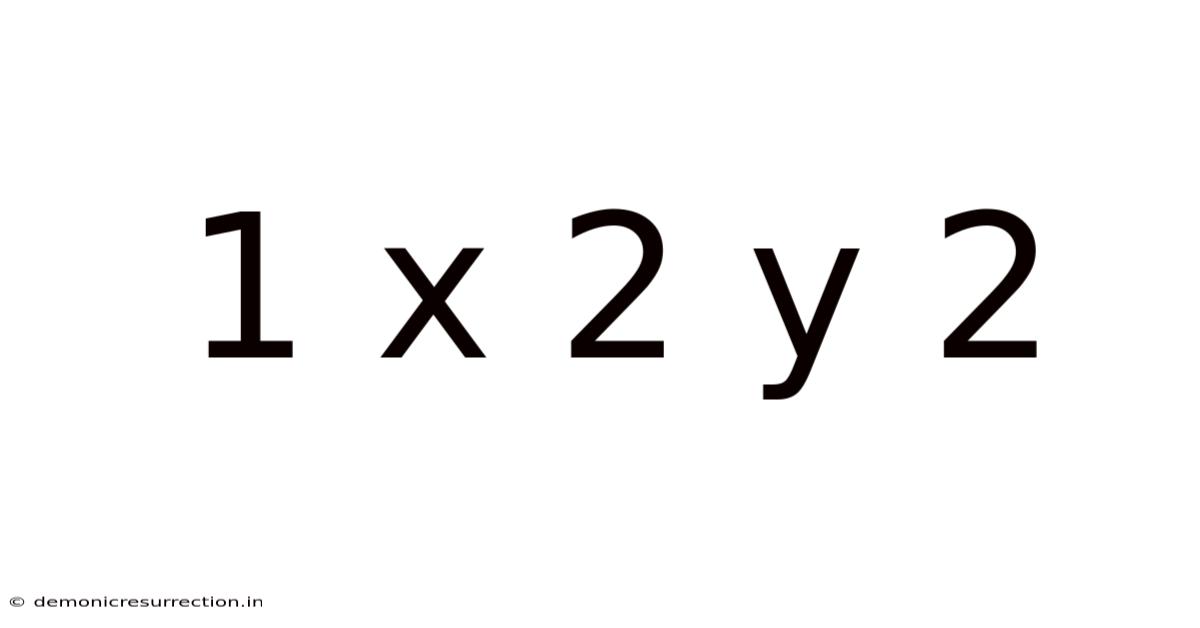
Table of Contents
Decoding the Mysterious "1 x 2y²": A Deep Dive into Quadratic Equations and Their Applications
The seemingly simple expression "1 x 2y²" might initially appear straightforward, but it opens a door to a fascinating world of mathematics, specifically the realm of quadratic equations. This article will explore this expression, delving into its meaning, its relationship to broader mathematical concepts, and its surprising applications in various fields. We'll break down the concepts in a way that's accessible to everyone, regardless of their mathematical background. Understanding "1 x 2y²" – or more accurately, understanding the principles behind it – is key to unlocking a deeper appreciation for how mathematics shapes our world.
Understanding the Basics: Variables and Coefficients
Before diving into the intricacies of "1 x 2y²," let's establish a foundational understanding of its components. The expression contains several key elements:
-
Variables: These are symbols, usually letters like 'x' and 'y', that represent unknown quantities. In our expression, 'x' and 'y' are variables.
-
Coefficients: These are the numbers that multiply the variables. In "1 x 2y²," the coefficient of 'x' is 1, and the coefficient of 'y²' is 2. While the '1' is often omitted (as in simply writing 'x'), it's crucial to remember it's implicitly there.
-
Exponents: These indicate the power to which a variable is raised. In "2y²," the exponent is 2, meaning 'y' is multiplied by itself (y * y).
Therefore, "1 x 2y²" can be more clearly written as x + 2y². This demonstrates a simple algebraic expression, specifically a polynomial because it involves multiple terms separated by addition or subtraction.
Quadratic Equations: The Heart of the Matter
The expression "x + 2y²" doesn't form a complete equation on its own. An equation requires an equals sign (=), establishing a relationship between two expressions. However, it hints at the structure of a quadratic equation.
A quadratic equation is an equation of the second degree, meaning the highest power of any variable is 2. A general form of a quadratic equation in one variable is:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants (numbers), and 'x' is the variable.
Our expression, while involving two variables, relates to quadratic equations because of the 'y²' term. If we were to set 'x + 2y²' equal to a constant, for example:
x + 2y² = 5
we would have a quadratic equation in terms of 'y' if we consider 'x' to be a constant. We can solve for 'y' using the quadratic formula or other methods such as factoring or completing the square. This shows how our simple expression is deeply connected to this important class of equations.
Similarly, if we consider 'y' as a constant, the equation becomes linear in 'x'. This illustrates the versatility of the expression and its relationship to different types of equations depending on which variables are treated as constants.
Solving Quadratic Equations: Methods and Techniques
Solving quadratic equations is a fundamental skill in algebra. Several techniques exist:
-
Factoring: This involves expressing the quadratic expression as a product of two linear expressions. For example, x² + 5x + 6 can be factored as (x + 2)(x + 3) = 0, leading to solutions x = -2 and x = -3. This method is only applicable to easily factorable quadratic equations.
-
Completing the Square: This technique involves manipulating the equation to create a perfect square trinomial, allowing for easy extraction of the square root and solving for the variable. This is a more general method applicable to all quadratic equations.
-
Quadratic Formula: This formula provides a direct solution to any quadratic equation, regardless of its factorability:
x = [-b ± √(b² - 4ac)] / 2a
This is the most versatile method, guaranteeing a solution even when factoring is difficult or impossible.
Applications of Quadratic Equations: From Physics to Finance
The seemingly abstract world of quadratic equations finds remarkably practical applications in various fields:
-
Physics: Projectile motion, the path of a thrown object, is described by a quadratic equation. Understanding quadratic equations is crucial for calculating the trajectory, maximum height, and range of projectiles.
-
Engineering: Designers and engineers use quadratic equations extensively in structural analysis, calculating stress and strain on materials, and optimizing designs for strength and stability.
-
Finance: Compound interest calculations often involve quadratic equations. Determining investment growth or loan repayments may require solving quadratic equations to find the unknown time or principal amount.
-
Computer Graphics: Quadratic curves are widely used in computer graphics to model smooth, curved shapes. They form the basis for many sophisticated visual effects and animations.
-
Economics: Quadratic functions can model cost, revenue, and profit relationships in economic models, allowing economists to analyze production levels and market equilibrium.
Extending the Concepts: Multivariable Quadratic Equations
Our initial expression, x + 2y², hints at a larger world of multivariable quadratic equations. These involve multiple variables, each possibly raised to the power of 2 or less. For instance:
x² + 2xy + y² = 10
This equation involves both 'x' and 'y' and their interaction. Solving these equations typically requires more advanced techniques, often involving systems of equations or matrix algebra. Understanding these advanced equations is critical in diverse fields like:
-
Statistical Analysis: Multivariable quadratic functions are used in regression models to examine relationships between multiple variables.
-
Machine Learning: Quadratic functions are crucial building blocks in machine learning algorithms for modeling complex data patterns.
Frequently Asked Questions (FAQ)
Q: What is the difference between a linear equation and a quadratic equation?
A: A linear equation has a degree of 1, meaning the highest power of the variable is 1 (e.g., y = 2x + 5). A quadratic equation has a degree of 2, meaning the highest power of the variable is 2 (e.g., y = x² + 3x + 2). Linear equations represent straight lines when graphed, while quadratic equations represent parabolas.
Q: Can a quadratic equation have more than two solutions?
A: No, a quadratic equation in one variable can have at most two real solutions, although it can also have complex solutions (involving imaginary numbers) or only one repeated solution (when the discriminant, b² - 4ac, is equal to zero).
Q: How do I choose the best method for solving a quadratic equation?
A: Factoring is the easiest if the equation is easily factorable. Completing the square is a reliable method, but can be more tedious. The quadratic formula is the most versatile and guarantees a solution but may involve more computation.
Q: What if the coefficient 'a' in the quadratic formula is 0?
A: If 'a' is 0, the equation is no longer quadratic; it becomes a linear equation, and the quadratic formula is not applicable.
Conclusion: The Enduring Power of Quadratic Equations
The seemingly simple expression "1 x 2y²" serves as a gateway to a rich mathematical landscape. Understanding quadratic equations and their solutions is not merely an academic exercise; it's a crucial skill with far-reaching implications in science, engineering, finance, and many other fields. Whether you're calculating the trajectory of a rocket, modeling economic growth, or designing a bridge, a solid grasp of quadratic equations provides the foundation for solving complex real-world problems. This journey into the heart of quadratic equations demonstrates the power of mathematics to illuminate the hidden structure and predictable behavior within seemingly chaotic systems. It's a testament to the elegance and utility of mathematical principles in understanding and shaping our world.
Latest Posts
Latest Posts
-
8 Rs Of Medication Administration
Sep 10, 2025
-
What Is 15 Of 80
Sep 10, 2025
-
Endings For A Formal Letter
Sep 10, 2025
-
Mi Hr To Ft S
Sep 10, 2025
-
What Is 5 Of 200000
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.