10 Of 2000 Is What
monicres
Sep 11, 2025 · 5 min read
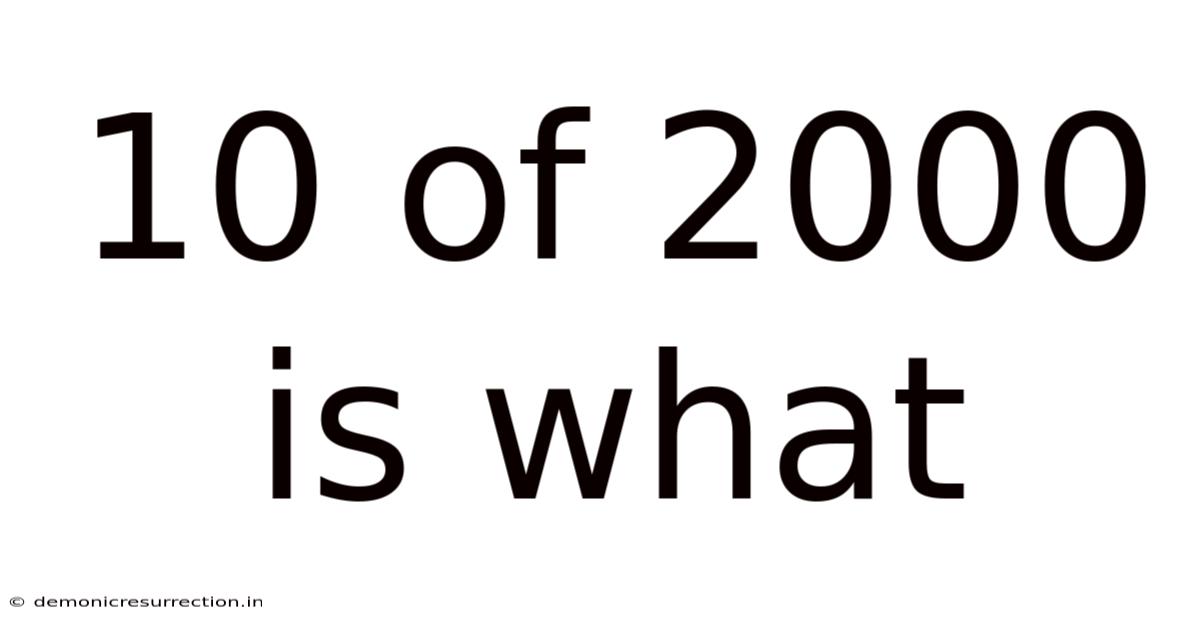
Table of Contents
10 out of 2000: Understanding Percentages and Proportions
This article explores the question: "10 out of 2000 is what?" We'll delve into the calculation, explain the underlying principles of percentages and proportions, and show you how to apply this knowledge to various situations. Understanding these concepts is crucial in many areas, from everyday life to complex scientific calculations. We'll also look at how to express this ratio in different ways and consider the significance of the result in various contexts.
Understanding Ratios and Proportions
Before we dive into the calculation, let's solidify our understanding of ratios and proportions. A ratio is a comparison of two quantities. It shows the relative size of one quantity compared to another. We can express a ratio in several ways:
- Using the colon symbol: 10:2000
- Using the word "to": 10 to 2000
- As a fraction: 10/2000
A proportion is a statement that two ratios are equal. Proportions are essential for solving problems where we know part of a relationship and need to find the other part.
Calculating the Percentage: Step-by-Step
To find out what 10 out of 2000 represents as a percentage, we follow these simple steps:
-
Express the ratio as a fraction: 10/2000
-
Convert the fraction to a decimal: Divide the numerator (10) by the denominator (2000): 10 ÷ 2000 = 0.005
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.005 x 100 = 0.5%
Therefore, 10 out of 2000 is 0.5%.
Different Ways to Express the Result
While 0.5% is the precise percentage, we can also express the relationship in other ways depending on the context:
- As a fraction: 1/200 (This is a simplified version of 10/2000)
- As a ratio: 1:200
- In words: "One in two hundred" or "Half a percent"
The choice of representation depends on the audience and the desired level of detail. For a general audience, "half a percent" might be more easily understandable than "0.5%".
The Significance of 0.5%
The significance of 0.5% depends entirely on the context. In some situations, it might be considered insignificant, while in others, it could be incredibly crucial.
-
Example 1: Manufacturing Defects: If 10 out of 2000 manufactured parts are defective, 0.5% might seem small. However, if these parts are critical components in a safety-critical system (like a car's braking system), even a small defect rate could have severe consequences.
-
Example 2: Election Results: In a close election with thousands of votes, a 0.5% difference could be enough to determine the winner. This small margin would carry significant weight.
-
Example 3: Scientific Research: In scientific studies, especially those involving large sample sizes, a 0.5% change might represent a statistically significant finding.
Applying Percentage Calculations in Daily Life
Understanding percentage calculations is invaluable in everyday situations:
- Shopping: Calculating discounts, sales tax, or tips.
- Finance: Determining interest rates, loan repayments, or investment returns.
- Health: Interpreting medical statistics, such as the effectiveness of a treatment.
- Cooking: Adjusting recipes based on the number of servings.
Mastering these skills helps you make informed decisions in various aspects of your life.
More Complex Scenarios: Proportions and Ratios
The "10 out of 2000" problem introduces the concept of proportions. Let's expand on this by considering some more complex scenarios:
Scenario 1: Scaling up the problem
What if we had 10,000 items, and the defective rate remained consistent? We can use proportions to solve this:
- We know that 10 out of 2000 is 0.5%.
- We want to find out how many would be defective in 10,000.
Let 'x' be the number of defective items in 10,000. We set up the proportion:
10/2000 = x/10000
Solving for x:
x = (10/2000) * 10000 = 50
Therefore, we would expect 50 defective items out of 10,000, maintaining the 0.5% defect rate.
Scenario 2: Finding the total number given a percentage
Let's say 0.5% of a certain population is 10 people. What is the total population size?
Let 'y' represent the total population. We set up the proportion:
10/y = 0.5/100
Solving for y:
y = (10 * 100) / 0.5 = 2000
This confirms that our initial problem of 10 out of 2000 indeed represents 0.5%.
Explanation using Scientific Notation
For very large or very small numbers, scientific notation provides a concise and efficient way to represent values. We can express 2000 as 2 x 10³. Then, 10/2000 becomes:
10 / (2 x 10³) = 5 x 10⁻³
This is equivalent to 0.005, which, when multiplied by 100, gives us 0.5%.
Frequently Asked Questions (FAQs)
Q1: How do I calculate percentages quickly without a calculator?
For quick estimations, you can use mental math techniques. Remember that 1% of a number is that number divided by 100. Then, you can approximate other percentages based on this. For example, 5% is five times 1%, and 10% is ten times 1%.
Q2: Are there any online tools or calculators for percentage calculations?
Yes, numerous online percentage calculators are available. These tools can help you quickly calculate percentages, proportions, and related calculations.
Q3: Why is it important to understand percentages and proportions?
Understanding percentages and proportions is crucial for interpreting data, making informed decisions, and solving problems in various fields. It is a fundamental skill with widespread applications.
Q4: What if the numbers aren't whole numbers?
The same principles apply. You would still express the ratio as a fraction, convert to a decimal, and then multiply by 100 to find the percentage.
Conclusion
Determining that 10 out of 2000 represents 0.5% is a straightforward calculation involving basic arithmetic and an understanding of ratios and proportions. However, the significance of this 0.5% is highly context-dependent. This seemingly simple calculation forms the foundation of many more complex mathematical and statistical applications. By grasping the underlying principles, we can confidently tackle various percentage and proportion problems encountered in daily life, academic studies, and professional endeavors. Remember to always consider the context when interpreting the results to gain a complete understanding of the data. The ability to perform these calculations accurately and efficiently is a valuable skill for personal and professional success.
Latest Posts
Latest Posts
-
The Boy Who Harry Potter
Sep 11, 2025
-
Convert 175 F To C
Sep 11, 2025
-
How To Calculate Isoelectric Point
Sep 11, 2025
-
Average Size Of A Penny
Sep 11, 2025
-
Is Tom Cruise A Scientologist
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 2000 Is What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.