2 2 X 3 3
monicres
Sep 13, 2025 · 6 min read
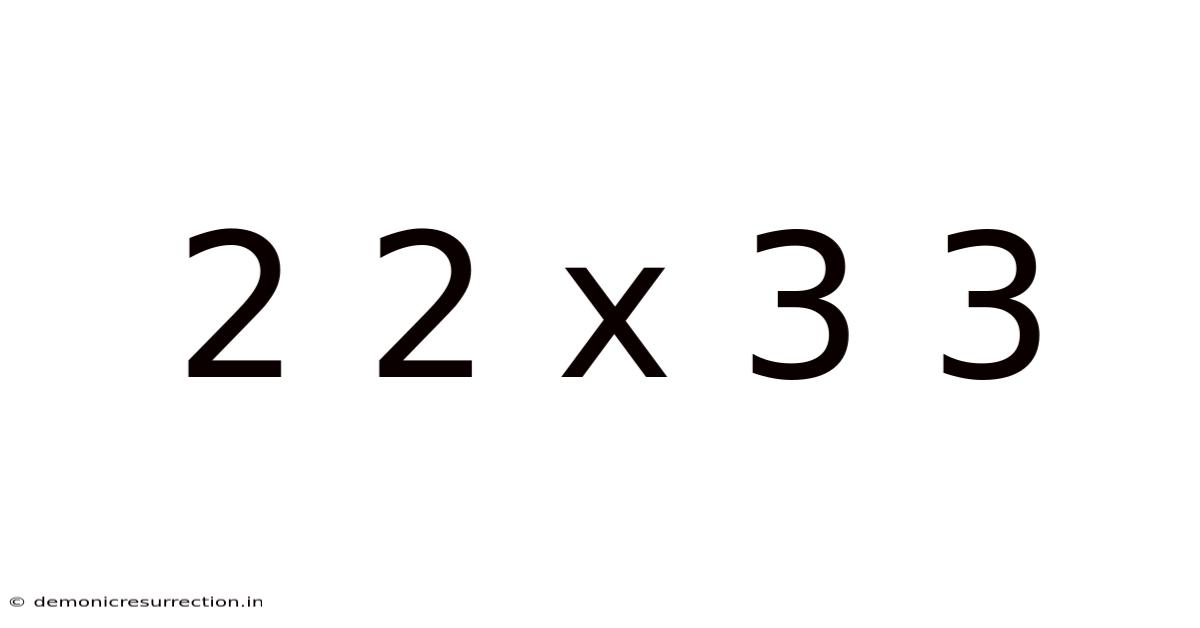
Table of Contents
Decoding 2 x 2 x 3 x 3: A Deep Dive into Multiplication, Factorization, and Beyond
This article explores the seemingly simple mathematical expression "2 x 2 x 3 x 3," delving far beyond the basic calculation to uncover its underlying mathematical principles, applications, and connections to broader concepts. We'll unpack its significance in multiplication, delve into prime factorization, examine its role in geometry and algebra, and even touch upon its relevance in more advanced mathematical fields. Understanding this seemingly straightforward equation opens doors to a richer appreciation of mathematics' elegance and interconnectedness.
Understanding the Basics: Multiplication and its Properties
At its core, "2 x 2 x 3 x 3" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that involves repeated addition. In this case, we are repeatedly adding the number 2 to itself twice (2 x 2 = 4), and then the number 3 to itself twice (3 x 3 = 9). Finally, we multiply these results: 4 x 9 = 36. This seemingly straightforward calculation highlights several key properties of multiplication:
- Commutative Property: The order of multiplication doesn't matter. We could calculate this as 2 x 3 x 2 x 3, 3 x 2 x 3 x 2, or any other permutation, and still arrive at the same answer, 36.
- Associative Property: We can group the numbers in any way we like. (2 x 2) x (3 x 3) = 4 x 9 = 36, or 2 x (2 x 3) x 3 = 2 x 6 x 3 = 36. The result remains consistent.
- Distributive Property: This property links multiplication and addition. It's less directly applicable to this specific expression, but it’s crucial for understanding more complex scenarios. For example, if we had 2 x (2 + 3), we could distribute the 2 to get (2 x 2) + (2 x 3) = 4 + 6 = 10.
These properties are fundamental building blocks in algebra and are essential for solving more complex equations.
Prime Factorization: Unveiling the Building Blocks
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). The prime factorization of 36 is 2 x 2 x 3 x 3, or, more concisely, 2² x 3². This representation is unique to every number (Fundamental Theorem of Arithmetic) and provides valuable insights.
Why is prime factorization important? It simplifies calculations, particularly in fractions and simplifying algebraic expressions. It's also crucial in cryptography, where large numbers are factored to secure data.
Applications in Geometry: Area and Volume
The expression "2 x 2 x 3 x 3" can easily be visualized geometrically.
-
Area: Imagine a rectangle with sides of length 2 and 3 units. Its area is 2 x 3 = 6 square units. Now, consider two such rectangles placed side-by-side. The combined area would be 2 x 3 x 2 = 12 square units. Alternatively, a square with sides of length 6 units has an area of 6 x 6 = 36 square units.
-
Volume: Consider a rectangular prism (a box) with dimensions 2 x 2 x 3. Its volume is 2 x 2 x 3 = 12 cubic units. If we stack two such prisms together to create a prism with dimensions 2 x 2 x 6, the volume becomes 2 x 2 x 6 = 24 cubic units. However, a cube with a side length of 3 has a volume of 3 x 3 x 3 = 27 cubic units, which is not directly related to our initial expression. But it showcases how the factors build upon each other geometrically. The total volume of two 2x2x3 prisms and one 3x3x3 cube would give a total volume much larger than 36.
Algebra and Beyond: Expanding the Horizons
Moving beyond basic arithmetic, the concept embedded in "2 x 2 x 3 x 3" plays a role in various algebraic concepts.
-
Exponents and Powers: The expression is readily expressed using exponents: 2² x 3². This notation significantly simplifies the expression and is crucial for handling larger numbers and more complex equations. The concept of exponents extends into more advanced math, such as calculus and complex numbers.
-
Polynomial Expressions: Consider a polynomial like (2x + 3)(2x + 3). Expanding this expression using the distributive property (often called FOIL – First, Outer, Inner, Last), we get 4x² + 12x + 9. This illustrates how our simple multiplication can form the foundation of more complex algebraic structures.
-
Number Theory: The prime factorization of 36 (2² x 3²) has applications in number theory, particularly in the study of divisibility, congruences, and other advanced topics. For example, determining how many divisors 36 has directly relates to its prime factorization. Since the prime factorization is 2² x 3², the number of divisors is (2+1)(2+1) = 9, because each prime factor can contribute either 0, 1 or 2 times.
Connecting the Dots: Number Patterns and Sequences
The number 36, the product of 2 x 2 x 3 x 3, appears in various number patterns and sequences. It's a perfect square (6 x 6), and it's also a triangular number (sum of integers from 1 to 8: 1+2+3+4+5+6+7+8 = 36). These connections highlight the surprising interrelationships between numbers and the intricate patterns embedded within the mathematical landscape. Exploring these patterns can be a fun way to improve mathematical intuition and problem-solving abilities.
Expanding the Scope: Higher Dimensions and Abstract Algebra
While we've explored two and three dimensions, the principles extend to higher dimensions. Imagine a four-dimensional hypercube – the volume analogy would be even more complex to visualize, but the multiplicative principles remain the same. Moreover, the concepts of prime factorization and group theory (a branch of abstract algebra) build upon these elementary ideas, establishing a deeper mathematical framework.
Frequently Asked Questions (FAQ)
Q: What is the most efficient way to calculate 2 x 2 x 3 x 3?
A: While you can multiply sequentially (2 x 2 = 4, 4 x 3 = 12, 12 x 3 = 36), the most efficient way is to recognize that 2 x 2 = 4 and 3 x 3 = 9, then multiply 4 x 9 = 36. This utilizes the associative property of multiplication.
Q: Are there any real-world applications of this calculation?
A: While this specific calculation might not have a direct, obvious real-world application, the underlying principles (multiplication, prime factorization, exponents) are crucial across many fields, including engineering (calculating area, volume, quantities), computer science (algorithms, cryptography), and finance (compound interest).
Q: How can I use this to improve my mathematical skills?
A: Practice calculations like this to solidify your understanding of basic operations. Explore prime factorization, work with exponents, and try to visualize geometric applications. The more you connect abstract concepts to concrete examples, the stronger your understanding will become.
Conclusion: The Power of Simplicity
The simple expression "2 x 2 x 3 x 3" appears elementary at first glance, but its exploration reveals layers of mathematical depth and connection. From the basic operations of multiplication to the more advanced concepts of prime factorization, exponents, and geometric applications, this unassuming equation serves as a gateway to a profound understanding of mathematical principles. By understanding its intricacies, we begin to appreciate the elegant interconnectedness of mathematics and its profound influence on various aspects of our world. Remember that even the simplest concepts can lead to the most profound insights. Continue exploring, questioning, and connecting – the mathematical journey is a lifelong adventure.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 2 X 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.