28 Out Of 35 Percentage
monicres
Sep 17, 2025 · 5 min read
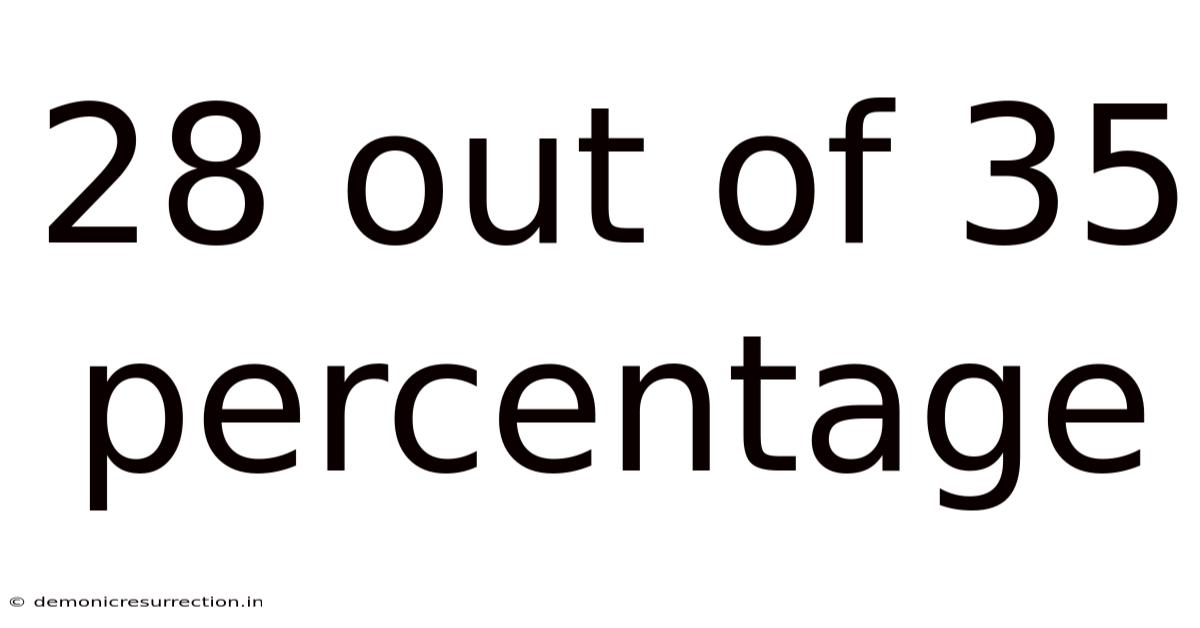
Table of Contents
Understanding 28 out of 35: Percentage, Ratio, and Practical Applications
What does 28 out of 35 actually mean? This seemingly simple question opens the door to a deeper understanding of percentages, ratios, and their real-world applications. This article will explore how to calculate this specific fraction as a percentage, delve into the underlying mathematical principles, and examine scenarios where this type of calculation is crucial. We'll also address common misconceptions and answer frequently asked questions. Whether you're a student grappling with math homework or a professional needing to analyze data, understanding the significance of 28 out of 35 will prove invaluable.
Calculating the Percentage: A Step-by-Step Guide
The core of this question lies in converting the fraction 28/35 into a percentage. A percentage represents a fraction out of 100. Here's how we do it:
-
Set up the fraction: We begin with the fraction 28/35. This represents 28 parts out of a total of 35 parts.
-
Convert to a decimal: Divide the numerator (28) by the denominator (35): 28 ÷ 35 = 0.8
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.8 x 100 = 80%
Therefore, 28 out of 35 is equal to 80%.
Understanding Ratios and Proportions
Beyond the percentage calculation, understanding the underlying ratio is crucial. A ratio is a comparison between two quantities. In this case, the ratio is 28:35. This ratio can be simplified by finding the greatest common divisor (GCD) of 28 and 35, which is 7. Dividing both numbers by 7 simplifies the ratio to 4:5. This means that for every 4 parts of one quantity, there are 5 parts of another.
This concept of proportion is fundamental in various fields. If we know that 4 out of 5 items are of a certain type, and we have a larger sample size, we can use this ratio to predict the number of items of that type in the larger sample. For instance, if we have 100 items, we can set up a proportion:
4/5 = x/100
Solving for x:
x = (4/5) * 100 = 80
This shows that if the ratio remains consistent, we would expect 80 items out of 100 to be of the same type.
Real-World Applications: Where This Calculation Matters
The calculation of 28 out of 35, and the underlying concepts of percentages and ratios, find applications in numerous areas:
-
Academics: Imagine a student answering 28 questions correctly out of a total of 35 questions on an exam. Their score is 80%, a crucial metric for assessing their understanding.
-
Business and Finance: In business, this type of calculation might represent sales figures, market share, or the success rate of a marketing campaign. A company might analyze that 28 out of 35 potential clients converted into paying customers, indicating an 80% conversion rate.
-
Science and Research: Scientists frequently use percentages and ratios to analyze experimental data. For example, a researcher might observe that 28 out of 35 lab mice responded positively to a new treatment.
-
Everyday Life: Even simple everyday tasks involve percentages and ratios. Consider calculating discounts, figuring out tips at restaurants, or determining the percentage of a task completed.
-
Sports Statistics: In sports, statistics are heavily reliant on percentages and ratios. A basketball player's free-throw percentage, a baseball player's batting average, or a football quarterback's completion percentage are all examples of this.
Beyond the Numbers: Interpreting the Results
While calculating the percentage is straightforward, the interpretation of the result is equally important. An 80% score, for instance, signifies a strong performance, but the context is crucial. In an exam with easy questions, 80% might not be exceptional, while in a particularly challenging exam, it might represent an outstanding achievement.
Similarly, in business, an 80% conversion rate could be considered excellent, especially in a competitive market. However, if the target was 95%, it might indicate areas needing improvement. The interpretation of the percentage should always be relative to the context and the expected outcome.
Addressing Common Misconceptions
Several misconceptions surround percentage calculations:
-
Confusing percentages with raw numbers: Focusing solely on the number 28 without considering the total of 35 provides an incomplete picture. It's crucial to compare the part to the whole to gain meaningful insights.
-
Improper simplification of ratios: Always simplify ratios to their simplest form. This makes comparisons easier and prevents potential errors in calculations.
-
Incorrect application of percentages: Understanding the context is key. Applying a percentage from one situation to another without considering the underlying factors can lead to erroneous conclusions.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage from a different fraction? A: Follow the same three steps outlined earlier: 1. Set up the fraction; 2. Convert to a decimal; 3. Convert the decimal to a percentage by multiplying by 100.
-
Q: What if the denominator is zero? A: You cannot divide by zero. A zero denominator indicates an undefined situation.
-
Q: Can I express the ratio 28:35 as a decimal? A: Yes, the ratio 28:35 is equivalent to the decimal 0.8.
Conclusion: Mastering the Fundamentals
Understanding the meaning of 28 out of 35, and the broader concepts of percentages and ratios, is essential for navigating various aspects of life, from academic pursuits to professional endeavors. By mastering these fundamental mathematical principles and applying them thoughtfully, individuals can gain a clearer understanding of data, make informed decisions, and enhance their problem-solving abilities. Remember that the numerical result is only half the story; the context and the interpretation of the data are equally vital. Continuous practice and application will solidify your understanding and improve your confidence in tackling similar calculations in the future. The ability to confidently interpret and apply percentages and ratios will undoubtedly serve you well in many aspects of your life.
Latest Posts
Latest Posts
-
What Is A Quantitative Property
Sep 17, 2025
-
Organ Picture Of Human Body
Sep 17, 2025
-
A And A Department Store
Sep 17, 2025
-
French Words Beginning With C
Sep 17, 2025
-
Five Words To Describe Yourself
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 28 Out Of 35 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.