3 8 As A Percent
monicres
Sep 10, 2025 · 5 min read
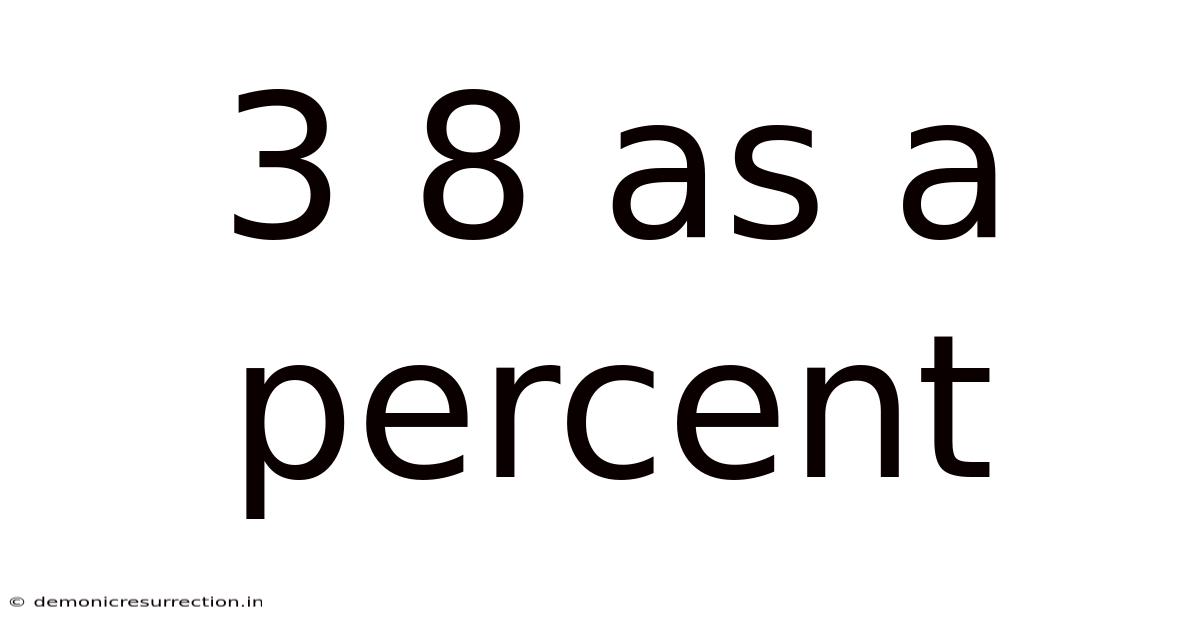
Table of Contents
Understanding 3/8 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the conversion of the fraction 3/8 into a percentage, explaining the process step-by-step, providing context, and exploring related concepts. We will cover the mathematical principles involved, offer practical examples, and address frequently asked questions. This will equip you with a solid understanding of not just 3/8 as a percentage, but also the broader concept of fraction-to-percentage conversions.
Introduction: Fractions, Decimals, and Percentages – A Unified Concept
Before diving into the specifics of converting 3/8, let's clarify the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For instance, 3/8 means 3 parts out of a total of 8 equal parts.
-
Decimals: Represent parts of a whole using a base-ten system. The decimal point separates the whole number from the fractional part. For example, 0.5 represents one-half (1/2).
-
Percentages: Express parts of a whole as a fraction of 100. The symbol "%" denotes "per hundred". For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
The beauty of these three systems lies in their interchangeability. We can easily convert from one to another, as we will demonstrate with 3/8.
Converting 3/8 to a Percentage: A Step-by-Step Guide
There are two primary methods to convert 3/8 to a percentage:
Method 1: Division and Multiplication
This method involves dividing the numerator by the denominator and then multiplying the result by 100%.
-
Divide the numerator by the denominator: 3 ÷ 8 = 0.375
-
Multiply the result by 100%: 0.375 × 100% = 37.5%
Therefore, 3/8 is equal to 37.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction of 3/8 that has a denominator of 100. This is achieved by finding a number that, when multiplied by 8, results in 100. While this is not directly possible with 8 (it's not a factor of 100), we can use the decimal approach as a shortcut, explained above, which implicitly does the same calculation.
Understanding the Result: 37.5% in Context
The result, 37.5%, signifies that 3/8 represents 37.5 parts out of 100 equal parts. This can be visualized in several ways: imagine a pie cut into 100 slices; 37.5 of those slices would represent the same portion as 3 out of 8 slices in a pie cut into 8 equal slices.
Let's look at some real-world examples to solidify this understanding:
-
Discounts: A store offers a 3/8 discount on an item. This means you get a 37.5% discount.
-
Surveys: If 3 out of 8 people surveyed prefer a particular brand, this represents a 37.5% preference rate.
-
Progress: If you have completed 3 out of 8 tasks, you have made 37.5% progress.
Further Exploration: Working with Percentages
Converting fractions to percentages is a fundamental building block for more advanced mathematical concepts. Here are some related ideas:
-
Percentage Increase/Decrease: Calculating percentage changes is vital in many contexts, such as understanding price fluctuations, population growth, or economic indicators. Understanding the base percentage (in this case, 37.5%) is key to calculating such changes.
-
Percentage of a Number: Finding a percentage of a given number is commonly used in various calculations. For example, what is 37.5% of 200? This involves multiplying 200 by 0.375, resulting in 75.
-
Proportions and Ratios: Percentages are inherently linked to proportions and ratios. Understanding these relationships is critical for solving problems in various fields, such as chemistry, physics, and engineering.
Frequently Asked Questions (FAQ)
Q1: Why is it important to know how to convert fractions to percentages?
A1: Converting fractions to percentages allows you to express fractional values in a more universally understood and easily comparable format. Percentages are widely used in everyday life, finance, and various fields, making this conversion skill essential.
Q2: Are there other ways to convert 3/8 to a percentage?
A2: While the methods described above are the most common and straightforward, more advanced mathematical techniques could be employed, but they would generally be less efficient for this specific conversion.
Q3: Can I use a calculator for this conversion?
A3: Absolutely! Most calculators have functions that allow you to perform the division and multiplication steps directly, simplifying the process.
Q4: What if I have a more complex fraction?
A4: The same principles apply for converting any fraction to a percentage. Simply divide the numerator by the denominator and multiply the result by 100%. For example, to convert 5/12 to a percentage, you would perform: 5 ÷ 12 = 0.41666... and then 0.41666... × 100% ≈ 41.67%.
Conclusion: Mastering Fraction-to-Percentage Conversions
Understanding how to convert fractions, such as 3/8, to percentages is a critical skill in mathematics and has wide-ranging practical applications. By mastering this conversion, you gain a more comprehensive understanding of numerical representation and develop the ability to analyze and interpret data more effectively. The methods outlined in this guide, combined with the practical examples and FAQs, should equip you to confidently tackle similar conversions and apply this knowledge to real-world problems. Remember, the key is to understand the underlying principle: percentages represent parts of a whole expressed as a fraction of 100. Once you grasp this concept, converting any fraction to a percentage becomes a straightforward task. Practice makes perfect; so, try converting other fractions to percentages to reinforce your understanding and build your confidence.
Latest Posts
Latest Posts
-
Molar Mass Of N Pentane
Sep 10, 2025
-
Food Web In A Tundra
Sep 10, 2025
-
10 Little Soldier Boys Poem
Sep 10, 2025
-
The New Great Game 2012
Sep 10, 2025
-
Synopsis Of Touching Spirit Bear
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.