5 4 As A Percent
monicres
Sep 13, 2025 · 5 min read
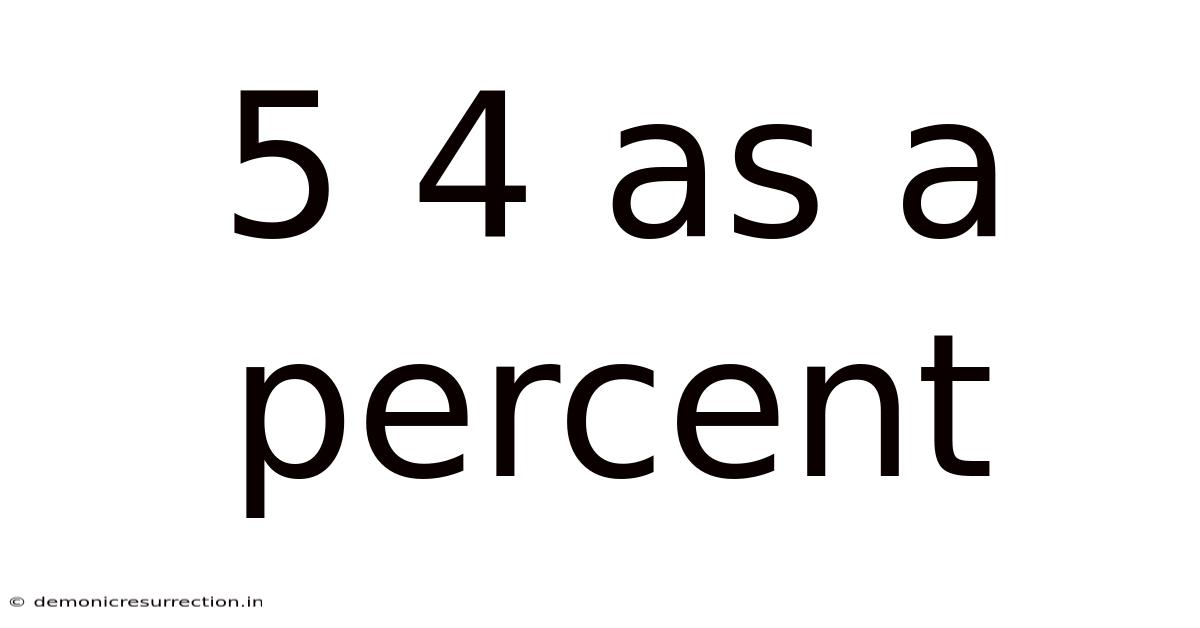
Table of Contents
Understanding 5/4 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and interest rates to understanding statistical data and expressing proportions. This article delves into the process of converting the fraction 5/4 into a percentage, explaining the steps involved, providing additional examples, and addressing frequently asked questions. We'll explore the underlying principles and ensure a complete understanding of this concept.
Understanding Fractions and Percentages
Before we tackle the conversion of 5/4 to a percentage, let's briefly review the definitions of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many parts make up the whole. For example, in the fraction 5/4, 5 is the numerator and 4 is the denominator.
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." We use the symbol "%" to represent percentages. For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Converting 5/4 to a Percentage: Step-by-Step
The conversion of 5/4 to a percentage involves two primary steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we divide 5 by 4:
5 ÷ 4 = 1.25
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. This is equivalent to moving the decimal point two places to the right.
1.25 × 100 = 125
Therefore, 1.25 as a percentage is 125%.
In summary: 5/4 = 1.25 = 125%
This means that 5/4 represents 125% of a whole. This might seem counterintuitive at first, as we are used to fractions being less than or equal to 1 (or 100%). However, an improper fraction like 5/4, where the numerator is larger than the denominator, represents a value greater than 1. This is because it signifies more than one whole unit.
Illustrative Examples: Understanding Improper Fractions and Percentages
Let's explore a few more examples to solidify our understanding of improper fractions and their percentage equivalents:
- Example 1: 7/5 as a percentage
- Convert to decimal: 7 ÷ 5 = 1.4
- Convert to percentage: 1.4 × 100 = 140%
Therefore, 7/5 = 140%
- Example 2: 9/2 as a percentage
- Convert to decimal: 9 ÷ 2 = 4.5
- Convert to percentage: 4.5 × 100 = 450%
Therefore, 9/2 = 450%
- Example 3: A real-world application
Imagine you're investing money. Your initial investment grows by 5/4 its original value. This means your investment has increased by 125% of its original amount.
These examples illustrate that percentages can exceed 100% when dealing with improper fractions, representing an increase beyond the initial value.
The Mathematical Explanation: Proportions and Ratios
The conversion from a fraction to a percentage fundamentally involves the concept of proportion. A percentage expresses a ratio relative to 100. The process we followed earlier is mathematically equivalent to setting up a proportion:
5/4 = x/100
To solve for x (the percentage), we cross-multiply:
4x = 500
x = 500/4 = 125
This confirms our earlier result that 5/4 is equal to 125%. This approach provides a more formal mathematical foundation for the conversion process.
Different Approaches to Solving the Problem
While the method above is straightforward, other approaches can be used to convert 5/4 to a percentage. For instance:
-
Converting to a mixed number: 5/4 can be expressed as the mixed number 1 ¼. This means it's one whole and one-quarter. One whole is 100%, and one-quarter is 25% (100% ÷ 4 = 25%). Adding these together, 100% + 25% = 125%.
-
Using a calculator: Most calculators have built-in functions that directly convert fractions to percentages. Simply input 5/4 and use the percentage function.
Frequently Asked Questions (FAQ)
- Q: Why can percentages be greater than 100%?
A: Percentages represent a ratio relative to a base value (often 100). If a value increases beyond the initial base value, the percentage will exceed 100%. This indicates a growth or increase beyond the original amount.
- Q: What are some real-world applications of percentages exceeding 100%?
A: Many situations involve percentages greater than 100%. Examples include: * Investment returns: An investment that doubles in value has a 200% return. * Population growth: A town whose population increases by more than its original size experiences population growth exceeding 100%. * Price increases: If a product’s price increases by more than its original cost, the price increase is represented by a percentage above 100%.
- Q: What if I have a complex fraction? How do I convert it to a percentage?
A: Simplify the complex fraction first. For example, if you have (3/4)/(1/2), simplify it to (3/4) * (2/1) = 6/4 = 3/2. Then convert 3/2 to a percentage using the steps outlined above.
- Q: How do I convert a percentage back to a fraction?
A: To convert a percentage back to a fraction, divide the percentage by 100 and simplify. For example, to convert 125% back to a fraction, divide 125 by 100 to get 1.25, then express 1.25 as a fraction which simplifies to 5/4.
Conclusion
Converting fractions to percentages is a valuable skill with broad applications. Understanding the process of converting 5/4 to 125% involves a clear, step-by-step procedure. Remember that improper fractions result in percentages greater than 100%, representing values exceeding the initial whole. By mastering this fundamental concept, you enhance your mathematical proficiency and improve your ability to interpret and apply numerical data in various contexts. This comprehensive guide provides a thorough understanding, addressing common questions and equipping you to confidently handle similar fraction-to-percentage conversions.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.