5 Percent Of 250 000
monicres
Sep 11, 2025 · 5 min read
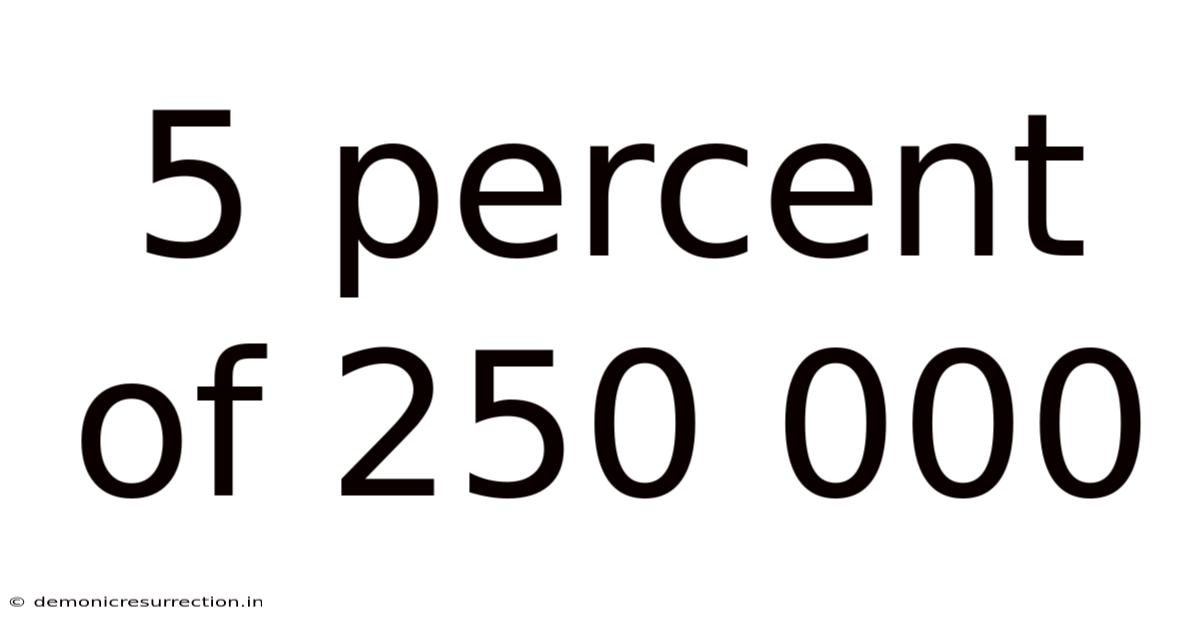
Table of Contents
Decoding 5 Percent of 250,000: A Comprehensive Guide
Finding 5% of 250,000 might seem like a simple calculation, but understanding the underlying principles behind percentages and their applications in various contexts is crucial. This article delves deep into calculating 5% of 250,000, exploring different methods, practical applications, and related concepts. We'll move beyond the simple answer to provide a robust understanding of percentages, their importance, and how to confidently tackle similar problems. This guide is suitable for anyone from students needing to brush up on their math skills to professionals needing a refresher on percentage calculations.
Understanding Percentages: The Foundation
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per hundred". So, 5% means 5 out of every 100, or 5/100, which simplifies to 1/20 as a fraction and 0.05 as a decimal. Understanding this fundamental concept is vital for accurately calculating percentages.
Calculating 5% of 250,000: Three Methods
There are several ways to calculate 5% of 250,000. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent (5% = 0.05) and then multiply it by the number:
0.05 * 250,000 = 12,500
Therefore, 5% of 250,000 is 12,500.
Method 2: Using the Fraction Equivalent
We can also use the fraction equivalent of 5% (1/20) to perform the calculation:
(1/20) * 250,000 = 250,000 / 20 = 12,500
This method demonstrates the relationship between fractions and percentages. Dividing 250,000 by 20 gives us the same result: 12,500.
Method 3: Breaking Down the Calculation
For a deeper understanding, we can break down the calculation into smaller, easier-to-manage steps. Finding 1% of 250,000 is simply dividing by 100:
250,000 / 100 = 2,500
Since 5% is five times 1%, we multiply the result by 5:
2,500 * 5 = 12,500
This method highlights the proportional relationship between percentages and the whole number. The answer, once again, is 12,500.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations isn't just about solving mathematical problems; it's about applying this knowledge to real-world situations. Here are a few examples where calculating percentages is essential:
- Finance: Calculating interest on loans, investments, or savings accounts. For example, a 5% interest rate on a $250,000 investment would yield $12,500 in interest (before considering compounding).
- Sales and Discounts: Determining the final price of an item after a discount. A 5% discount on a $250,000 property would mean a $12,500 reduction in price.
- Taxes: Calculating sales tax, income tax, or property tax. If the tax rate is 5%, then the tax amount on a $250,000 property would be $12,500.
- Statistics: Representing proportions and distributions of data. For instance, if 5% of a population of 250,000 people have a specific characteristic, that equates to 12,500 individuals.
- Business: Calculating profit margins, analyzing market share, or determining growth percentages. A 5% increase in sales of $250,000 would represent a $12,500 increase.
Expanding the Understanding: Beyond 5% of 250,000
While we've focused on 5% of 250,000, the principles discussed can be applied to any percentage and any number. Let's explore how to calculate x% of y:
The general formula is:
(x/100) * y = Result
Where 'x' represents the percentage and 'y' represents the number. This formula provides a versatile tool for solving a wide range of percentage problems.
Advanced Concepts: Percentage Increase and Decrease
Percentage calculations are not limited to finding a percentage of a number. We often need to calculate percentage increases or decreases. For example, if a $250,000 investment increases by 5%, the new value is calculated as follows:
- Calculate the increase: 0.05 * 250,000 = 12,500
- Add the increase to the original value: 250,000 + 12,500 = 262,500
Conversely, if the investment decreases by 5%:
- Calculate the decrease: 0.05 * 250,000 = 12,500
- Subtract the decrease from the original value: 250,000 - 12,500 = 237,500
Troubleshooting Common Mistakes
Even simple percentage calculations can sometimes lead to errors. Here are some common pitfalls to avoid:
- Incorrect Decimal Conversion: Ensure you correctly convert the percentage to its decimal equivalent before multiplying. For example, 5% is 0.05, not 0.5.
- Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when dealing with more complex calculations involving percentages and other mathematical operations.
- Misinterpreting the Problem: Carefully read and understand the problem statement before attempting the calculation. Make sure you're calculating the correct percentage and applying the appropriate operation (addition, subtraction, multiplication, or division).
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 5% of 250,000?
A: The easiest way is using the decimal equivalent: 0.05 * 250,000 = 12,500.
Q: Can I use a calculator for this?
A: Absolutely! Calculators are useful, especially for larger numbers or more complex calculations.
Q: How do I calculate a different percentage of 250,000?
A: Use the formula (x/100) * 250,000, replacing 'x' with the desired percentage.
Q: What if I need to calculate a percentage increase or decrease?
A: Calculate the percentage change, then add or subtract that amount from the original value.
Q: Are there any online tools to help with percentage calculations?
A: While external links are not allowed, a simple search for "percentage calculator" will provide many online resources.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a fundamental skill applicable across numerous fields. While finding 5% of 250,000 might seem straightforward, grasping the underlying concepts and methods allows for tackling more complex percentage problems with confidence. By mastering these principles, you'll be better equipped to handle financial calculations, analyze data, and solve real-world problems involving proportions and ratios. Remember to practice consistently, and you will find yourself effortlessly navigating the world of percentages.
Latest Posts
Latest Posts
-
Difference Between Serum And Plasma
Sep 11, 2025
-
Sodium A Metal Or Nonmetal
Sep 11, 2025
-
Wassily Kandinsky Yellow Red Blue
Sep 11, 2025
-
How Long Is 44 Weeks
Sep 11, 2025
-
City Of Ember Book Synopsis
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 250 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.