8 X 2 X 4
monicres
Sep 04, 2025 · 6 min read
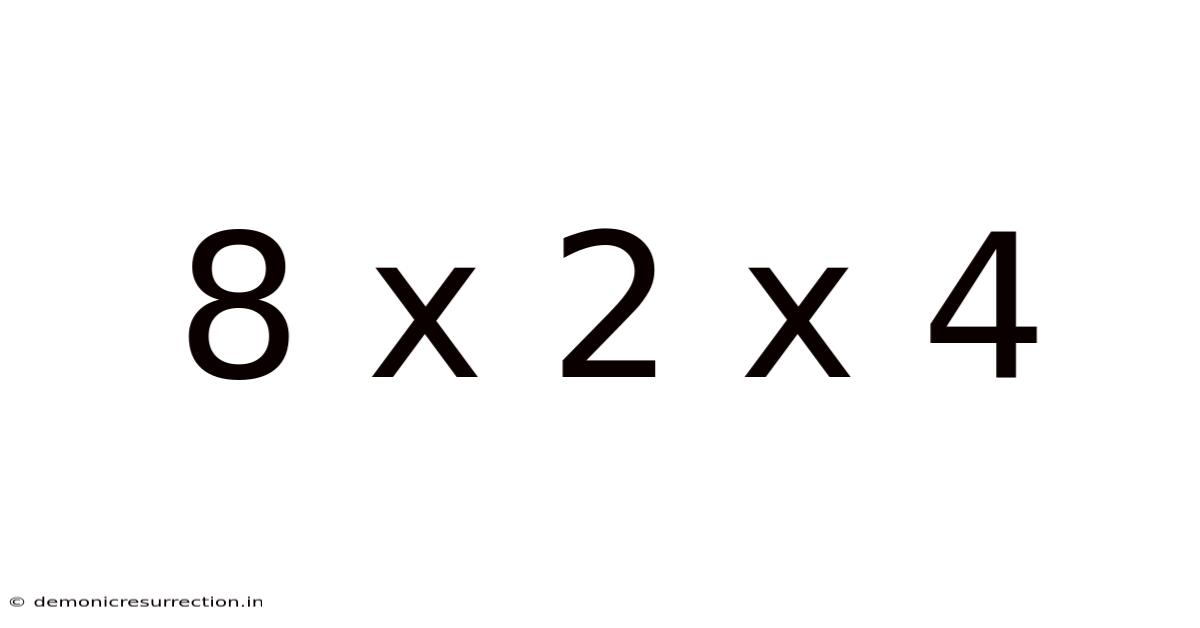
Table of Contents
Decoding 8 x 2 x 4: Exploring Dimensions, Volume, and Applications
Understanding the dimensions 8 x 2 x 4 is more than just a simple multiplication problem; it's a gateway to comprehending spatial reasoning, volume calculations, and practical applications across various fields. This seemingly straightforward set of numbers holds significance in construction, carpentry, packaging, and even theoretical geometry. This article will delve into the meaning of 8 x 2 x 4, explore its implications in different contexts, and address frequently asked questions.
Introduction: What Does 8 x 2 x 4 Represent?
The expression "8 x 2 x 4" typically represents the dimensions of a rectangular prism (or cuboid) – a three-dimensional shape with six rectangular faces. Each number signifies a length along one of the three perpendicular axes: 8 units in length, 2 units in width, and 4 units in height. These units can be anything from inches or centimeters to meters or even kilometers, depending on the context. The key is understanding the relative proportions of these three dimensions and how they influence the object's overall properties. We will explore these properties and applications in detail.
Calculating Volume: The Cubic Measurement
One of the most fundamental calculations involving these dimensions is determining the volume of the rectangular prism. The volume represents the three-dimensional space enclosed within the object's boundaries. It's calculated by multiplying the three dimensions together:
Volume = Length x Width x Height = 8 x 2 x 4 = 64 cubic units
This means that the rectangular prism with dimensions 8 x 2 x 4 encloses a space equivalent to 64 cubes, each with sides of one unit in length. The units of volume will be cubic units (e.g., cubic inches, cubic centimeters, cubic meters). This seemingly simple calculation is crucial in various real-world applications, from estimating the amount of material needed for a construction project to determining the capacity of a container.
Surface Area Calculation: Understanding the Exterior
While volume focuses on the space inside the object, the surface area refers to the total area of all its external faces. Calculating the surface area of a rectangular prism requires a slightly more complex approach:
- Area of the top and bottom faces: 8 x 4 = 32 square units each. Total: 64 square units
- Area of the front and back faces: 8 x 2 = 16 square units each. Total: 32 square units
- Area of the left and right faces: 4 x 2 = 8 square units each. Total: 16 square units
Total surface area = 64 + 32 + 16 = 112 square units
Understanding the surface area is important in various applications, such as determining the amount of paint needed to cover a surface or calculating the material required for packaging.
Practical Applications: Where Do We See 8 x 2 x 4?
The dimensions 8 x 2 x 4, or variations thereof, appear frequently in various real-world scenarios. Here are some examples:
-
Construction and Carpentry: Lumber is often cut and sold in standard sizes. A piece of lumber with dimensions close to 8 x 2 x 4 (inches or centimeters) might be a common size used for framing, supports, or other structural elements. Understanding these dimensions is essential for accurate planning and efficient material usage.
-
Packaging and Shipping: Boxes and containers are designed to optimize space and protect their contents. A box with dimensions close to 8 x 2 x 4 might be used for packaging various goods, from smaller electronic components to books or other items. The volume and surface area calculations are crucial for determining shipping costs and optimizing storage space.
-
Engineering and Design: Engineers and designers frequently encounter rectangular prisms in their work. Whether designing buildings, machines, or other structures, understanding the relationships between dimensions, volume, and surface area is essential for creating functional and efficient designs.
-
Theoretical Geometry and Mathematics: The rectangular prism with dimensions 8 x 2 x 4 serves as a simple yet powerful example for teaching concepts in geometry, including volume calculations, surface area computations, and spatial reasoning. It's a fundamental building block for understanding more complex geometric shapes and spatial relationships.
Variations and Scalability: Adapting to Different Contexts
It's important to note that the numbers 8, 2, and 4 represent relative proportions. The actual units can vary greatly depending on the context. For instance:
- 8 x 2 x 4 inches: This might represent a small wooden block or a component in a machine.
- 8 x 2 x 4 centimeters: This could represent a slightly larger object, possibly a box or a container.
- 8 x 2 x 4 meters: This would be significantly larger, potentially a section of a wall or a part of a larger structure.
The adaptability of these dimensions highlights their versatility and importance across various scales.
Beyond the Basics: Exploring Related Concepts
Understanding 8 x 2 x 4 opens doors to exploring more advanced concepts:
-
Scaling: What happens to the volume and surface area if we double, triple, or halve each dimension? This exploration helps in understanding the relationship between scaling and the changes in volume and surface area.
-
Optimization: How can we adjust the dimensions to maximize volume while minimizing surface area (or vice-versa)? This is a crucial aspect of design and engineering, where efficiency is paramount.
-
Different Unit Systems: Converting between different unit systems (e.g., inches to centimeters, cubic feet to cubic meters) requires a good understanding of unit conversion principles and their implications on volume and surface area calculations.
Frequently Asked Questions (FAQ)
Q: What are the units of measurement typically associated with 8 x 2 x 4 dimensions?
A: The units can vary greatly depending on the application. Common units include inches, centimeters, meters, or even feet. The context always dictates the appropriate unit.
Q: Can I use 8 x 2 x 4 to represent any rectangular prism?
A: No, 8 x 2 x 4 represents a specific set of proportions. Any rectangular prism can be described by its three dimensions (length, width, height), but those dimensions could be any combination of numbers.
Q: How does the orientation of the 8 x 2 x 4 object affect its properties?
A: The volume remains constant regardless of orientation. However, the surface area calculation might change slightly depending on which side is considered the "base." The impact of this difference is generally negligible for most practical applications.
Q: What are some real-world examples of objects with dimensions similar to 8 x 2 x 4?
A: Examples include standard-sized bricks, lumber pieces used in construction, packaging boxes for various goods, and components in machinery or electronics.
Q: How can I use this knowledge in my studies or profession?
A: Understanding volume and surface area calculations is crucial in fields like architecture, engineering, construction, packaging design, and various manufacturing processes. The concepts are also fundamental to many areas of mathematics and physics.
Conclusion: The Significance of Understanding Dimensions
The seemingly simple dimensions 8 x 2 x 4 unlock a world of understanding regarding spatial reasoning, volume calculations, and practical applications across diverse fields. From constructing buildings to designing packaging, the principles discussed in this article are fundamental for efficient and effective problem-solving. By mastering these basic concepts, one gains a valuable foundation for tackling more complex challenges in geometry, engineering, and various other disciplines. Remember that the seemingly simple act of multiplying three numbers opens a door to a wealth of practical applications and deeper understanding of the three-dimensional world around us. Continue exploring these principles, and you will find their relevance and applications far-reaching and impactful.
Latest Posts
Related Post
Thank you for visiting our website which covers about 8 X 2 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.