Cos 2 Sin 2 1
monicres
Sep 13, 2025 · 5 min read
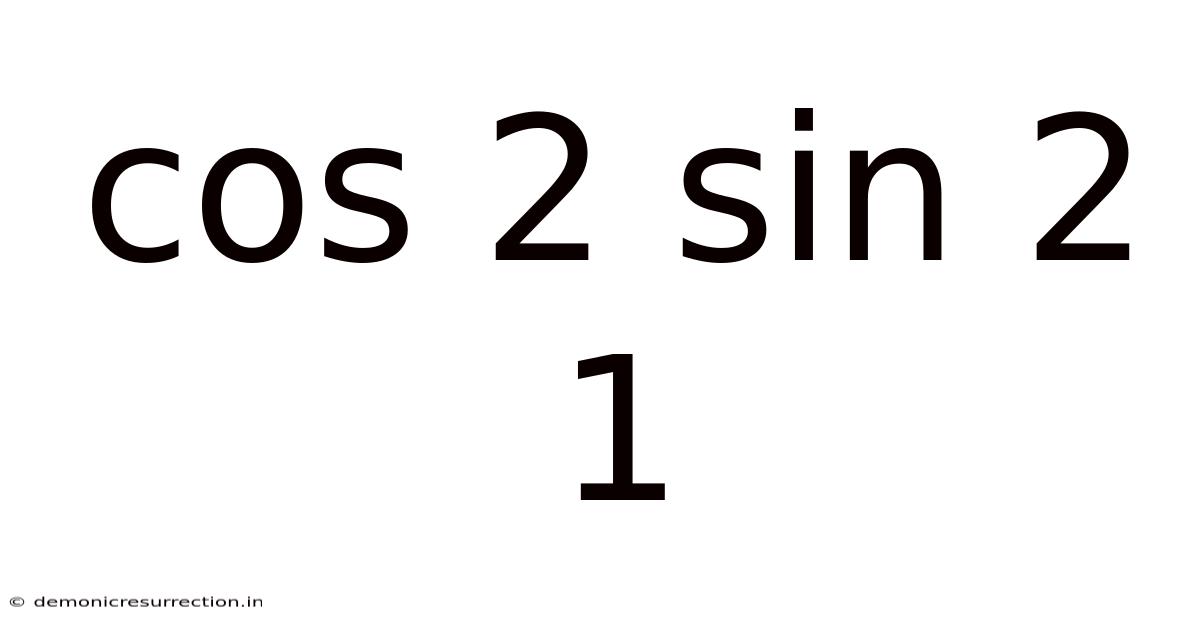
Table of Contents
It seems there's a typographical error in your request: "cos 2 sin 2 1". It's unclear what mathematical expression you intend. However, I can provide a comprehensive article exploring related trigonometric identities and concepts, assuming you intended something like exploring the relationships between cosine, sine, and their squares, potentially involving angles of 1 radian or 1 degree.
Understanding Trigonometric Identities: A Deep Dive into Cosine, Sine, and their Squares
Trigonometry, the study of triangles and their relationships, relies heavily on fundamental identities. These identities are equations that hold true for all values of the angles involved. Understanding these identities is crucial for simplifying complex expressions, solving equations, and proving other mathematical relationships. This article will explore the connections between cosine (cos), sine (sin), and their squares (cos² and sin²), focusing on applications and deeper understanding.
Introduction to Basic Trigonometric Identities
Before diving into more complex relationships, let's review some fundamental trigonometric identities:
-
Pythagorean Identity: This is arguably the most important identity in trigonometry:
cos²(θ) + sin²(θ) = 1. This identity stems directly from the Pythagorean theorem applied to a right-angled triangle where θ is one of the acute angles. The cosine of θ represents the ratio of the adjacent side to the hypotenuse, and the sine of θ represents the ratio of the opposite side to the hypotenuse. Squaring these ratios and adding them, based on the Pythagorean theorem (a² + b² = c²), results in the identity. -
Reciprocal Identities: These identities define the relationships between the primary trigonometric functions (sine, cosine, and tangent) and their reciprocals:
sec(θ) = 1/cos(θ)(secant)csc(θ) = 1/sin(θ)(cosecant)cot(θ) = 1/tan(θ)(cotangent)
-
Quotient Identities: These identities show the relationship between tangent and cotangent to sine and cosine:
tan(θ) = sin(θ)/cos(θ)(tangent)cot(θ) = cos(θ)/sin(θ)
Exploring Cosine Squared (cos²θ) and Sine Squared (sin²θ)
The squares of cosine and sine, cos²θ and sin²θ, frequently appear in various trigonometric applications. Their importance stems from their ability to simplify complex expressions and solve trigonometric equations. Here are some key aspects:
-
Double-Angle Identities: These identities express trigonometric functions of 2θ in terms of trigonometric functions of θ. They are particularly useful in calculus and solving trigonometric equations. For example:
cos(2θ) = cos²(θ) - sin²(θ) = 2cos²(θ) - 1 = 1 - 2sin²(θ)sin(2θ) = 2sin(θ)cos(θ)
Notice how these identities directly incorporate cos²θ and sin²θ. These are derived using the angle sum formulas and the Pythagorean identity.
-
Power-Reducing Identities: These identities allow us to express higher powers of sine and cosine in terms of lower powers, often simplifying integrations and calculations. They are derived from the double-angle formulas:
cos²(θ) = (1 + cos(2θ))/2sin²(θ) = (1 - cos(2θ))/2
-
Product-to-Sum Identities: These identities convert products of trigonometric functions into sums or differences. These are particularly useful in simplifying expressions involving products of sines and cosines:
cos(A)cos(B) = ½[cos(A+B) + cos(A-B)]sin(A)sin(B) = ½[cos(A-B) - cos(A+B)]sin(A)cos(B) = ½[sin(A+B) + sin(A-B)]
These identities show the interconnectedness of different trigonometric functions and their powers.
Applications in Calculus and Physics
Cosine squared and sine squared have significant applications in various fields, including:
-
Calculus: In integral calculus, power-reducing formulas are crucial for integrating functions involving higher powers of sine and cosine. This makes evaluating complex integrals considerably easier. For instance, the integral of cos⁴(x) can be significantly simplified using power-reducing identities.
-
Physics: These functions are prevalent in describing oscillatory and wave phenomena. In physics, they are used in modeling simple harmonic motion, wave propagation (sound, light), and alternating current circuits. The intensity of light or sound waves often involves expressions with cos²θ or sin²θ.
-
Engineering: Many engineering applications involve periodic functions, making trigonometric identities essential for analysis and design. For example, in signal processing, understanding these identities is critical for manipulating and analyzing signals.
Specific Case: Angles of 1 Radian and 1 Degree
While the identities discussed above apply to any angle θ, let's consider the specific cases of θ = 1 radian and θ = 1 degree:
-
1 Radian: Using a calculator, we can approximate:
cos(1 radian) ≈ 0.5403sin(1 radian) ≈ 0.8415cos²(1 radian) ≈ 0.2919sin²(1 radian) ≈ 0.7081
Notice that cos²(1 rad) + sin²(1 rad) ≈ 1, confirming the Pythagorean identity.
-
1 Degree:
cos(1 degree) ≈ 0.9998sin(1 degree) ≈ 0.0175cos²(1 degree) ≈ 0.9996sin²(1 degree) ≈ 0.0003
Again, the Pythagorean identity holds approximately true. The small difference is due to rounding errors.
Frequently Asked Questions (FAQ)
-
Q: Why are trigonometric identities important?
- A: They are fundamental to simplifying complex expressions, solving trigonometric equations, and providing a basis for numerous applications in calculus, physics, and engineering. They allow us to manipulate and transform trigonometric functions, making them easier to work with.
-
Q: How do I prove trigonometric identities?
- A: Usually, you start with one side of the equation and manipulate it using known identities (Pythagorean, reciprocal, quotient, etc.) until it matches the other side. Sometimes working with both sides simultaneously can be helpful.
-
Q: Are there other important identities besides the ones mentioned?
- A: Yes! There are numerous other identities, including sum-to-product identities, triple-angle identities, and many more. The ones presented here are some of the most frequently used.
-
Q: What is the significance of the angle being in radians or degrees?
- A: The choice depends on the context. Radians are preferred in calculus because they simplify derivative and integral formulas. Degrees are more commonly used in everyday applications and geometry. The identities themselves are true regardless of the unit used, as long as consistency is maintained.
Conclusion
Understanding trigonometric identities, especially the relationships between cosine, sine, and their squares, is crucial for anyone working with trigonometric functions. From simplifying complex expressions to solving equations and applying them to real-world problems in various fields, these identities are indispensable tools. The Pythagorean identity, double-angle formulas, and power-reducing identities are particularly essential, providing the building blocks for manipulating and simplifying trigonometric expressions. This deeper understanding not only improves mathematical problem-solving skills but also unlocks a broader understanding of periodic phenomena throughout the natural world and engineering applications. Continued exploration of these concepts will lead to a more robust comprehension of mathematics and its practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Cos 2 Sin 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.