Derivative Of Inverse Tan 2x
monicres
Sep 08, 2025 · 6 min read
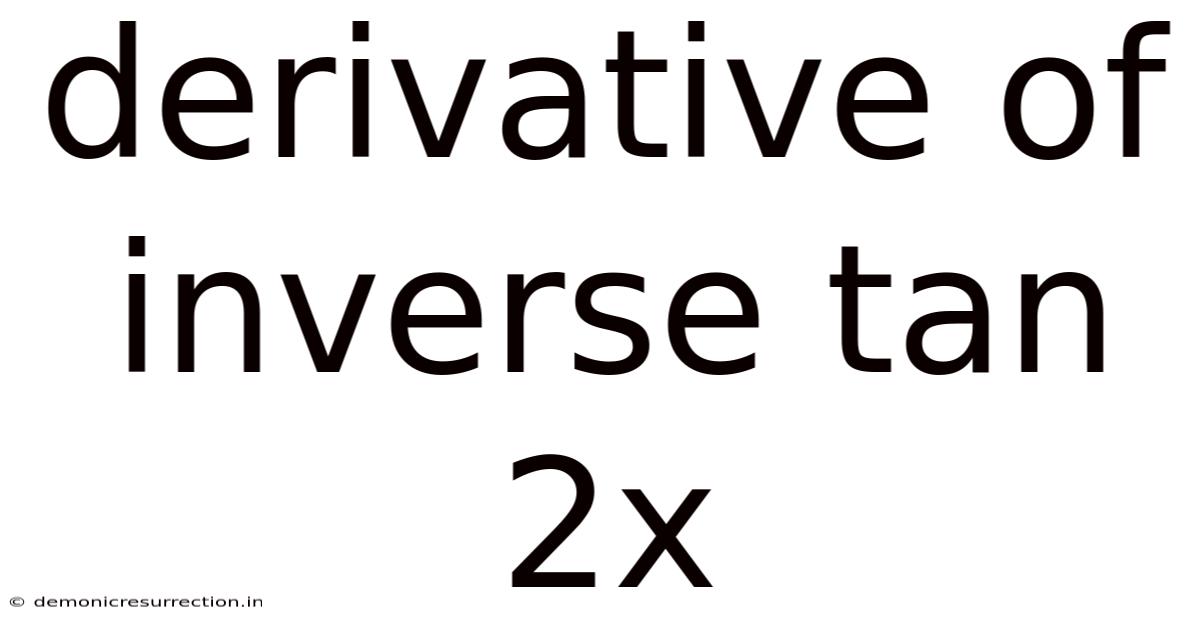
Table of Contents
Unveiling the Mystery: Deriving the Derivative of Inverse Tan 2x
Finding the derivative of inverse trigonometric functions can sometimes feel like navigating a mathematical maze. This article will illuminate the path to understanding and deriving the derivative of inverse tan 2x, a crucial concept in calculus. We'll break down the process step-by-step, offering clear explanations and exploring the underlying principles. By the end, you'll not only know the answer but also possess a deeper understanding of the techniques involved. This will equip you to tackle similar problems with confidence.
Introduction: Understanding Inverse Trigonometric Functions
Before diving into the derivative itself, let's refresh our understanding of inverse trigonometric functions. These functions, often denoted as arcsin(x), arccos(x), arctan(x), etc., are the inverses of the standard trigonometric functions (sin(x), cos(x), tan(x)). They essentially "undo" the action of their trigonometric counterparts. For example, if sin(θ) = ½, then arcsin(½) = θ (where θ is typically within a restricted range to ensure a unique output).
In our case, we're dealing with arctan(x), or the inverse tangent function. This function answers the question: "What angle has a tangent equal to x?" It's crucial to remember that the range of arctan(x) is typically restricted to (-π/2, π/2) to guarantee a single, well-defined output for each input.
The Chain Rule: A Crucial Tool
To successfully derive the derivative of inverse tan 2x, we need a powerful tool from calculus: the chain rule. The chain rule states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) multiplied by the derivative of the inner function. Mathematically, if we have a function y = f(g(x)), then its derivative is:
dy/dx = f'(g(x)) * g'(x)
Deriving the Derivative: Step-by-Step
Now, let's apply our knowledge to find the derivative of arctan(2x). We'll denote y = arctan(2x). Our goal is to find dy/dx.
Step 1: Identify the Outer and Inner Functions
In our composite function y = arctan(2x), the outer function is f(u) = arctan(u), where u represents the inner function. The inner function is g(x) = 2x.
Step 2: Find the Derivative of the Outer Function
The derivative of arctan(u) with respect to u is:
d(arctan(u))/du = 1 / (1 + u²)
Step 3: Find the Derivative of the Inner Function
The derivative of the inner function, 2x, with respect to x is straightforward:
d(2x)/dx = 2
Step 4: Apply the Chain Rule
Now we apply the chain rule:
dy/dx = d(arctan(u))/du * d(2x)/dx
Substituting the derivatives we found in steps 2 and 3, and remembering that u = 2x, we get:
dy/dx = [1 / (1 + (2x)²)] * 2
Step 5: Simplify the Result
Simplifying the expression, we arrive at the final derivative:
dy/dx = 2 / (1 + 4x²)
Therefore, the derivative of arctan(2x) with respect to x is 2 / (1 + 4x²).
A Deeper Dive: Implicit Differentiation (Alternative Approach)
While the chain rule provides a straightforward approach, we can also derive the derivative using implicit differentiation. This method offers a valuable alternative perspective.
Step 1: Start with the Definition
Let y = arctan(2x). This implies that tan(y) = 2x.
Step 2: Differentiate Implicitly
Differentiate both sides of the equation tan(y) = 2x with respect to x. Remember to use the chain rule on the left side:
sec²(y) * (dy/dx) = 2
Step 3: Solve for dy/dx
Now, isolate dy/dx:
dy/dx = 2 / sec²(y)
Step 4: Express in terms of x
Recall the trigonometric identity: sec²(y) = 1 + tan²(y). Since tan(y) = 2x, we can substitute this into the equation:
dy/dx = 2 / (1 + tan²(y)) = 2 / (1 + (2x)²)
Step 5: Simplify
This simplifies to the same result as before:
dy/dx = 2 / (1 + 4x²)
Graphical Representation and Interpretation
The derivative, 2 / (1 + 4x²), tells us the instantaneous rate of change of arctan(2x) at any given point x. Graphically, it represents the slope of the tangent line to the curve y = arctan(2x) at that point. Notice that the denominator (1 + 4x²) is always positive, ensuring the derivative is always positive. This means the function arctan(2x) is always increasing. The derivative also approaches zero as x approaches positive or negative infinity, indicating that the rate of increase diminishes as x moves further from zero.
Applications and Relevance
The derivative of arctan(2x), and inverse trigonometric functions in general, plays a significant role in various areas of mathematics and its applications:
-
Calculus: It's fundamental to solving optimization problems, finding areas under curves, and analyzing the behavior of functions.
-
Physics: Inverse trigonometric functions frequently appear in models involving angles, trajectories, and oscillations. Derivatives are crucial for determining rates of change in these scenarios.
-
Engineering: Derivatives are essential for analyzing systems and predicting their behavior in various engineering disciplines, from electrical engineering to mechanical engineering.
-
Computer Graphics and Game Development: Inverse trigonometric functions and their derivatives are essential for calculations involving rotations, transformations, and vector operations.
Frequently Asked Questions (FAQ)
Q1: Why is the range of arctan(x) restricted?
A1: The tangent function is periodic, meaning it repeats its values every π radians. To define a proper inverse, we need to restrict the domain of the tangent function to an interval where it's one-to-one (meaning each input has a unique output). The interval (-π/2, π/2) is chosen for this purpose.
Q2: Can I use this method for other inverse trigonometric functions?
A2: Yes! The chain rule and implicit differentiation techniques demonstrated here can be applied to find derivatives of other inverse trigonometric functions such as arcsin(x), arccos(x), and arccot(x), with appropriate modifications based on their respective derivatives.
Q3: What if the inner function were more complex than 2x?
A3: The process remains the same. You would simply apply the chain rule, taking the derivative of the outer function (arctan(u)) and multiplying it by the derivative of the more complex inner function.
Q4: Are there any limitations to this derivative?
A4: The derivative is defined for all real numbers x. There are no points of discontinuity or non-differentiability.
Conclusion
Deriving the derivative of arctan(2x) might initially seem daunting, but by systematically applying the chain rule or implicit differentiation, the process becomes clear and manageable. Understanding the underlying principles and mastering these techniques is essential for success in calculus and related fields. This article provides not only the solution but also a thorough understanding of the concepts and their applications, empowering you to confidently tackle similar challenges in your mathematical endeavors. Remember that practice is key—try deriving the derivatives of other inverse trigonometric functions to solidify your understanding. The more you practice, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
103 Degrees F To C
Sep 08, 2025
-
Tattoo Of Eye Of Horus
Sep 08, 2025
-
1 Cubic Yard Cubic Meters
Sep 08, 2025
-
106 Degrees Fahrenheit To Celsius
Sep 08, 2025
-
Piano Chords In D Major
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of Inverse Tan 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.