Factor Of X 2 9
monicres
Sep 12, 2025 · 6 min read
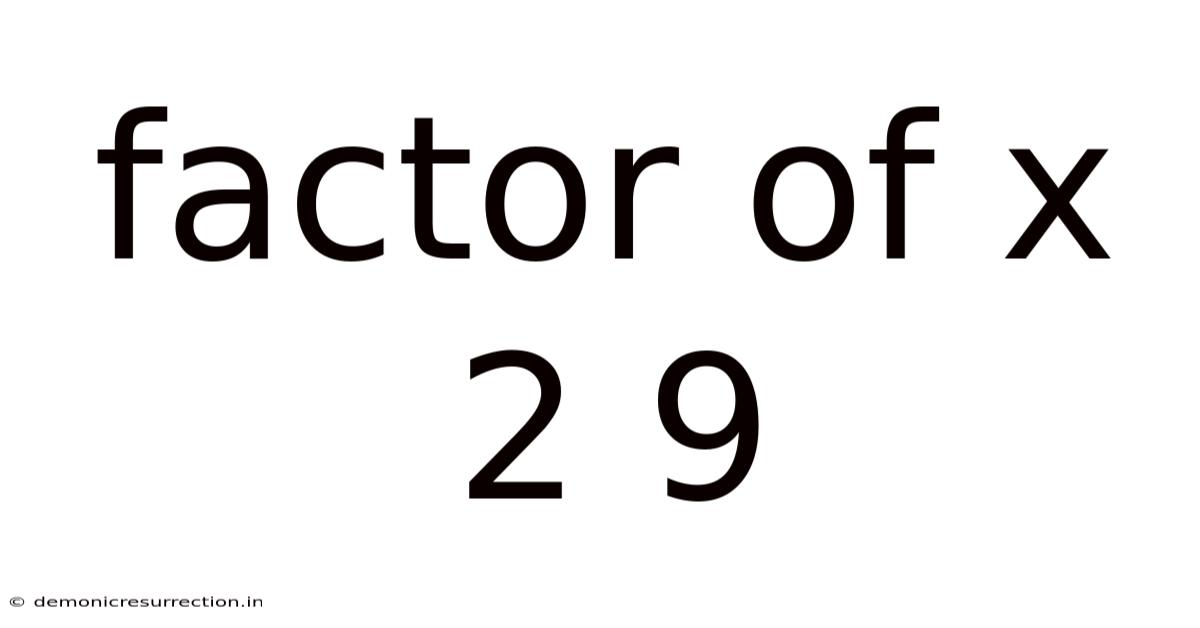
Table of Contents
Unraveling the Factors of x² - 9: A Deep Dive into Quadratic Expressions
Understanding the factors of a quadratic expression like x² - 9 is fundamental to success in algebra and beyond. This seemingly simple expression holds the key to understanding concepts like factoring, difference of squares, solving quadratic equations, and even more advanced mathematical principles. This comprehensive guide will delve into the factors of x² - 9, exploring not only the solution but also the underlying mathematical principles and applications. We'll break down the process step-by-step, making it accessible to learners of all levels.
Introduction: What are Factors?
Before we dive into the specific factors of x² - 9, let's define what we mean by "factors." In mathematics, factors are numbers or expressions that divide another number or expression without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly. Similarly, when we talk about factoring a quadratic expression, we're looking for expressions that, when multiplied together, result in the original quadratic.
Factoring x² - 9: The Difference of Squares
The expression x² - 9 is a special case known as a difference of squares. A difference of squares is any expression that can be written in the form a² - b², where 'a' and 'b' are any algebraic terms. The key characteristic is the subtraction sign separating two perfect squares.
In our case, x² - 9 can be rewritten as x² - 3², where 'a' is x and 'b' is 3. Both x² and 9 (which is 3²) are perfect squares. This specific form allows us to use a handy factorization formula:
a² - b² = (a + b)(a - b)
Applying this formula to x² - 9, we get:
x² - 9 = (x + 3)(x - 3)
Therefore, the factors of x² - 9 are (x + 3) and (x - 3). Multiplying these two factors back together using the FOIL method (First, Outer, Inner, Last) will confirm that we get the original expression:
(x + 3)(x - 3) = x² - 3x + 3x - 9 = x² - 9
Understanding the Concept: Why This Works
The reason this formula works is rooted in the concept of expanding binomials. Remember that (a + b)(a - b) means multiplying each term in the first binomial by each term in the second binomial. This results in:
a(a - b) + b(a - b) = a² - ab + ab - b² = a² - b²
The middle terms (-ab and +ab) cancel each other out, leaving only the difference of the squares. This cancellation is the essence of why the difference of squares factorization is so elegant and efficient.
Applications of Factoring x² - 9
The ability to factor x² - 9, and other quadratic expressions, has numerous applications in mathematics and beyond:
-
Solving Quadratic Equations: If we set x² - 9 equal to zero (x² - 9 = 0), we can use the factored form to find the roots (or solutions) of the equation. Since (x + 3)(x - 3) = 0, either (x + 3) = 0 or (x - 3) = 0. This gives us two solutions: x = -3 and x = 3. These are the x-intercepts of the parabola represented by the equation y = x² - 9.
-
Simplifying Algebraic Expressions: Factoring can simplify more complex algebraic expressions. For example, if you have an expression like (x² - 9) / (x + 3), you can simplify it by factoring the numerator: [(x + 3)(x - 3)] / (x + 3) = x - 3 (assuming x ≠ -3 to avoid division by zero).
-
Calculus: In calculus, factoring plays a crucial role in finding derivatives and integrals, simplifying complex functions, and solving optimization problems. The ability to quickly factor expressions like x² - 9 saves time and simplifies calculations.
-
Real-World Applications: Quadratic equations and their solutions are used to model various real-world phenomena, including projectile motion, the area of shapes, and many other scenarios in physics, engineering, and economics. Understanding how to factor these equations is essential for solving these practical problems.
Beyond x² - 9: Generalizing the Difference of Squares
The concept of the difference of squares extends far beyond the specific example of x² - 9. It applies to any expression in the form a² - b², where 'a' and 'b' can be numbers, variables, or more complex algebraic expressions. For instance:
-
4x² - 25: This can be factored as (2x + 5)(2x - 5) because 4x² = (2x)² and 25 = 5².
-
(x + 1)² - y²: This can be factored as [(x + 1) + y][(x + 1) - y] = (x + 1 + y)(x + 1 - y).
Understanding the general formula and its applications allows you to tackle a wider range of factoring problems efficiently.
Expanding Your Knowledge: Factoring Other Quadratic Expressions
While the difference of squares is a specific case, many other quadratic expressions can be factored using different techniques. Some common methods include:
-
Factoring Trinomials: Trinomials are quadratic expressions of the form ax² + bx + c. Factoring these involves finding two numbers that add up to 'b' and multiply to 'ac'.
-
Grouping: This method involves grouping terms with common factors to simplify the expression before factoring.
-
Completing the Square: This technique involves manipulating the expression to create a perfect square trinomial, which can then be factored easily.
Mastering these different techniques will equip you to factor a much wider range of quadratic expressions.
Frequently Asked Questions (FAQ)
Q1: What if the expression is x² + 9, not x² - 9?
A1: x² + 9 is a sum of squares, not a difference of squares. Sums of squares cannot be factored using real numbers. However, they can be factored using complex numbers, introducing the imaginary unit 'i' (where i² = -1). The factorization would be (x + 3i)(x - 3i).
Q2: Can I use the difference of squares method for expressions with higher powers, like x⁴ - 81?
A2: Yes! You can apply the difference of squares repeatedly. x⁴ - 81 can be written as (x²)² - 9², which factors to (x² + 9)(x² - 9). Then, you can further factor x² - 9 as (x + 3)(x - 3), resulting in the complete factorization: (x² + 9)(x + 3)(x - 3).
Q3: How can I check if my factoring is correct?
A3: Always multiply your factors back together using the distributive property or the FOIL method. If you get the original expression, your factoring is correct.
Q4: Are there any online tools or calculators that can help with factoring?
A4: While using tools can be helpful for checking answers, it's crucial to understand the underlying principles of factoring. The best way to master it is through practice and understanding the different techniques.
Conclusion: Mastering the Fundamentals
Understanding the factors of x² - 9 is more than just memorizing a formula; it's about grasping the fundamental concepts of factoring, the difference of squares, and their broader applications in algebra and beyond. By mastering this seemingly simple concept, you lay a solid foundation for tackling more complex mathematical problems and unlocking the doors to more advanced mathematical ideas. Remember to practice regularly and explore different techniques to build your proficiency and confidence. The journey of mastering algebra is one of continuous learning and exploration—enjoy the process!
Latest Posts
Latest Posts
-
Diagram Of Chloroplast With Labels
Sep 12, 2025
-
Lewis Dot Diagram Of Hcn
Sep 12, 2025
-
Lines Of Symmetry In Triangles
Sep 12, 2025
-
Famous Poems Of John Keats
Sep 12, 2025
-
Example Of Rule Of Law
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Factor Of X 2 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.