Half Of 1 1 2
monicres
Sep 09, 2025 · 5 min read
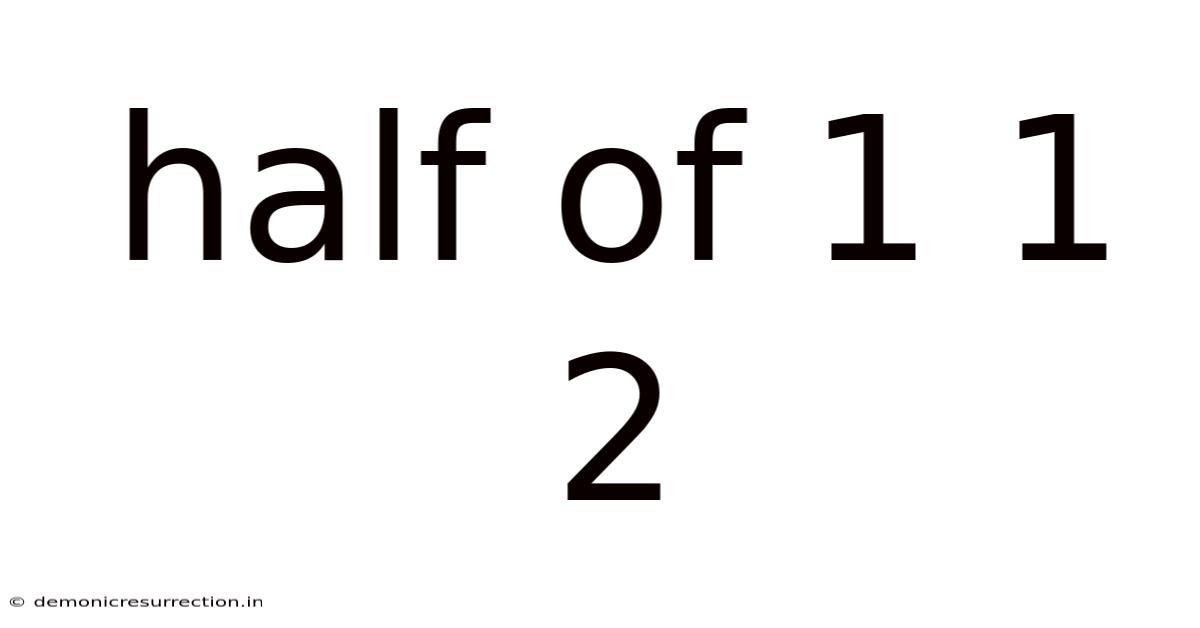
Table of Contents
Decoding "Half of 1 1 2": Exploring Fractions, Mixed Numbers, and Problem-Solving
What is half of 1 1 2? This seemingly simple question opens a door to a fascinating exploration of mathematical concepts like fractions, mixed numbers, and the crucial skill of problem-solving. Understanding how to solve this problem isn't just about finding the answer; it's about mastering fundamental mathematical principles that are applicable across various fields. This article will guide you through the process, offering detailed explanations and practical examples to solidify your understanding.
Understanding Fractions and Mixed Numbers
Before diving into the problem, let's refresh our understanding of fractions and mixed numbers. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator shows how many equal parts the whole is divided into. For example, 1/2 represents one out of two equal parts.
A mixed number combines a whole number and a fraction. For instance, 1 1/2 means one whole unit and one-half of another unit. It's crucial to be able to convert between improper fractions (where the numerator is larger than the denominator) and mixed numbers, as this is frequently necessary in calculations.
Breaking Down the Problem: "Half of 1 1 2"
The problem "half of 1 1 2" asks us to find half the value of the mixed number 1 1/2. To solve this, we need to follow a systematic approach:
Step 1: Convert the Mixed Number to an Improper Fraction
The first step is converting the mixed number 1 1/2 into an improper fraction. To do this, we multiply the whole number (1) by the denominator (2) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
1 1/2 = (1 * 2 + 1) / 2 = 3/2
Therefore, 1 1/2 is equivalent to the improper fraction 3/2.
Step 2: Find Half of the Improper Fraction
Now that we have an improper fraction, finding half is simply a matter of multiplication. We multiply the improper fraction (3/2) by 1/2 (which represents "half").
(3/2) * (1/2) = (3 * 1) / (2 * 2) = 3/4
Step 3: Interpreting the Result
The result, 3/4, means that half of 1 1/2 is equal to three-quarters. This fraction represents three out of four equal parts of a whole.
Visualizing the Solution
Visual aids can be incredibly helpful in understanding fractions. Imagine a circle divided into two equal halves. 1 1/2 would represent one whole circle plus half of another circle. If you divide this entire quantity into two equal parts, you'll see that each part represents three-quarters of a circle.
Alternative Approaches
While the method above is straightforward, let's explore alternative approaches to solving the same problem:
Approach 1: Finding Half of Each Part Separately
We can also tackle this problem by finding half of each component of the mixed number separately.
- Half of the whole number (1): 1/2 = 0.5
- Half of the fraction (1/2): (1/2) * (1/2) = 1/4 = 0.25
Adding these together, we get: 0.5 + 0.25 = 0.75, which is equivalent to 3/4.
Approach 2: Decimal Representation
We can convert the mixed number into a decimal and then find half of it.
- Convert 1 1/2 to decimal: 1 + (1/2) = 1 + 0.5 = 1.5
- Find half of 1.5: 1.5 / 2 = 0.75
Again, this confirms that half of 1 1/2 is 0.75, or 3/4.
The Importance of Understanding the Underlying Concepts
Solving "half of 1 1/2" is more than just performing calculations; it's about grasping the underlying concepts of fractions, mixed numbers, and the various methods for manipulating them. A solid understanding of these concepts is fundamental to success in more advanced mathematical topics like algebra, calculus, and beyond.
Furthermore, the ability to break down complex problems into smaller, manageable steps is a valuable skill transferable to many areas of life, not just mathematics. This problem-solving approach promotes critical thinking and enhances your analytical skills.
Frequently Asked Questions (FAQ)
- Q: Can I solve this problem using percentages?
A: Yes, you can! Since 1/2 is equivalent to 50%, the problem becomes "find 50% of 1 1/2". Converting 1 1/2 to a decimal (1.5) and multiplying by 0.5 (50%) gives you 0.75, which is still 3/4.
- Q: What if the problem involved a larger mixed number?
A: The same principles apply. You would first convert the mixed number to an improper fraction, then multiply by 1/2 (or divide by 2), and finally simplify the result if necessary.
- Q: Are there other ways to represent the answer (3/4)?
A: Yes! Besides the fraction 3/4 and the decimal 0.75, you could also represent it as a percentage (75%). The key is to understand that these are all different ways of expressing the same quantity.
- Q: Why is it important to understand both fractions and decimals?
A: Familiarity with both fractions and decimals is essential for flexibility in problem-solving. Some problems are easier to solve using fractions, while others are better tackled using decimals. Being comfortable with both representations allows you to choose the most efficient approach.
Conclusion: Mastering Fractions and Problem-Solving
Solving "half of 1 1 2" might seem trivial at first glance. However, this simple problem provides a valuable opportunity to reinforce fundamental mathematical concepts and problem-solving strategies. By mastering the conversion between mixed numbers and improper fractions and understanding various calculation methods, you build a stronger foundation for tackling more complex mathematical challenges in the future. The ability to break down problems, choose the appropriate approach, and confidently interpret results are skills that extend far beyond the realm of mathematics, proving invaluable in diverse academic and professional contexts. So, remember the journey is just as important as the destination – enjoy the process of learning and mastering these essential concepts!
Latest Posts
Latest Posts
-
Is 2 A Rational Number
Sep 09, 2025
-
Difference Between Religiosity And Spirituality
Sep 09, 2025
-
Life Of Pi Mirvish Review
Sep 09, 2025
-
3 X 5 X 2
Sep 09, 2025
-
Lewis Dot Structure For Cao
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.