Integral Of 1 3 X
monicres
Sep 16, 2025 · 6 min read
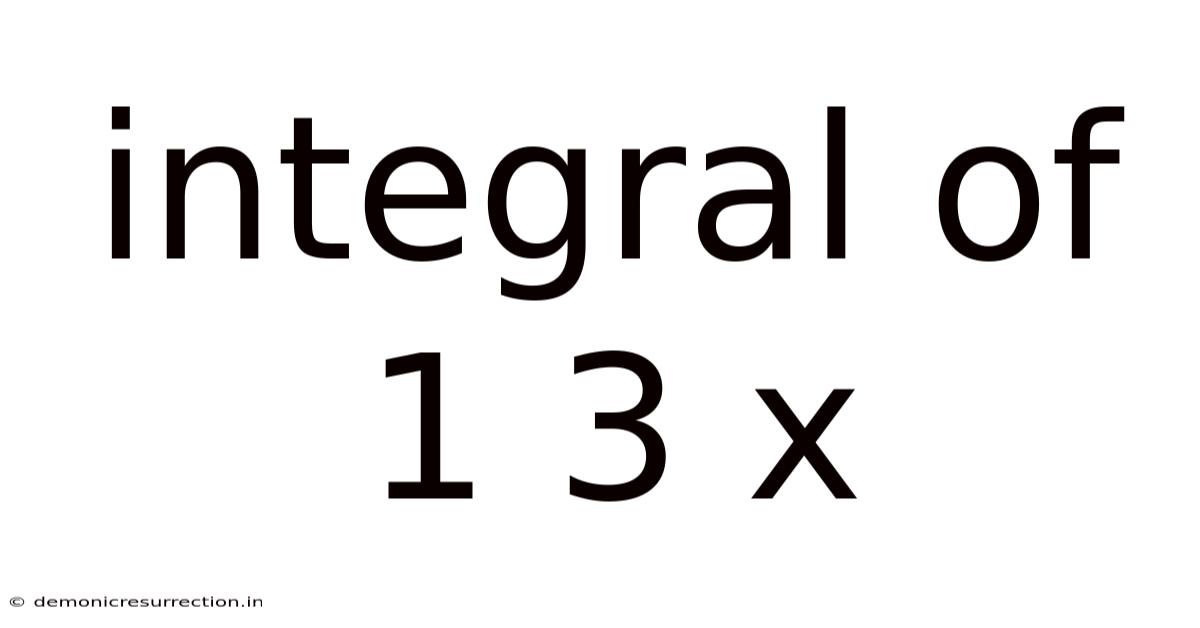
Table of Contents
Understanding and Solving the Integral of 1/(3x)
The integral of 1/(3x) is a fundamental concept in calculus, representing the antiderivative of the function 1/(3x). This seemingly simple integral introduces important concepts like logarithmic integration and the constant of integration. This article will provide a comprehensive explanation, covering the steps involved in solving the integral, its underlying mathematical principles, and frequently asked questions. Understanding this integral is crucial for mastering more advanced calculus concepts.
Introduction: What is an Integral?
Before delving into the specific integral, let's briefly recap the concept of integration. Integration is essentially the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the function whose derivative is the given function. This "original" function is called the antiderivative. The integral of a function f(x) is represented as ∫f(x)dx, where '∫' is the integral symbol, 'f(x)' is the integrand, and 'dx' indicates that the integration is with respect to the variable x.
The integral of 1/(3x) is a specific type of integral known as an indefinite integral, because it doesn't have defined limits of integration. Indefinite integrals always include a constant of integration (+C) to account for the fact that many functions can have the same derivative.
Step-by-Step Solution: Integrating 1/(3x)
Let's break down the process of solving the integral of 1/(3x):
-
Constant Factor: The first step is to recognize that 1/(3x) can be rewritten as (1/3) * (1/x). The constant factor (1/3) can be pulled outside the integral sign, simplifying the calculation. This is based on the linearity property of integrals: ∫cf(x)dx = c∫f(x)dx, where 'c' is a constant.
-
Integral of 1/x: The core of this problem lies in integrating 1/x. This is a standard integral that results in the natural logarithm function. Specifically, ∫(1/x)dx = ln|x| + C. The absolute value is crucial here because the natural logarithm is only defined for positive arguments. Including the absolute value ensures the result is valid for both positive and negative values of x.
-
Combining the Steps: Combining the steps above, we have:
∫(1/(3x))dx = (1/3) ∫(1/x)dx = (1/3)ln|x| + C
Therefore, the integral of 1/(3x) is (1/3)ln|x| + C, where C is the constant of integration.
Mathematical Explanation: Why ln|x|?
The result ln|x| stems from the fundamental theorem of calculus and the properties of the exponential and logarithmic functions. The derivative of e<sup>x</sup> is e<sup>x</sup> itself. Consider the function y = e<sup>x</sup>. If we differentiate this, we get dy/dx = e<sup>x</sup>. Now, let's think about the inverse function of e<sup>x</sup>, which is ln(x). By the inverse function theorem, the derivative of ln(x) is 1/x for x > 0. This is why the integral of 1/x is ln(x) for positive x. To extend this to negative x, we use the absolute value, resulting in ln|x|.
This relationship between the exponential and natural logarithm functions is fundamental to understanding why the integral of 1/x results in a logarithmic function. It's a direct consequence of the inverse relationship and the properties of differentiation and integration.
Definite Integral of 1/(3x)
While the previous sections dealt with the indefinite integral, let's also consider the definite integral, which involves limits of integration. The definite integral of 1/(3x) from a to b is written as:
∫<sub>a</sub><sup>b</sup> (1/(3x)) dx
To solve this, we first find the indefinite integral, as shown above: (1/3)ln|x| + C. Then, we evaluate this expression at the upper limit (b) and subtract the value at the lower limit (a):
[(1/3)ln|b| + C] - [(1/3)ln|a| + C]
Notice that the constant of integration (C) cancels out, which is always the case with definite integrals. The final result is:
(1/3)(ln|b| - ln|a|) = (1/3)ln|b/a|
Applications of the Integral of 1/(3x)
The integral of 1/(3x) and related logarithmic integrals have numerous applications in various fields, including:
- Physics: Solving differential equations related to exponential decay or growth processes, such as radioactive decay or population dynamics.
- Engineering: Analyzing circuits involving capacitors and resistors, calculating fluid flow, or modeling heat transfer.
- Economics: Modeling economic growth, calculating present value of future income streams, and analyzing investment strategies.
- Probability and Statistics: Dealing with probability density functions involving exponential distributions.
Common Mistakes to Avoid
Here are some common errors students make when dealing with this integral:
- Forgetting the absolute value: Always remember to include the absolute value |x| within the natural logarithm. This ensures the function is defined for both positive and negative values of x.
- Ignoring the constant of integration (C): This is crucial for indefinite integrals. Omitting C is a significant mathematical error.
- Incorrectly handling the constant factor: Ensure you correctly pull out the constant (1/3) before integrating.
Frequently Asked Questions (FAQ)
-
Q: What happens if x = 0?
A: The function 1/(3x) is undefined at x = 0. The integral itself is improper at x = 0 and requires special handling using limits.
-
Q: Can I simplify (1/3)ln|x| further?
A: No, there's no further simplification possible unless you have specific values for x.
-
Q: What if the integral were ∫(1/(3x+2))dx?
A: This requires a u-substitution. Let u = 3x+2, then du = 3dx. The integral becomes (1/3)∫(1/u)du = (1/3)ln|u| + C = (1/3)ln|3x+2| + C.
-
Q: What about the integral of 1/(ax+b), where a and b are constants?
A: Similar to the previous question, a u-substitution is needed. Let u = ax+b, then du = adx. The integral becomes (1/a)∫(1/u)du = (1/a)ln|u| + C = (1/a)ln|ax+b| + C.
-
Q: Why is the constant of integration important?
A: The constant of integration represents the family of functions that share the same derivative. Without it, the solution is incomplete and only represents one specific member of this family.
Conclusion: Mastering the Integral of 1/(3x)
The integral of 1/(3x), while appearing simple at first glance, embodies key concepts in integral calculus. Understanding the step-by-step solution, the underlying mathematical principles linking logarithms and exponentials, and the common pitfalls allows for a solid grasp of this fundamental integral. This foundational knowledge will prove invaluable as you progress to more complex integration techniques and applications within mathematics, science, and engineering. Remember to practice consistently, paying attention to detail, especially regarding the absolute value and the constant of integration. Mastering this simple integral lays a crucial groundwork for a deeper understanding of calculus as a whole.
Latest Posts
Latest Posts
-
Map Of New France 1713
Sep 16, 2025
-
How Big Is 60 Inches
Sep 16, 2025
-
Berenstain Bears Green Eyed Monster
Sep 16, 2025
-
Peace Goddess Crossword Puzzle Clue
Sep 16, 2025
-
36 Is How Many Feet
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 3 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.