Integral Of 1 X 2
monicres
Sep 11, 2025 · 5 min read
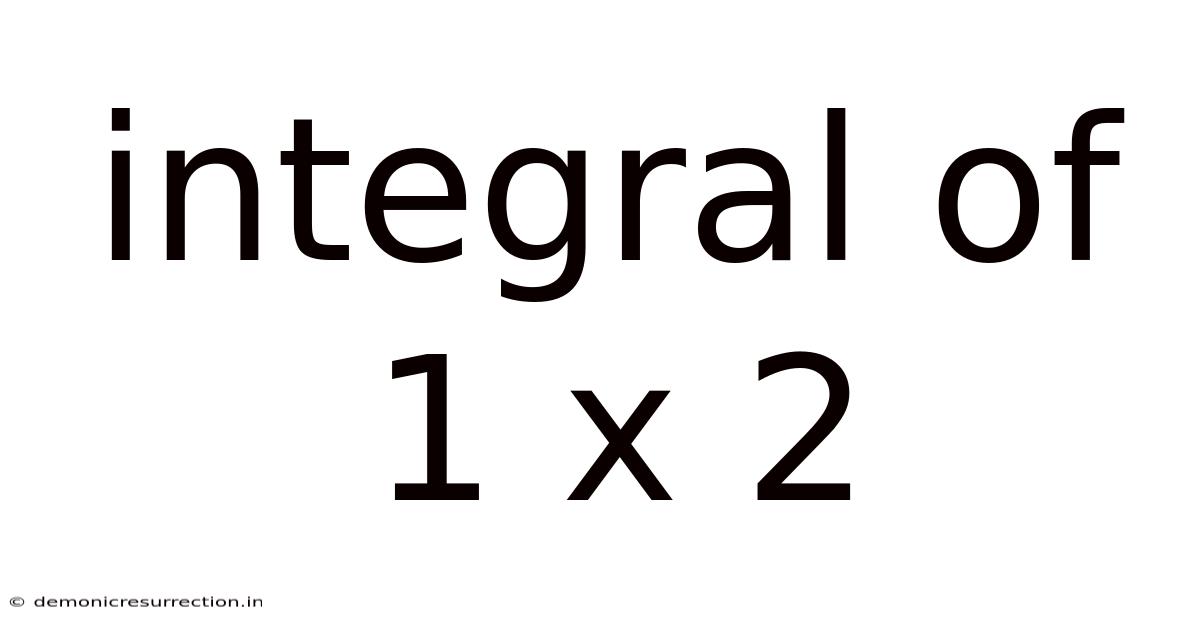
Table of Contents
Understanding and Solving the Integral of 1/x²: A Comprehensive Guide
The integral of 1/x², often written as ∫(1/x²)dx, is a fundamental concept in calculus. This seemingly simple integral unlocks doors to understanding various applications in physics, engineering, and other scientific fields. This comprehensive guide will walk you through the process of solving this integral, explaining the underlying principles and providing a deeper understanding of its implications. We will cover the mathematical process, explore its applications, and address frequently asked questions. Understanding this integral is crucial for mastering more advanced calculus concepts.
Introduction: A Gentle Start with Power Rule
Before diving into the specifics of integrating 1/x², let's refresh our understanding of the power rule of integration. The power rule states that the integral of xⁿ dx is (xⁿ⁺¹)/(n+1) + C, where 'n' is any real number except -1, and 'C' is the constant of integration. This constant is crucial because the derivative of a constant is always zero; therefore, any constant can be added to the result of integration without affecting its validity.
Now, let's rewrite our problem: ∫(1/x²)dx can be rewritten as ∫x⁻²dx. This form aligns perfectly with the power rule.
Step-by-Step Solution: Applying the Power Rule
-
Rewrite the integrand: As mentioned above, we rewrite 1/x² as x⁻². This simple algebraic manipulation is the key to unlocking the solution.
-
Apply the power rule: Now, we apply the power rule directly. Following the formula, we have:
∫x⁻²dx = (x⁻²⁺¹)/(-2+1) + C
-
Simplify the expression: Simplifying the exponent and the denominator, we get:
(x⁻¹)/(-1) + C = -x⁻¹ + C
-
Express the result in a more conventional form: Finally, we can express the result without negative exponents:
-1/x + C
Therefore, the integral of 1/x² is -1/x + C.
Understanding the Constant of Integration (C)
The constant of integration, 'C', is a critical component of the indefinite integral. It represents the family of functions whose derivatives are all equal to 1/x². To visualize this, imagine plotting several functions of the form -1/x + C, where C takes different values (e.g., 0, 1, -2, etc.). Each function will have the same slope at any given x-value, but they will be vertically shifted relative to each other. The constant 'C' accounts for this vertical shift.
If we had a definite integral (with specified limits of integration), the constant of integration would cancel out during the evaluation process. However, with indefinite integrals, it is essential to include the constant 'C' to represent the complete solution.
A Deeper Dive: The Antiderivative Perspective
Integration is essentially the reverse process of differentiation. The antiderivative of a function f(x) is a function F(x) such that F'(x) = f(x). In our case, f(x) = 1/x², and we found its antiderivative to be F(x) = -1/x + C. To verify this, we can differentiate F(x) using the power rule for differentiation:
d/dx (-1/x + C) = d/dx (-x⁻¹ + C) = -(-1)x⁻² = x⁻² = 1/x²
This confirms that our integrated solution is correct.
Applications in Real-World Scenarios
The integral of 1/x² finds applications in various areas:
-
Physics: Calculating the work done by a variable force, determining the potential energy associated with a specific force field, and solving problems related to gravitational or electrostatic forces often involve integrating functions similar to 1/x².
-
Engineering: In structural engineering, calculating stress distributions and analyzing bending moments might require solving integrals involving inverse square functions. Similarly, it appears in fluid dynamics and heat transfer problems.
-
Economics: Certain economic models use functions inversely proportional to the square of a variable, requiring the integral of 1/x² for calculations related to marginal cost, utility functions, or demand elasticity.
-
Probability and Statistics: Although less directly, the integral of functions related to 1/x² can appear in the context of probability density functions or related concepts in statistical analysis.
Common Mistakes and How to Avoid Them
-
Forgetting the constant of integration (C): Always remember to include '+ C' in the solution of an indefinite integral. This is a common error that can lead to an incomplete or incorrect answer.
-
Incorrect application of the power rule: Ensure you correctly add 1 to the exponent and divide by the new exponent. A slight mistake in the arithmetic can lead to significant errors in the final result.
-
Not rewriting the integrand appropriately: Remember to rewrite 1/x² as x⁻² before applying the power rule.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a definite and an indefinite integral?
A1: An indefinite integral gives a general solution, including the constant of integration (C). A definite integral, on the other hand, gives a numerical value calculated between specified limits of integration. The constant of integration cancels out in definite integrals.
Q2: Can we integrate 1/x² if the exponent were different, say, 1/x³ or 1/xⁿ?
A2: Yes, absolutely! The power rule can be applied to any power of x except for x⁻¹. For example, ∫x⁻³dx = (x⁻²)/(-2) + C = -1/(2x²) + C. The case of ∫1/x dx = ∫x⁻¹dx requires a different approach, leading to the natural logarithm function (ln|x| + C).
Q3: What happens if we try to integrate 1/x² from 0 to 1?
A3: The integral ∫(from 0 to 1) (1/x²)dx is an improper integral because the function 1/x² is undefined at x=0. The limit as the lower bound approaches 0 results in an infinite value, indicating the integral diverges.
Q4: Are there other methods to solve this integral besides the power rule?
A4: For this particular integral, the power rule is the most straightforward and efficient method. More complex integrals might require techniques such as integration by parts, u-substitution, or partial fraction decomposition, but these are not necessary for ∫(1/x²)dx.
Conclusion: Mastering a Fundamental Concept
The integral of 1/x², while seemingly simple, represents a fundamental concept in calculus with significant applications across diverse scientific and engineering fields. By understanding the step-by-step process, the significance of the constant of integration, and the potential pitfalls, you can confidently tackle this integral and build a strong foundation for more advanced calculus concepts. Remember to practice regularly and always verify your solution by differentiating the result. Through consistent effort, you can master this crucial element of integral calculus.
Latest Posts
Latest Posts
-
Yellow And Green And Blue
Sep 11, 2025
-
Product Rule And Quotient Rule
Sep 11, 2025
-
What Is 20 Of 500
Sep 11, 2025
-
Nancy Thayer Books In Order
Sep 11, 2025
-
Kinetic Energy Of A Spring
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.