Is 1/3 More Than 1/2
monicres
Sep 18, 2025 · 6 min read
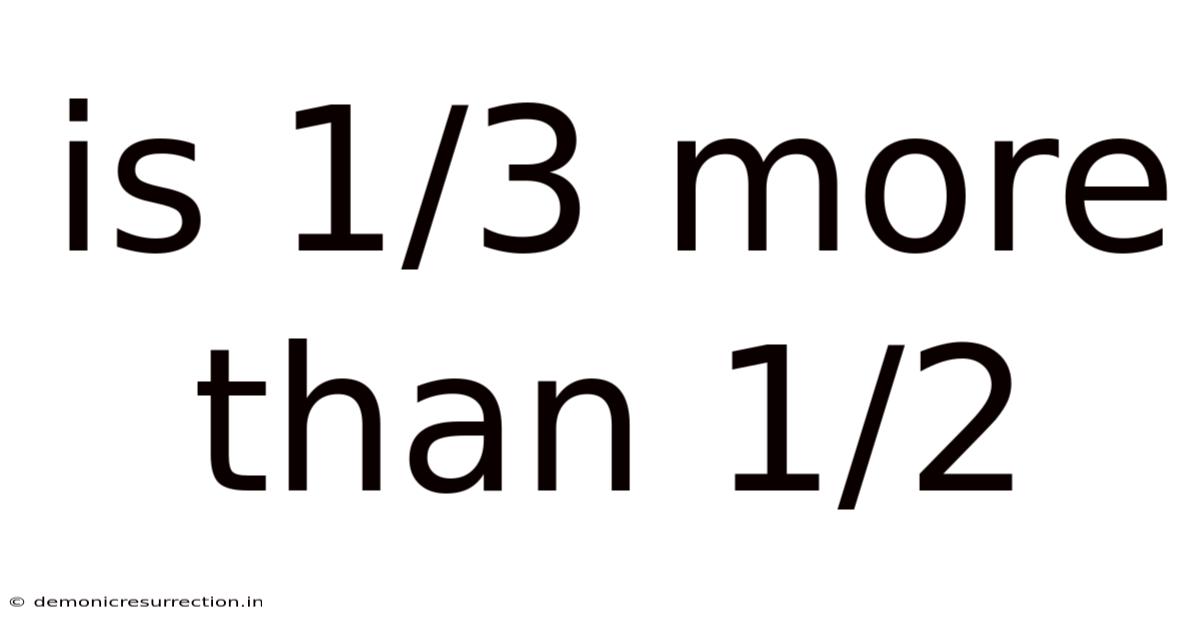
Table of Contents
Is 1/3 More Than 1/2? Understanding Fractions and Comparisons
Is 1/3 more than 1/2? This seemingly simple question touches upon fundamental concepts in mathematics, particularly the understanding and comparison of fractions. The answer, of course, is no, but understanding why requires a deeper dive into fractional representation, visual aids, and practical applications. This article will explore these aspects, equipping you with a comprehensive understanding of fractions and how to compare their values effectively.
Introduction to Fractions
A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 1/2, the denominator (2) means the whole is divided into two equal parts, and the numerator (1) indicates we are considering one of those parts.
Visualizing Fractions: A Pictorial Approach
Visual aids are incredibly helpful in understanding fractions, especially when comparing them. Let's visualize 1/2 and 1/3:
Imagine a single pizza.
-
1/2: If you cut the pizza into two equal slices, 1/2 represents one of those slices. It's a relatively large portion.
-
1/3: If you cut the same pizza into three equal slices, 1/3 represents only one of those three slices. This slice is noticeably smaller than the 1/2 slice.
This visual representation clearly shows that 1/2 is larger than 1/3. The larger the denominator, the smaller the individual parts of the whole become.
Comparing Fractions: Methods and Techniques
There are several ways to compare fractions:
-
Visual Comparison (as shown above): This is excellent for introductory understanding. Drawing diagrams or using physical objects helps build an intuitive grasp of fractional values.
-
Common Denominator Method: This is the most common and reliable method for comparing fractions. To compare 1/2 and 1/3, we find a common denominator (a number that is divisible by both 2 and 3). The least common multiple of 2 and 3 is 6. We then convert both fractions to have a denominator of 6:
- 1/2 = (1 x 3) / (2 x 3) = 3/6
- 1/3 = (1 x 2) / (3 x 2) = 2/6
Now it's clear that 3/6 (1/2) is greater than 2/6 (1/3).
-
Decimal Conversion: Convert both fractions into decimals. 1/2 = 0.5 and 1/3 = 0.333... (a repeating decimal). Again, it's evident that 0.5 is larger than 0.333...
-
Cross-Multiplication: This method is particularly useful when comparing fractions with different numerators and denominators. To compare a/b and c/d, you cross-multiply: a x d and b x c.
- If a x d > b x c, then a/b > c/d
- If a x d < b x c, then a/b < c/d
- If a x d = b x c, then a/b = c/d
Let's apply this to 1/2 and 1/3:
- 1 x 3 = 3
- 2 x 1 = 2
- Since 3 > 2, 1/2 > 1/3
Understanding the Relationship Between Numerator and Denominator
The relative sizes of the numerator and denominator significantly impact the value of the fraction.
-
Numerator and Denominator are Equal: If the numerator and denominator are equal (e.g., 2/2, 5/5, etc.), the fraction equals 1, representing the whole.
-
Numerator Smaller Than Denominator: If the numerator is smaller than the denominator (e.g., 1/2, 3/4, etc.), the fraction represents a part of the whole, less than 1 (a proper fraction).
-
Numerator Larger Than Denominator: If the numerator is larger than the denominator (e.g., 5/2, 7/3, etc.), the fraction represents more than one whole (an improper fraction). These can be expressed as mixed numbers (e.g., 5/2 = 2 1/2).
Real-World Applications: Where Do We Use Fractions?
Fractions are ubiquitous in everyday life:
-
Cooking and Baking: Recipes often involve fractional measurements (e.g., 1/2 cup of flour, 1/4 teaspoon of salt).
-
Measurement: We use fractions to measure lengths, weights, and volumes (e.g., 1/8 inch, 1/2 kilogram).
-
Time: We express time in fractions (e.g., 1/2 hour, 1/4 of a day).
-
Money: Money uses fractions (e.g., 1/4 of a dollar is 25 cents).
-
Probability and Statistics: Fractions are used to represent probabilities and proportions.
-
Geometry and Trigonometry: Fractions are fundamental in geometrical calculations.
Addressing Common Misconceptions
A common misconception is that a larger numerator automatically means a larger fraction. This is only true if the denominators are the same. Comparing 1/2 and 2/5 requires finding a common denominator or using another comparison method.
Another misconception involves incorrectly adding or subtracting fractions without a common denominator. You cannot directly add 1/2 and 1/3 by simply adding the numerators and denominators (1+1)/(2+3) = 2/5. This is incorrect. You must first find a common denominator before performing addition or subtraction.
Frequently Asked Questions (FAQ)
-
Q: How can I easily compare fractions with different denominators?
- A: The most reliable method is to find a common denominator and convert both fractions to equivalent fractions with that common denominator. Alternatively, you can convert the fractions to decimals or use cross-multiplication.
-
Q: What is a mixed number?
- A: A mixed number is a combination of a whole number and a proper fraction (e.g., 2 1/3).
-
Q: How do I convert an improper fraction to a mixed number?
- A: Divide the numerator by the denominator. The quotient is the whole number part of the mixed number, and the remainder is the numerator of the fractional part, with the denominator remaining the same. For example, 7/3 = 2 with a remainder of 1, so 7/3 = 2 1/3.
-
Q: Are there any online tools that can help me compare fractions?
- A: Yes, many online calculators and educational websites offer fraction comparison tools. These can be very helpful for checking your work or practicing fraction comparison skills.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Understanding fractions is crucial for building a solid foundation in mathematics. The ability to compare and manipulate fractions is essential in various fields, from everyday tasks to advanced scientific calculations. While the answer to the initial question – Is 1/3 more than 1/2? – is a simple "no," the journey to understanding why has opened up a wealth of knowledge about fractional representation, comparison techniques, and their practical applications. By mastering these fundamental concepts, you'll develop a stronger mathematical understanding and equip yourself with essential tools for success in many aspects of life. Remember to utilize visual aids, practice different comparison methods, and don't hesitate to explore online resources to solidify your understanding of fractions.
Latest Posts
Latest Posts
-
Shoot For The Stars Quote
Sep 18, 2025
-
Awards Won By Mother Teresa
Sep 18, 2025
-
How Long Is Confederation Bridge
Sep 18, 2025
-
Examples Of Sole Proprietorship Companies
Sep 18, 2025
-
I Am A Serial Killer
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 1/3 More Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.