Is 3/4 Bigger Than 2/3
monicres
Sep 16, 2025 · 6 min read
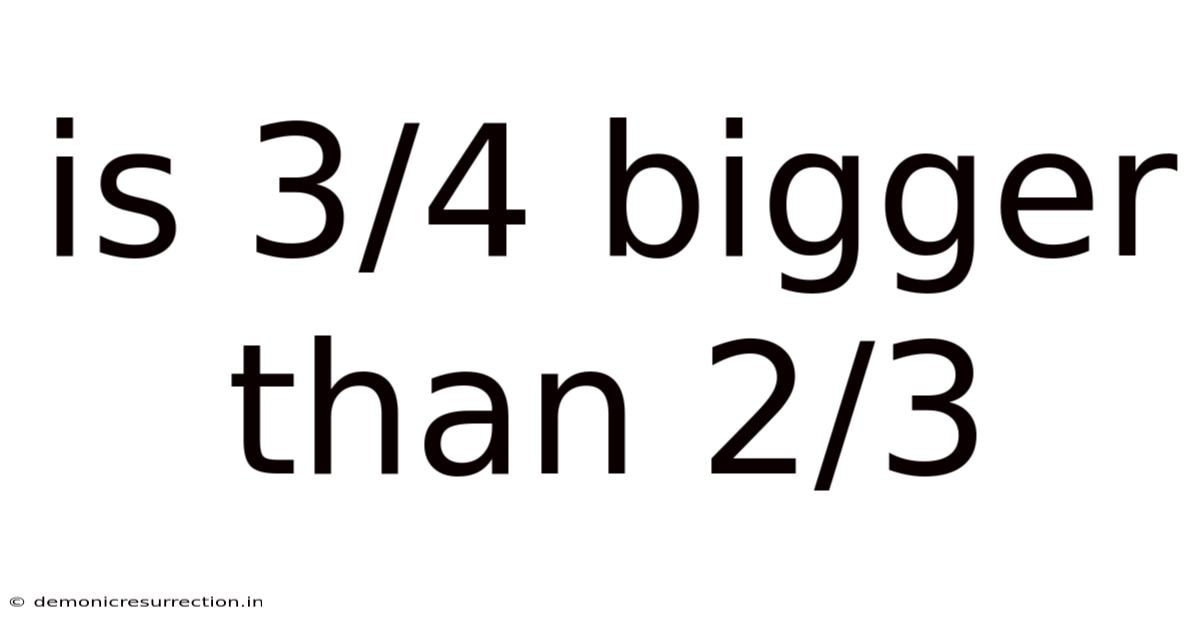
Table of Contents
Is 3/4 Bigger Than 2/3? A Deep Dive into Fraction Comparison
This article will explore the question: "Is 3/4 bigger than 2/3?" We'll not only answer this specific question but delve into the broader topic of comparing fractions, providing you with the tools and understanding to tackle similar comparisons confidently. Understanding fraction comparison is a fundamental skill in mathematics, crucial for various applications from baking to advanced calculus. We'll cover different methods, explain the underlying principles, and even touch upon the practical applications of this knowledge.
Introduction: Understanding Fractions
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For instance, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4 equal parts.
Method 1: Finding a Common Denominator
The most straightforward way to compare fractions is by finding a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's apply this to our problem: Is 3/4 bigger than 2/3?
-
Step 1: Find the least common multiple (LCM) of the denominators (4 and 3). The LCM of 4 and 3 is 12. This is the smallest number that both 4 and 3 can divide into evenly.
-
Step 2: Convert both fractions to equivalent fractions with the common denominator (12).
-
To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
-
Step 3: Compare the numerators. Now we have 9/12 and 8/12. Since 9 > 8, we can conclude that 9/12 is bigger than 8/12.
-
Step 4: State the conclusion. Therefore, 3/4 is bigger than 2/3.
Method 2: Converting to Decimals
Another approach is to convert both fractions to decimals and then compare them. This method is particularly useful when dealing with more complex fractions or when you're more comfortable working with decimals.
-
Step 1: Convert 3/4 to a decimal. Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Step 2: Convert 2/3 to a decimal. Divide the numerator (2) by the denominator (3): 2 ÷ 3 = 0.666... (a repeating decimal)
-
Step 3: Compare the decimals. Since 0.75 > 0.666..., we can conclude that 3/4 is bigger than 2/3.
Method 3: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. You can represent fractions using diagrams like circles or rectangles.
Imagine two identical circles.
-
Divide the first circle into four equal parts and shade three of them. This represents 3/4.
-
Divide the second circle into three equal parts and shade two of them. This represents 2/3.
By visually comparing the shaded areas, it becomes clear that the shaded area in the first circle (3/4) is larger than the shaded area in the second circle (2/3). This visual comparison reinforces the conclusion that 3/4 is bigger than 2/3.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is crucial in many aspects of life, both academic and practical. Here are a few examples:
-
Cooking and Baking: Recipes often require precise measurements using fractions. Understanding fraction comparison allows you to accurately adjust recipes or determine which ingredient requires a larger quantity.
-
Construction and Engineering: Precision is paramount in construction and engineering projects. Calculations often involve fractions, and the ability to compare them is essential for ensuring accuracy and safety.
-
Data Analysis: Many data sets involve fractions or proportions. Understanding fraction comparison is vital for interpreting and analyzing data effectively.
-
Finance: Calculations involving interest rates, discounts, and profit margins often involve fractions. The ability to compare fractions is crucial for making sound financial decisions.
Beyond the Basics: Comparing More Complex Fractions
The methods discussed above work well for simple fractions. However, when comparing more complex fractions, understanding the relative size of the fractions becomes more important. Consider these points:
-
Fractions close to 1: A fraction is closer to 1 if the numerator is close to the denominator. For example, 7/8 is closer to 1 than 2/3.
-
Fractions close to 0: A fraction is closer to 0 if the numerator is significantly smaller than the denominator. For example, 1/10 is closer to 0 than 3/4.
-
Improper Fractions: Improper fractions (where the numerator is greater than or equal to the denominator) are always greater than or equal to 1. They can be converted to mixed numbers (a whole number and a fraction) for easier comparison.
Frequently Asked Questions (FAQ)
Q1: What if the denominators are very large? Does the common denominator method become cumbersome?
A1: Yes, finding the LCM of very large denominators can be time-consuming. In such cases, converting to decimals or using a calculator to perform the division might be a more efficient approach.
Q2: Are there any shortcuts for comparing fractions without using the common denominator method?
A2: While finding a common denominator is generally the most reliable method, you can sometimes make quick comparisons if the fractions are relatively simple. For example, if you have fractions with the same numerator, the fraction with the smaller denominator will be larger (e.g., 2/3 > 2/5).
Q3: How can I explain fraction comparison to a young child?
A3: Use visual aids like pizza slices or chocolate bars. Divide the visual aid into equal parts and shade the relevant fraction. Comparing the shaded areas makes the comparison clear and easy to understand.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill with wide-ranging applications. By understanding the different methods – finding a common denominator, converting to decimals, and using visual representations – you can confidently tackle fraction comparisons in various contexts. Remember to choose the method most comfortable and efficient for the specific problem at hand. The more you practice, the more intuitive this skill will become, making it easier to handle more complex mathematical problems in the future. From baking a perfect cake to solving complex engineering challenges, a solid understanding of fraction comparison is a valuable asset. So, the next time you encounter a fraction comparison problem, remember the techniques we've explored here, and you'll be well-equipped to find the solution with confidence.
Latest Posts
Latest Posts
-
How To Work A Sextant
Sep 16, 2025
-
Saint Mary Margaret Catholic Church
Sep 16, 2025
-
1 Tablespoon Cinnamon In Grams
Sep 16, 2025
-
How Far Is Five Miles
Sep 16, 2025
-
Molecular Mass Of 1 Butanol
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Bigger Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.