Is 5/16th Bigger Than 1/4
monicres
Sep 21, 2025 · 5 min read
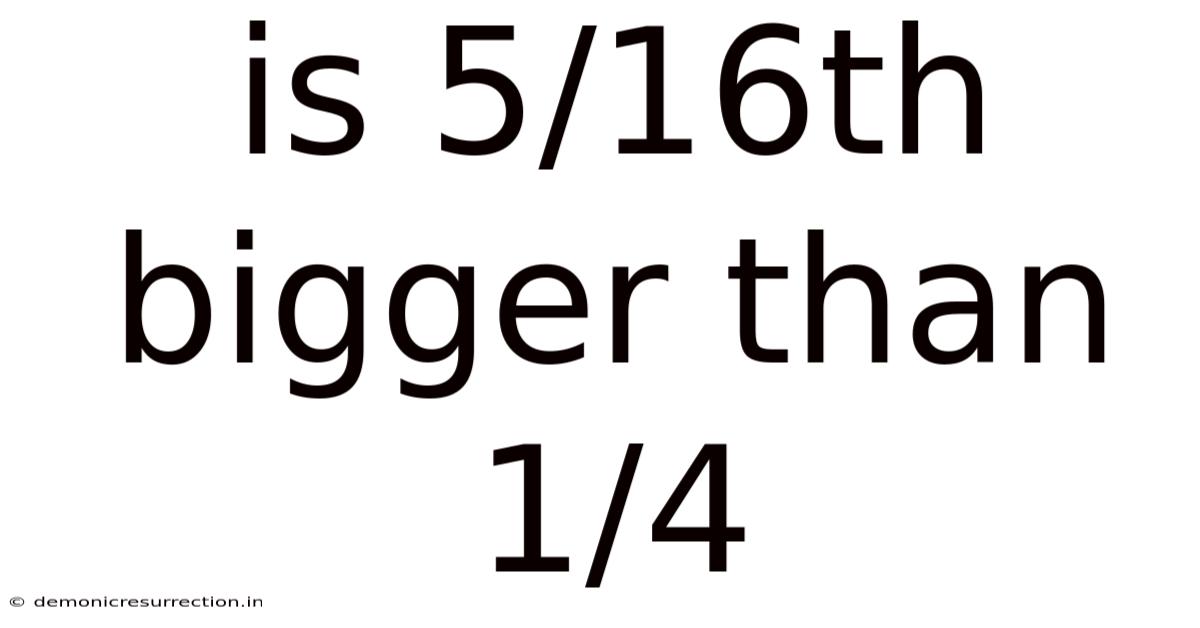
Table of Contents
Is 5/16th Bigger Than 1/4? A Deep Dive into Fraction Comparison
Are you struggling with comparing fractions? It's a common hurdle in mathematics, but mastering it unlocks a deeper understanding of numbers and their relationships. This article will comprehensively address the question: Is 5/16th bigger than 1/4? We'll not only answer this specific question but also explore various methods for comparing fractions, providing you with the tools to confidently tackle similar problems in the future. Understanding fraction comparison is fundamental for success in algebra, calculus, and numerous real-world applications.
Understanding Fractions: A Quick Refresher
Before we dive into the comparison, let's review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 out of 4 equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's apply this method to compare 5/16 and 1/4.
-
Find the least common multiple (LCM) of the denominators: The denominators are 16 and 4. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 16 are 16, 32, 48... The least common multiple is 16.
-
Convert the fractions to equivalent fractions with the common denominator:
- 5/16 already has a denominator of 16, so it remains unchanged.
- To convert 1/4 to a fraction with a denominator of 16, we multiply both the numerator and the denominator by 4: (1 x 4) / (4 x 4) = 4/16
-
Compare the numerators: Now we compare 5/16 and 4/16. Since 5 > 4, we can conclude that 5/16 > 4/16.
Therefore, 5/16 is bigger than 1/4.
Method 2: Converting to Decimals
Another effective method is to convert both fractions to decimals. This involves dividing the numerator by the denominator.
-
Convert 5/16 to a decimal: 5 ÷ 16 = 0.3125
-
Convert 1/4 to a decimal: 1 ÷ 4 = 0.25
Comparing the decimal values, we see that 0.3125 > 0.25. Therefore, 5/16 is bigger than 1/4.
Method 3: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. Imagine a pizza cut into 16 slices (representing 16ths) and another pizza cut into 4 slices (representing quarters).
- If you take 5 slices from the pizza cut into 16, you have a larger portion than if you take 1 slice from the pizza cut into 4.
This visual representation confirms that 5/16 is bigger than 1/4.
Method 4: Using Cross-Multiplication
Cross-multiplication is a quick method for comparing fractions. We multiply the numerator of the first fraction by the denominator of the second fraction and vice versa. The larger product corresponds to the larger fraction.
-
Cross-multiply: (5 x 4) = 20 and (16 x 1) = 16
-
Compare the products: Since 20 > 16, we can conclude that 5/16 > 1/4.
This method provides a concise and efficient way to compare fractions, especially when dealing with larger numbers.
Understanding the Difference: A Deeper Look
The difference between 5/16 and 1/4 might seem small, but understanding the underlying concepts reinforces the importance of precise calculations. The difference is 5/16 - 4/16 = 1/16. While seemingly insignificant in isolation, such differences can accumulate and become significant in various contexts, such as engineering, finance, and scientific measurements. Accuracy in fraction comparison is paramount for reliable results.
Real-World Applications of Fraction Comparison
The ability to compare fractions is not just an academic exercise. It has practical applications in numerous areas:
-
Cooking and Baking: Following recipes often requires precise measurements, where understanding fractions is essential for achieving the desired results.
-
Construction and Engineering: Accurate measurements are critical in construction and engineering projects. Fraction comparison ensures the correct dimensions and proportions are maintained.
-
Finance and Budgeting: Calculating proportions of income, expenses, and investments often involves working with fractions and percentages, which are directly related to fractions.
-
Data Analysis: Many statistical calculations involve analyzing data expressed as fractions or proportions.
-
Computer Programming: Many programming tasks require precise calculations and comparisons, including those involving fractional values.
Frequently Asked Questions (FAQ)
Q: Can I always use the common denominator method?
A: Yes, the common denominator method is a reliable method that works for all fraction comparisons. However, other methods, like decimal conversion or cross-multiplication, can be faster in some cases.
Q: What if the fractions have different signs (one positive and one negative)?
A: A positive fraction is always greater than a negative fraction.
Q: Are there any online tools or calculators to help with fraction comparison?
A: Yes, many online calculators and tools can help you compare fractions quickly and easily. These tools can be particularly helpful when dealing with complex fractions. However, understanding the underlying principles is crucial for true mastery.
Q: Is there a shortcut for comparing fractions with the same numerator but different denominators?
A: Yes, if the numerators are the same, the fraction with the smaller denominator is the larger fraction. For example, 3/4 is larger than 3/8.
Q: What is the best method for comparing fractions?
A: There isn't one single "best" method. The optimal approach depends on the specific fractions involved and your personal preference. Understanding multiple methods provides flexibility and allows you to choose the most efficient approach for each situation.
Conclusion
Comparing fractions is a fundamental mathematical skill with broad applications across various fields. This article has provided a comprehensive exploration of various methods for comparing fractions, including finding a common denominator, converting to decimals, visual representation, and cross-multiplication. By mastering these techniques, you'll not only be able to confidently answer the question, "Is 5/16 bigger than 1/4?" but also tackle any fraction comparison problem with ease and accuracy. Remember, practice is key to mastering this essential mathematical concept. The more you practice, the more intuitive and effortless fraction comparison will become. The seemingly simple question of comparing 5/16 and 1/4 opens up a world of understanding regarding numerical relationships and their practical significance.
Latest Posts
Latest Posts
-
Student Speeches For Student Council
Sep 21, 2025
-
Label The Respiratory System Diagram
Sep 21, 2025
-
Pregabalin 150 Mg Effets Secondaires
Sep 21, 2025
-
Eight Rights For Medication Administration
Sep 21, 2025
-
What Is A Diagnostic Exam
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Is 5/16th Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.