Lcm Of 10 And 15
monicres
Sep 23, 2025 · 6 min read
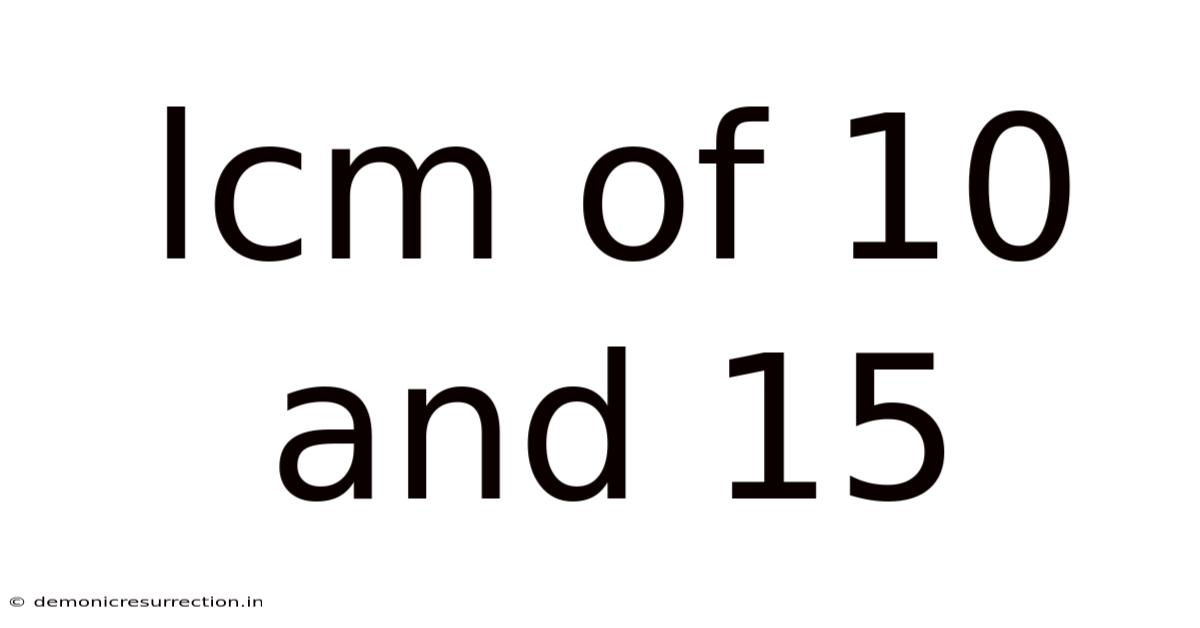
Table of Contents
Finding the LCM of 10 and 15: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will delve deep into finding the LCM of 10 and 15, explaining different methods and providing a solid understanding of the underlying principles. We'll explore the concept in detail, tackling not only the specific example but also equipping you with the skills to calculate the LCM of any two (or more) numbers.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 10 and 15, let's clarify what LCM actually means. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder.
For instance, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... and the multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially when dealing with smaller numbers like 10 and 15. We simply list out the multiples of each number until we find the smallest common multiple.
- Multiples of 10: 10, 20, 30, 40, 50, 60...
- Multiples of 15: 15, 30, 45, 60, 75...
By comparing the lists, we can see that the smallest number that appears in both lists is 30. Therefore, the LCM of 10 and 15 is 30. This method is effective for smaller numbers but becomes less practical when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then building the LCM from the prime factors. Let's break down this process for 10 and 15:
-
Find the prime factorization of each number:
- 10 = 2 x 5
- 15 = 3 x 5
-
Identify the highest power of each prime factor present in either factorization:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers of all prime factors together:
- LCM(10, 15) = 2 x 3 x 5 = 30
Therefore, the LCM of 10 and 15, using prime factorization, is 30. This method is significantly more efficient for larger numbers because it avoids the need to list out potentially lengthy sequences of multiples.
Method 3: Using the Greatest Common Divisor (GCD)
There's a powerful relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
Let's apply this to 10 and 15:
-
Find the GCD of 10 and 15:
- The factors of 10 are 1, 2, 5, and 10.
- The factors of 15 are 1, 3, 5, and 15.
- The greatest common factor is 5. Therefore, GCD(10, 15) = 5.
-
Use the formula:
- LCM(10, 15) x GCD(10, 15) = 10 x 15
- LCM(10, 15) x 5 = 150
- LCM(10, 15) = 150 / 5 = 30
Again, we find that the LCM of 10 and 15 is 30. This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more time-consuming. The Euclidean algorithm provides an efficient way to compute the GCD, especially for larger numbers.
Understanding the Significance of LCM
The LCM has numerous applications across various mathematical fields and real-world scenarios:
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, we need to find a common denominator, which is usually the LCM of the denominators. This allows us to express the fractions with a common denominator, simplifying the addition or subtraction process.
-
Scheduling Problems: The LCM is used to solve scheduling problems. For example, if two events occur at regular intervals (say, every 10 days and every 15 days), the LCM will tell us when both events will occur simultaneously again. In this case, both events would coincide every 30 days.
-
Cyclic Patterns: Many real-world phenomena exhibit cyclic patterns. The LCM helps determine when these patterns will align. Think of planetary alignments, recurring business cycles, or even the timing of traffic lights.
-
Modular Arithmetic: The concept of LCM plays a significant role in modular arithmetic, a branch of number theory with widespread applications in cryptography and computer science.
-
Algebra and Number Theory: The LCM is a fundamental building block in various advanced mathematical concepts, including solving Diophantine equations and exploring properties of number systems.
Finding the LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all prime factors from all numbers and select the highest power of each. For the GCD method, you can extend it iteratively; first find the LCM of two numbers, then find the LCM of that result and the third number, and so on. Listing multiples becomes increasingly impractical as the number of numbers increases.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all given numbers without leaving a remainder. They are inversely related; a larger GCD means a smaller LCM and vice-versa.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, if one number is a multiple of the other, the LCM will be the larger number. For instance, the LCM of 5 and 10 is 10.
Q: Is there a formula to directly calculate the LCM without using prime factorization or GCD?
A: While there isn't a single, universally efficient formula that avoids prime factorization or GCD entirely, iterative methods involving repeated divisions can be used. However, these are generally less efficient than the prime factorization or GCD methods for larger numbers.
Q: How do I find the LCM of numbers with common factors?
A: The presence of common factors simplifies the process. The methods described earlier, particularly prime factorization, efficiently handle common factors by identifying the highest power of each unique prime factor present in the factorization of all numbers.
Conclusion
Finding the LCM of 10 and 15, as we've demonstrated, isn't just about getting the answer (which is 30). It's about understanding the underlying mathematical principles and appreciating the diverse applications of this fundamental concept. Whether you use the method of listing multiples, prime factorization, or the GCD approach, the key is to choose the most efficient method based on the numbers involved. Mastering LCM calculation is a crucial step toward developing a stronger foundation in mathematics and its applications in various fields. Remember to practice regularly with different sets of numbers to reinforce your understanding and improve your problem-solving skills. The more you practice, the more intuitive this seemingly simple yet profoundly important mathematical operation will become.
Latest Posts
Latest Posts
-
G Test Port Union Route
Sep 23, 2025
-
How To Become A Professor
Sep 23, 2025
-
Convert Ml To Lbs Calculator
Sep 23, 2025
-
Sds Provide 4 Main Purposes
Sep 23, 2025
-
Diagram Of A Excretory System
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.