Square Root Of 1 9
monicres
Sep 14, 2025 · 6 min read
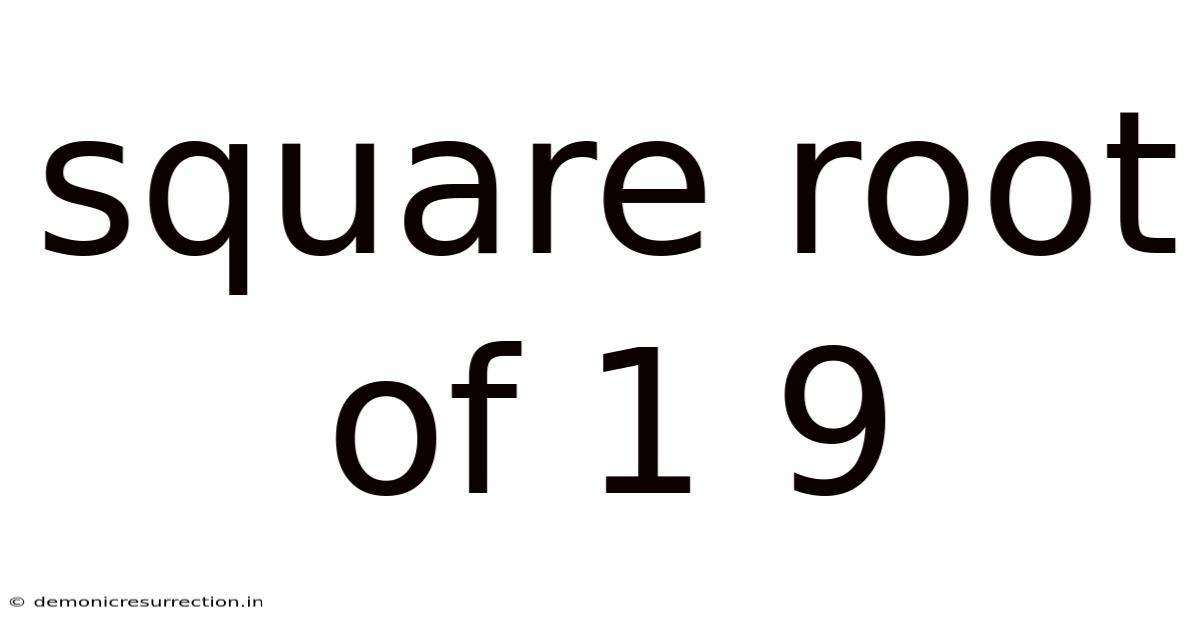
Table of Contents
Unveiling the Mysteries: Exploring the Square Root of 19
The square root of 19, denoted as √19, is a fascinating mathematical concept that often sparks curiosity. While seemingly simple, delving into its intricacies reveals a rich tapestry of mathematical principles and applications. This comprehensive guide will explore the square root of 19 from its basic definition to advanced concepts, clarifying its value, calculation methods, and practical uses. Understanding the square root of 19 isn't just about finding a number; it's about understanding the fundamental principles of mathematics and their real-world applications.
Understanding Square Roots: A Quick Refresher
Before diving into the specifics of √19, let's revisit the fundamental concept of a square root. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 multiplied by itself (3 x 3 = 9) equals 9. This concept applies to all non-negative real numbers.
Now, 19 is not a perfect square – meaning there's no whole number that, when multiplied by itself, equals 19. This implies that the square root of 19 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Calculating the Square Root of 19: Different Approaches
There are several methods to approximate the value of √19. Let's explore a few:
1. Using a Calculator: The simplest and most accurate way to find the square root of 19 is using a calculator. Most scientific calculators have a dedicated square root function (√). Simply input 19 and press the square root button. The calculator will provide a highly precise decimal approximation, typically around 4.35889894354.
2. The Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations of square roots. It starts with an initial guess and refines it through successive calculations.
- Step 1: Make an initial guess. Let's guess 4, as 4 x 4 = 16, which is close to 19.
- Step 2: Improve the guess. Divide 19 by the initial guess (19/4 = 4.75) and average this result with the initial guess: (4 + 4.75) / 2 = 4.375.
- Step 3: Repeat Step 2. Now, use 4.375 as the new guess. 19/4.375 ≈ 4.342857. Average this with 4.375: (4.375 + 4.342857) / 2 ≈ 4.3589.
- Step 4: Iterate until desired accuracy is reached. Continue this process, repeating Step 2 with each new approximation. Each iteration brings the approximation closer to the actual value of √19. The more iterations, the greater the accuracy.
3. Using Long Division Method: While less intuitive than the Babylonian method, the long division method for calculating square roots is a classic technique that demonstrates the underlying mathematical principles. This method is quite complex and requires a detailed step-by-step approach which is beyond the scope of this introductory article.
4. Using the Taylor Series Expansion: For those familiar with calculus, the Taylor series expansion can provide an accurate approximation of √19. This involves representing the square root function as an infinite sum of terms. However, this method is computationally intensive and is generally not the most practical for hand calculation.
The Irrational Nature of √19: A Deeper Dive
As mentioned earlier, √19 is an irrational number. This means its decimal representation is non-terminating and non-repeating. This is a consequence of the fact that 19 is not a perfect square. The proof of irrationality often involves the technique of proof by contradiction, assuming the number is rational and then demonstrating a logical contradiction.
Let's consider the implications of this irrationality:
- Infinite Decimal Representation: The decimal representation of √19 continues infinitely without any repeating pattern. Calculators only provide approximations to a certain number of decimal places.
- Inability to Express as a Fraction: √19 cannot be expressed as a ratio of two integers (a fraction). This is a defining characteristic of irrational numbers.
- Geometric Significance: The irrational nature of √19 has implications in geometry. For instance, if you try to construct a square with an area of 19 square units, the length of its sides would be √19, an irrational number. This means you can only approximate the side length using rational numbers.
Applications of Square Roots in General and the Relevance of √19
Square roots have widespread applications across various fields:
- Geometry: Calculating distances, areas, and volumes often involves square roots (e.g., the Pythagorean theorem). While √19 might not be a frequently encountered value in everyday geometric calculations, the principle remains the same.
- Physics: Numerous physics equations involve square roots. For example, calculating the speed of an object or the period of a pendulum.
- Engineering: Engineering designs often require precise calculations, and square roots frequently appear in formulas related to stress, strain, and other mechanical properties.
- Finance: Calculating compound interest or the present value of an investment involves the use of square roots.
- Computer Graphics: Square roots are used extensively in computer graphics and game development for calculations related to 3D transformations, rotations, and distances.
Although √19 itself might not be as commonly used as other square roots (e.g., √2, √3), its significance lies in illustrating the broader concepts of square roots, irrational numbers, and their importance in mathematical modeling and problem-solving across various fields.
Frequently Asked Questions (FAQs)
Q1: Is the square root of 19 a rational or irrational number?
A1: The square root of 19 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Q2: How can I accurately calculate the square root of 19 without a calculator?
A2: While a calculator provides the most accurate and convenient method, you can approximate √19 using methods like the Babylonian method (Heron's method) or the long division method. These iterative methods provide successively better approximations with each step.
Q3: What are the practical applications of understanding the square root of 19?
A3: Although √19 might not be encountered frequently in everyday calculations, understanding it strengthens your comprehension of square roots and irrational numbers. These concepts are fundamental in various mathematical and scientific fields, including geometry, physics, engineering, and computer science.
Q4: Why is it important to understand irrational numbers like √19?
A4: Irrational numbers, like √19, demonstrate the richness and complexity of the real number system. They are essential for accurately modeling real-world phenomena in many scientific and engineering applications where precise calculations are critical.
Q5: Can √19 be simplified further?
A5: No, √19 cannot be simplified further because 19 is a prime number and has no perfect square factors other than 1.
Conclusion: Beyond the Numbers
The square root of 19, while seemingly a simple mathematical concept, unveils a deeper understanding of fundamental mathematical principles, including irrational numbers, approximation methods, and the power of iterative calculations. Its importance extends beyond a simple numerical value. Understanding √19 and its associated concepts equips you with a stronger foundation in mathematics, enabling you to tackle more complex problems and appreciate the intricate beauty of the number system. The exploration of √19 serves as a gateway to a wider appreciation of the mathematical world and its pervasive influence on our understanding of the universe. It highlights the fact that even seemingly simple numbers can hold a wealth of mathematical depth and relevance.
Latest Posts
Latest Posts
-
Guru Nanak Dev Ji Teachings
Sep 14, 2025
-
2 000 Divided By 12
Sep 14, 2025
-
Everything Solid Melts Into Air
Sep 14, 2025
-
Rostow Stages Of Economic Growth
Sep 14, 2025
-
What Is 200ml In Cups
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.