What Is 10 Of 100
monicres
Sep 10, 2025 · 6 min read
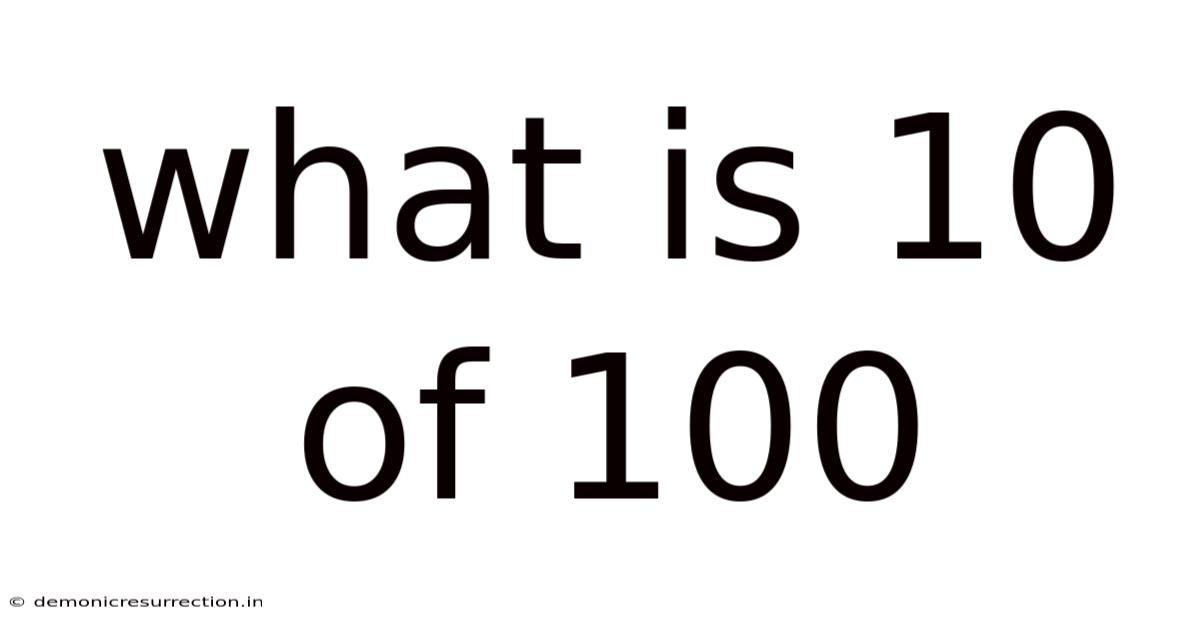
Table of Contents
What is 10 of 100? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 10 of 100?", opens a door to a fundamental concept in mathematics: understanding fractions, percentages, and ratios. While the immediate answer might seem obvious, delving deeper reveals a wealth of knowledge applicable in various fields, from everyday life to complex scientific calculations. This article will explore this seemingly simple question in depth, explaining the different mathematical interpretations and demonstrating its practical applications.
Introduction: The Multiple Facets of "10 of 100"
The phrase "10 of 100" can be interpreted in several ways, each leading to a different, yet related, mathematical representation. We can express this relationship as a fraction, a percentage, a ratio, or even a decimal. Understanding these different forms is crucial for grasping the underlying concept and applying it in various contexts. This article aims to clarify these representations and demonstrate their practical uses.
1. Understanding Fractions: The Foundation of "10 of 100"
The most straightforward interpretation of "10 of 100" is a fraction. A fraction represents a part of a whole. In this case, "10 of 100" signifies that we have 10 parts out of a total of 100 parts. This is expressed mathematically as 10/100.
-
Simplifying Fractions: Fractions can often be simplified by finding the greatest common divisor (GCD) of the numerator (the top number) and the denominator (the bottom number). The GCD of 10 and 100 is 10. Dividing both the numerator and the denominator by 10, we get the simplified fraction 1/10. This means that "10 of 100" is equivalent to one-tenth.
-
Visualizing Fractions: Imagine a pizza cut into 100 equal slices. "10 of 100" represents taking 10 of those slices. This visually demonstrates the fractional representation of the relationship between the part (10) and the whole (100).
2. Percentages: Expressing "10 of 100" as a Rate
A percentage is a way of expressing a fraction as a rate out of 100. The word "percent" literally means "per hundred." To convert the fraction 10/100 to a percentage, we simply multiply the fraction by 100%:
(10/100) * 100% = 10%
Therefore, "10 of 100" is equivalent to 10%. This is a common and widely used representation, particularly in contexts involving proportions, discounts, increases, and statistical data. Understanding percentages is crucial for interpreting data presented in charts, graphs, and reports.
3. Ratios: Comparing "10" to "100"
A ratio is a mathematical comparison of two quantities. "10 of 100" can be expressed as a ratio of 10:100, which reads as "10 to 100." Like fractions, ratios can also be simplified by dividing both numbers by their greatest common divisor. Simplifying 10:100, we get the equivalent ratio 1:10. This means that for every one part, there are ten parts in total. Ratios are extensively used in various fields, including scaling, mixing ingredients, and comparing different quantities.
4. Decimal Representation: Another Way to Express Proportion
"10 of 100" can also be represented as a decimal. To convert the fraction 10/100 to a decimal, we perform the division: 10 ÷ 100 = 0.1. This decimal, 0.1, represents one-tenth and is another way to express the proportion of 10 out of 100. Decimals are particularly useful in calculations involving measurements, monetary values, and scientific data.
Practical Applications: Where "10 of 100" is Used
The concept of "10 of 100," represented in various forms, has wide-ranging practical applications across numerous fields:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins often involves working with percentages and decimals derived from ratios like 10/100 or its equivalent forms. For example, a 10% discount on a $100 item means a reduction of $10.
-
Statistics: Statistical data is frequently presented as percentages, representing proportions of a total population or sample size. For instance, 10% of respondents in a survey might favor a particular candidate.
-
Science: Scientific experiments and measurements often involve working with proportions and ratios. A chemist might use ratios to prepare a solution, or a physicist might analyze the proportion of different elements in a compound.
-
Everyday Life: Many everyday situations involve understanding proportions. Sharing food equally, calculating cooking quantities, or measuring ingredients all rely on a conceptual grasp of fractions, ratios, and percentages.
Understanding the Interchangeability: Converting Between Representations
It is crucial to understand the interchangeability of these representations. You can easily convert between fractions, percentages, decimals, and ratios. This flexibility is a key strength in applying mathematical concepts to real-world problems.
- Fraction to Percentage: Multiply the fraction by 100%.
- Percentage to Fraction: Divide the percentage by 100% and simplify.
- Fraction to Decimal: Divide the numerator by the denominator.
- Decimal to Fraction: Write the decimal as a fraction with a denominator of a power of 10 (e.g., 0.1 = 1/10).
- Ratio to Fraction: The ratio a:b can be written as the fraction a/(a+b).
- Fraction to Ratio: The fraction a/b can be written as the ratio a:b.
Frequently Asked Questions (FAQ)
-
Q: Is there any other way to express "10 of 100"?
- A: Yes, you can also express it as a proportion (10/100), a ratio (10:100 or 1:10), or in words as "ten out of one hundred" or "one-tenth."
-
Q: What if the numbers were different? For instance, what is 25 of 100?
- A: Following the same principles, 25 of 100 is 25/100 = 1/4 = 25% = 0.25. The methods remain the same; simply substitute the different values.
-
Q: How important is understanding fractions, percentages, and ratios?
- A: Understanding these concepts is fundamental in various aspects of life and professional fields. They are essential for accurate calculations, data interpretation, and problem-solving.
-
Q: Are there any online tools or resources that can help me practice these concepts?
- A: Many online resources, including educational websites and apps, offer interactive exercises and tutorials to help you learn and practice working with fractions, percentages, and ratios.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 10 of 100?", serves as a gateway to a deeper understanding of fundamental mathematical concepts. By grasping the various representations of this relationship—as a fraction, percentage, ratio, and decimal—you equip yourself with valuable tools applicable across a wide range of fields. Mastering these concepts builds a strong foundation for more advanced mathematical studies and empowers you to confidently approach problem-solving in your daily life and professional endeavors. The ability to understand and manipulate fractions, percentages, and ratios is a crucial skill for navigating the numerical world around us. Remember the flexibility and interchangeability of these representations; this understanding is key to unlocking their full potential in various applications.
Latest Posts
Latest Posts
-
Pictures Of Hades The God
Sep 10, 2025
-
Is H2co3 A Strong Acid
Sep 10, 2025
-
The Lottery Shirley Jackson Pdf
Sep 10, 2025
-
Michel David Freres Et S Urs
Sep 10, 2025
-
Conjugation Of Lire In French
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.