What Is 15 Of 300
monicres
Sep 15, 2025 · 5 min read
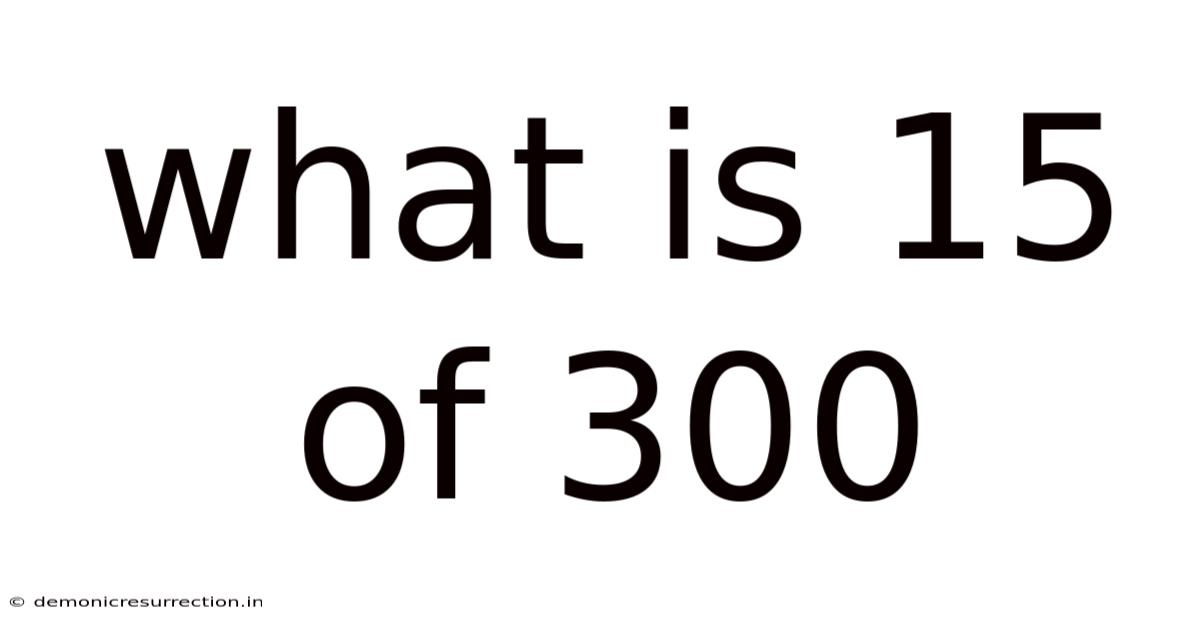
Table of Contents
What is 15% of 300? A Comprehensive Guide to Percentages
Finding a percentage of a number is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will thoroughly explore how to calculate 15% of 300, providing multiple methods to understand the process and its underlying principles. We'll delve into the basic concepts of percentages, explore different calculation methods, and address frequently asked questions, ensuring a comprehensive understanding for learners of all levels. This guide aims to be your go-to resource for understanding percentages, making this seemingly simple calculation a stepping stone to mastering more complex mathematical concepts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred" or "out of one hundred." Therefore, 15% can be written as the fraction 15/100 or the decimal 0.15. Understanding this fundamental relationship is key to solving percentage problems.
The crucial concept to grasp is that percentages represent a proportional relationship. 15% of 300 means finding 15 parts out of every 100 parts of 300. This concept applies to any number, making percentages a universal tool for comparing and analyzing proportions.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
-
Step 1: Convert the percentage to a decimal. To do this, divide the percentage by 100. So, 15% becomes 15/100 = 0.15.
-
Step 2: Multiply the decimal by the number. In our case, we multiply 0.15 by 300: 0.15 * 300 = 45.
Therefore, 15% of 300 is $\boxed{45}$.
Method 2: Using the Fraction Equivalent
This method uses the fraction representation of the percentage.
-
Step 1: Convert the percentage to a fraction. 15% is equivalent to the fraction 15/100.
-
Step 2: Simplify the fraction (if possible). The fraction 15/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 5. This simplifies to 3/20.
-
Step 3: Multiply the simplified fraction by the number. We multiply 3/20 by 300: (3/20) * 300 = (3 * 300) / 20 = 900 / 20 = 45.
Again, we find that 15% of 300 is $\boxed{45}$.
Method 3: Using Proportions
This method uses the concept of proportionality to solve the problem.
We can set up a proportion:
15/100 = x/300
Where 'x' represents 15% of 300. To solve for x, we cross-multiply:
15 * 300 = 100 * x
4500 = 100x
x = 4500 / 100
x = 45
This confirms that 15% of 300 is $\boxed{45}$.
Method 4: Breaking Down the Percentage
This method involves calculating smaller percentages and adding them together. While potentially more time-consuming for simple calculations, it can be helpful for understanding the underlying proportional relationships and is useful for mental calculations of more complex percentages.
We can break down 15% into 10% and 5%.
-
10% of 300: 10% is equivalent to 1/10. Therefore, 1/10 * 300 = 30.
-
5% of 300: 5% is half of 10%, so 5% of 300 is 30 / 2 = 15.
-
Adding the results: 30 (10%) + 15 (5%) = 45.
This demonstrates that 15% of 300 is $\boxed{45}$.
The Significance of Understanding Percentages
Beyond simply calculating 15% of 300, understanding percentages is crucial for various aspects of life:
-
Financial Literacy: Calculating discounts, sales tax, interest rates, tips, and investment returns all rely on understanding percentages.
-
Data Analysis: Percentages are fundamental to interpreting statistical data, allowing for easy comparison of proportions across different datasets. This is vital in fields like economics, market research, and healthcare.
-
Everyday Calculations: From understanding nutritional information on food labels to comprehending sale prices in stores, percentages are ubiquitous in daily life.
-
Advanced Mathematics: Percentages form the basis for more advanced mathematical concepts, including compound interest, exponential growth, and probability.
Frequently Asked Questions (FAQ)
Q1: How can I calculate percentages without a calculator?
A1: For simple percentages like 10%, 25%, and 50%, mental calculations are easy. You can also use the fraction method, breaking down percentages into simpler components, as demonstrated in Method 4. Practice with various examples builds confidence in performing mental calculations.
Q2: What if I need to calculate a different percentage of 300?
A2: The methods outlined above can be applied to any percentage. Simply replace "15" with your desired percentage and follow the steps.
Q3: Are there online tools to calculate percentages?
A3: Yes, many online calculators are readily available. However, understanding the underlying principles is crucial for applying percentage calculations effectively in various contexts. Relying solely on calculators without grasping the concepts limits your ability to solve more complex percentage-related problems.
Q4: What are some real-world examples where calculating percentages is important?
A4: Consider these examples: calculating the discount on a sale item (e.g., 20% off a $100 item), determining the sales tax added to a purchase, figuring out the tip amount at a restaurant, understanding interest earned on a savings account, or analyzing the success rate of a marketing campaign.
Q5: Can percentages be greater than 100%?
A5: Yes, percentages can exceed 100%. This signifies that a value is greater than the original value being compared to. For instance, if a company's profits increased by 120% compared to the previous year, it means the profits are now 220% of the previous year's profits.
Conclusion
Calculating 15% of 300, which equals 45, is a straightforward process once you understand the underlying principles of percentages. Whether using the decimal equivalent, fraction method, proportions, or breaking down the percentage, the result remains consistent. Mastering this seemingly simple calculation provides a strong foundation for tackling more complex percentage problems and empowers you with a valuable skill applicable in various aspects of life and across multiple disciplines. Remember that the key is not just memorizing formulas but also understanding the fundamental concepts of ratios and proportions. Practice is key to building confidence and proficiency in working with percentages.
Latest Posts
Latest Posts
-
7 4 As A Percent
Sep 15, 2025
-
Leave In The Past Simple
Sep 15, 2025
-
1 7 8 In To Mm
Sep 15, 2025
-
Difference Between Archaebacteria And Eubacteria
Sep 15, 2025
-
Definition Of A Plane Mirror
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.