What Is 25 Of 75
monicres
Sep 15, 2025 · 4 min read
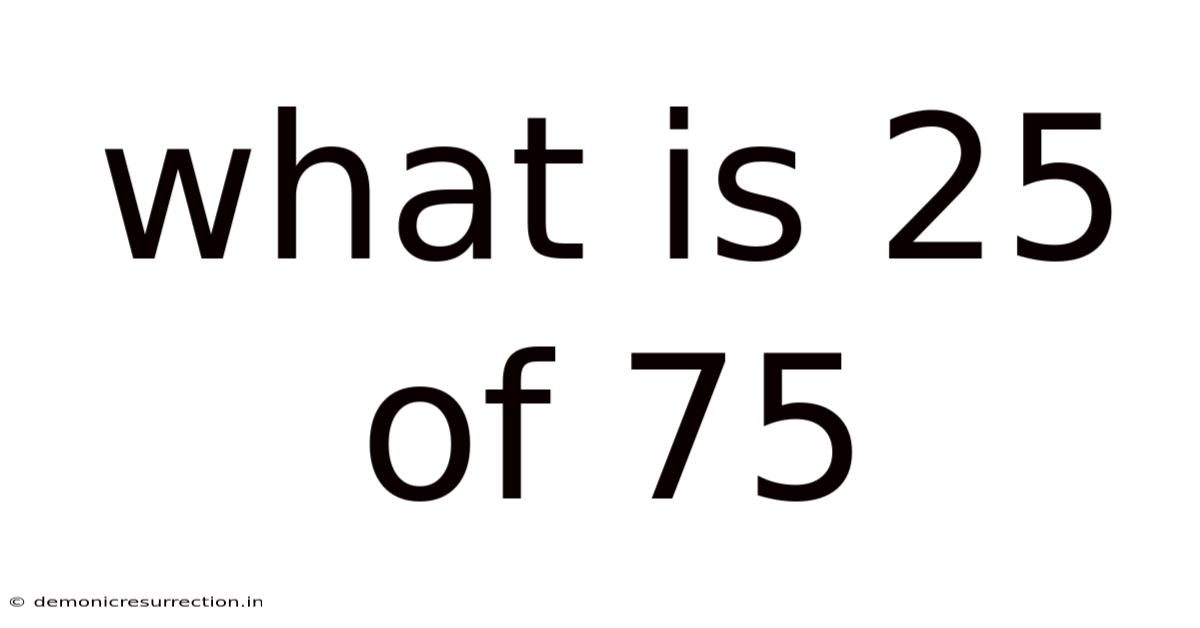
Table of Contents
What is 25 of 75? Unpacking Percentages, Fractions, and Ratios
This seemingly simple question, "What is 25 of 75?", opens a door to a deeper understanding of fundamental mathematical concepts. It's not just about finding a numerical answer; it's about grasping the relationships between percentages, fractions, and ratios – skills crucial for everyday life and advanced mathematical studies. This article will comprehensively explore this question, providing multiple approaches to solving it and delving into the underlying mathematical principles.
Understanding the Question
The phrase "25 of 75" implies a part-to-whole relationship. We're looking for the proportion that 25 represents when compared to the whole, 75. This proportion can be expressed in several ways: as a fraction, a decimal, or a percentage.
Method 1: Using Fractions
The most straightforward method is to express the relationship as a fraction: 25/75. This fraction represents 25 parts out of a total of 75 parts. To simplify this fraction, we find the greatest common divisor (GCD) of 25 and 75, which is 25. Dividing both the numerator and the denominator by 25 gives us:
25/75 = 1/3
Therefore, 25 is one-third (1/3) of 75.
Method 2: Using Decimals
To express the fraction 1/3 as a decimal, we perform the division:
1 ÷ 3 ≈ 0.3333...
The decimal representation of 1/3 is a repeating decimal, meaning the digit 3 repeats infinitely. For practical purposes, we often round this to a certain number of decimal places, such as 0.33 or 0.333.
Method 3: Using Percentages
A percentage represents a fraction out of 100. To convert the fraction 1/3 to a percentage, we can set up a proportion:
1/3 = x/100
To solve for x, we cross-multiply:
3x = 100 x = 100/3 ≈ 33.33...
Therefore, 25 is approximately 33.33% of 75. Again, we often round this to a more manageable number, such as 33.3% or 33%.
Deeper Dive: Proportions and Ratios
The problem "What is 25 of 75?" fundamentally deals with proportions and ratios. A ratio compares two quantities, while a proportion states that two ratios are equal. We can express the relationship between 25 and 75 as a ratio: 25:75. This ratio simplifies to 1:3, which is equivalent to the fraction 1/3.
Understanding proportions is crucial in many real-world applications, such as:
- Scaling recipes: If a recipe calls for 25 grams of sugar for 75 grams of flour, and you want to make a smaller batch, you can use proportions to determine the correct amounts of each ingredient.
- Map scales: Maps use proportions to represent distances on a smaller scale. For example, a map scale might indicate that 1 cm represents 10 km.
- Calculating discounts: A 25% discount on a $75 item can be calculated using proportions.
Practical Applications and Examples
Let's explore a few real-world scenarios where understanding "25 of 75" comes in handy:
- Sales and Discounts: A store offers a discount of $25 on an item originally priced at $75. This represents a 1/3 discount, or approximately 33.33%.
- Survey Results: If 25 out of 75 people surveyed prefer a particular brand, this represents 1/3 or approximately 33.33% of the respondents.
- Inventory Management: A warehouse has 75 units of a product, and 25 are sold. This means 1/3 or approximately 33.33% of the inventory has been sold.
- Grade Calculation: If a student correctly answers 25 out of 75 questions on a test, their score is 1/3 or approximately 33.33%.
Beyond the Basics: Expanding Your Understanding
This seemingly simple problem lays the foundation for more complex mathematical concepts. Here's how it connects to other areas:
- Probability: The fraction 1/3 can represent the probability of a certain event occurring.
- Statistics: Percentages and proportions are fundamental to statistical analysis.
- Algebra: Solving proportions often involves algebraic equations.
- Geometry: Ratios are used extensively in geometry, particularly in similar figures.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, a calculator can be used to convert the fraction 25/75 to a decimal (0.333...) and then to a percentage (approximately 33.33%).
-
Q: What if the numbers weren't so easily divisible? A: If the numbers were less easily simplified, you'd still use the same process – create the fraction, simplify it as much as possible, and then convert it to a decimal or percentage. Calculators become increasingly helpful in these instances.
-
Q: Is it always necessary to simplify the fraction? A: While simplifying is generally good practice for clarity and ease of understanding, it's not strictly necessary. The unsimplified fraction 25/75 still represents the same proportion as 1/3.
-
Q: Are there other ways to express this proportion? A: Yes, you could use a ratio (25:75 or 1:3) or a decimal (0.333...). The best representation depends on the context.
Conclusion: The Power of Proportion
The seemingly simple question, "What is 25 of 75?", provides a rich learning opportunity. It emphasizes the interconnectedness of fractions, decimals, percentages, ratios, and proportions – fundamental mathematical concepts with broad applications in various fields. Mastering these concepts strengthens your analytical abilities and problem-solving skills, equipping you to tackle more complex challenges. By understanding the underlying principles and practicing various methods, you can confidently navigate similar problems and appreciate the power of proportion in everyday life.
Latest Posts
Latest Posts
-
Example Of A Persuasive Essay
Sep 15, 2025
-
What Is Is In German
Sep 15, 2025
-
Inverse Of An Exponential Function
Sep 15, 2025
-
1 72 M Height In Feet
Sep 15, 2025
-
The Turner Diaries William Pierce
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.