What Is 30 Of 1000
monicres
Sep 17, 2025 · 5 min read
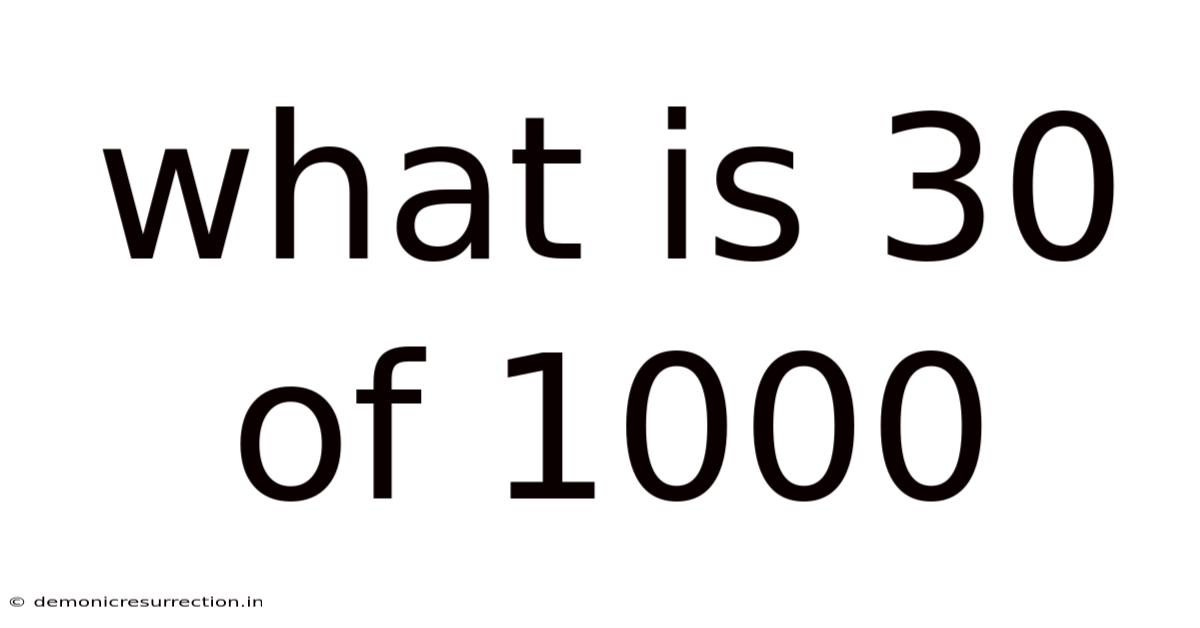
Table of Contents
What is 30 of 1000? Understanding Percentages, Fractions, and Ratios
Finding "30 of 1000" might seem like a simple arithmetic problem, but it opens the door to understanding fundamental mathematical concepts like percentages, fractions, and ratios. This seemingly straightforward question allows us to explore these concepts in detail and apply them to various real-world scenarios. This article will guide you through calculating "30 of 1000," explaining the process step-by-step and exploring the broader implications of this type of calculation.
Understanding the Question
The question "What is 30 of 1000?" essentially asks us to determine what portion 30 represents out of a total of 1000. This can be interpreted in several ways, each leading to a different but equally valid answer depending on the desired format. We can express this relationship as a fraction, a decimal, a percentage, or even a ratio.
Method 1: Calculating the Fraction
The most straightforward approach is to express the relationship as a fraction. "30 of 1000" can be written as the fraction 30/1000. This fraction represents the part (30) over the whole (1000). To simplify this fraction, we find the greatest common divisor (GCD) of 30 and 1000, which is 10. Dividing both the numerator and the denominator by 10, we get:
30/1000 = 3/100
This simplified fraction, 3/100, indicates that 30 out of 1000 represents three parts out of every hundred.
Method 2: Converting to a Decimal
To convert the fraction 3/100 to a decimal, we simply divide the numerator (3) by the denominator (100):
3 ÷ 100 = 0.03
Therefore, 30 out of 1000 is equal to 0.03. This decimal representation is particularly useful in calculations and comparisons, especially when dealing with larger datasets or when using computers for analysis.
Method 3: Calculating the Percentage
Percentages are a common way of expressing proportions. To convert the fraction 3/100 (or the decimal 0.03) to a percentage, we multiply by 100 and add the "%" symbol:
(3/100) × 100% = 3%
Alternatively, from the decimal:
0.03 × 100% = 3%
This means that 30 out of 1000 represents 3% of the total. Percentages are easily understood and widely used to represent proportions in various contexts, from financial reports to scientific data.
Method 4: Expressing as a Ratio
A ratio expresses the relationship between two quantities. In this case, the ratio of 30 to 1000 can be written as:
30:1000
This ratio can be simplified by dividing both numbers by their GCD (10):
3:100
This simplified ratio, 3:100, means that for every 100 items, 3 are of the specified type. Ratios are frequently used in fields like scaling, mixing, and comparing proportions in different contexts.
Real-World Applications
Understanding how to calculate "30 of 1000" and express it in different formats has numerous practical applications:
-
Financial Calculations: Imagine you have 1000 shares of a company, and 30 of them are sold. Calculating the percentage of shares sold helps in financial analysis.
-
Survey Results: If 30 out of 1000 respondents chose a particular option in a survey, expressing this as a percentage gives a clear representation of public opinion.
-
Statistical Analysis: In statistical analysis, proportions are frequently calculated and expressed as percentages or decimals.
-
Production and Quality Control: If 30 out of 1000 products are defective, the percentage of defective items helps in quality control measures.
-
Recipe Scaling: If a recipe calls for 30 grams of an ingredient out of a total of 1000 grams of ingredients, it's easy to adjust the recipe proportionally for different batch sizes.
Expanding the Concept: Proportional Reasoning
The calculation of "30 of 1000" is a fundamental example of proportional reasoning. Proportional reasoning is the ability to understand and work with ratios and proportions. This skill is crucial in many areas, including:
-
Problem Solving: Solving many real-world problems involves setting up and solving proportions.
-
Data Interpretation: Interpreting data often involves understanding and analyzing proportions.
-
Decision Making: Many decisions require understanding the proportional relationships between different factors.
Beyond the Basics: More Complex Proportions
While "30 of 1000" is a simple case, the principles extend to more complex scenarios. Imagine you needed to find a certain percentage of a different number, or solve for an unknown part of a proportion. This requires applying the fundamental concepts discussed above. For example:
-
Finding a Percentage of a Number: To find 5% of 700, we would calculate (5/100) * 700 = 35.
-
Solving for an Unknown Part: If we know that x% of 800 is 20, we could set up a proportion: x/100 = 20/800, solve for x to find the percentage (x = 2.5%).
-
More Complex Ratios: Ratios can involve more than two quantities. For instance, a ratio of 2:3:5 represents a proportional distribution among three parts.
Frequently Asked Questions (FAQ)
-
Q: What if I need to find 300 of 1000?
- A: Follow the same steps: the fraction would be 300/1000, which simplifies to 3/10, a decimal of 0.3, and a percentage of 30%.
-
Q: How can I calculate this without a calculator?
- A: For simple fractions like 30/1000, simplifying by dividing both numerator and denominator by their GCD is often easy to do mentally. For more complex calculations, pencil and paper can be used for long division.
-
Q: Why are percentages so useful?
- A: Percentages provide a standardized way to compare proportions. They make it easy to understand relative sizes, making data analysis and comparison easier.
Conclusion
Determining "what is 30 of 1000" involves more than just a simple calculation. It offers a gateway to understanding core mathematical concepts: fractions, decimals, percentages, and ratios. Mastering these concepts is essential for navigating various aspects of life, from everyday problem-solving to advanced mathematical and scientific pursuits. By understanding these fundamentals and practicing proportional reasoning, you can confidently tackle more complex proportional problems and analyze data effectively. Remember that each method – fraction, decimal, percentage, and ratio – offers a different but equally valid way to represent the relationship between 30 and 1000, allowing you to choose the most appropriate method depending on the context.
Latest Posts
Latest Posts
-
Example Of Proportion In Art
Sep 17, 2025
-
My Husband Is Hitting Me
Sep 17, 2025
-
Difference Between Mixture And Compound
Sep 17, 2025
-
How To Combine Unlike Terms
Sep 17, 2025
-
100 Acres En Pieds Carres
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.