What Is 30 Of 75
monicres
Sep 04, 2025 · 5 min read
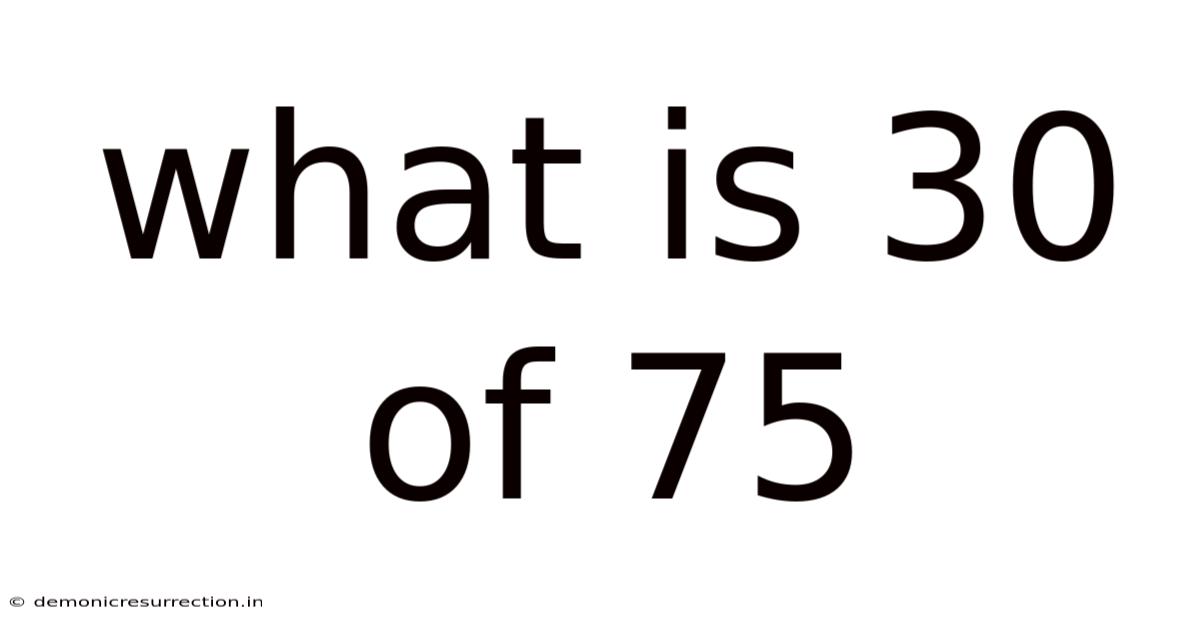
Table of Contents
What is 30 of 75? Understanding Fractions, Percentages, and Ratios
What is 30 out of 75? This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. While the answer itself is straightforward, exploring the different methods to solve it and the broader implications of these calculations provides valuable insights into everyday problem-solving. This article will delve into various approaches to answering this question, emphasizing practical applications and building a solid foundation in mathematical reasoning.
Understanding the Problem: Fractions, Percentages, and Ratios
At its core, "30 of 75" represents a fractional part of a whole. We can express this relationship in several ways:
-
Fraction: The simplest representation is the fraction 30/75. This indicates that 30 is a part of a larger whole, 75.
-
Percentage: Percentages express a fraction as a part of 100. We can convert the fraction 30/75 into a percentage to understand what proportion of 75 is represented by 30.
-
Ratio: A ratio compares two quantities. In this case, the ratio is 30:75, indicating the relationship between 30 and 75.
Method 1: Simplifying the Fraction
The most direct approach to solving "30 of 75" involves simplifying the fraction 30/75. This means finding the greatest common divisor (GCD) of both the numerator (30) and the denominator (75) and dividing both by that number.
-
Find the GCD: The GCD of 30 and 75 is 15. This means both numbers are divisible by 15.
-
Simplify: Divide both the numerator and denominator by 15:
30 ÷ 15 = 2 75 ÷ 15 = 5
-
Result: The simplified fraction is 2/5. This means 30 is 2/5 of 75.
Method 2: Converting to a Percentage
Converting the fraction to a percentage provides a more intuitive understanding of the proportion. The process involves:
-
Divide the numerator by the denominator: 30 ÷ 75 = 0.4
-
Multiply by 100: 0.4 × 100 = 40%
-
Result: 30 is 40% of 75.
Method 3: Using Decimal Representation
We can also work with decimal representation directly. The fraction 30/75, as we've seen, simplifies to 2/5. Converting 2/5 to a decimal, we get:
2 ÷ 5 = 0.4
This decimal, 0.4, can then be easily converted to a percentage by multiplying by 100 (0.4 x 100 = 40%).
Method 4: Proportions and Cross-Multiplication
This method is particularly useful when dealing with more complex problems involving proportions. We can set up a proportion:
30/75 = x/100
Where 'x' represents the percentage. Cross-multiplying gives us:
30 × 100 = 75 × x
3000 = 75x
x = 3000 ÷ 75 = 40
Therefore, x = 40%, confirming our previous results.
Real-World Applications: Why This Matters
Understanding how to calculate "30 of 75" and its equivalents extends far beyond simple arithmetic. Here are a few practical applications:
-
Calculating Discounts: Imagine a store offering a 40% discount on an item priced at $75. Knowing that 40% of 75 is 30, you can quickly determine the discount amount ($30).
-
Grading and Assessment: If you scored 30 out of 75 on a test, you can easily calculate your percentage score (40%). This allows for easy comparison with other students and helps understand your performance.
-
Data Analysis: In various fields, from finance to science, understanding proportions is crucial for interpreting data. For example, if 30 out of 75 participants in a survey responded positively, this represents 40% positive responses.
-
Recipe Scaling: If a recipe calls for 75 grams of flour and you only want to make a smaller portion, calculating 30 grams (40% of 75 grams) allows you to accurately scale down the recipe.
-
Budgeting: If your monthly budget is $75 and you allocate $30 for entertainment, you've allocated 40% of your budget to entertainment.
Beyond the Basics: Further Exploration of Fractions, Percentages, and Ratios
While solving "30 of 75" provides a basic understanding of these concepts, it's important to explore their complexities further:
-
Complex Fractions: Dealing with fractions within fractions can be more challenging but essential in advanced mathematical applications.
-
Percentage Increase and Decrease: Calculating percentage changes is crucial for understanding growth or decline in various contexts, like population growth or economic fluctuations.
-
Ratio and Proportion Problems: Solving problems involving proportions requires understanding the relationship between different quantities and applying techniques like cross-multiplication.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 30/75?
A: The simplest form is 2/5.
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to perform the division (30 ÷ 75) and then multiply by 100 to convert to a percentage.
Q: What if the numbers were larger? Would the methods still apply?
A: Absolutely. The principles of simplifying fractions, converting to percentages, and using proportions remain the same, regardless of the size of the numbers.
Q: Are there other ways to express the relationship between 30 and 75?
A: Yes, you can express it as a ratio (30:75), a decimal (0.4), or a percentage (40%).
Q: Why is understanding fractions, percentages, and ratios important?
A: These concepts are fundamental to numerous aspects of everyday life, from finance and budgeting to data analysis and problem-solving. They are building blocks for more advanced mathematical concepts.
Conclusion: Mastering Fundamental Mathematical Concepts
The question "What is 30 of 75?" may seem simple, but it serves as a gateway to understanding the fundamental concepts of fractions, percentages, and ratios. Mastering these concepts is crucial not only for academic success but also for navigating everyday life. By exploring the different methods of calculation and understanding their practical applications, you build a solid foundation for more advanced mathematical reasoning and problem-solving skills. The ability to confidently tackle such problems equips you with valuable tools for success in various aspects of life. Remember to practice these methods with different numbers to reinforce your understanding and build confidence in your mathematical abilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 30 Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.