What Is 30 Of 90
monicres
Sep 18, 2025 · 5 min read
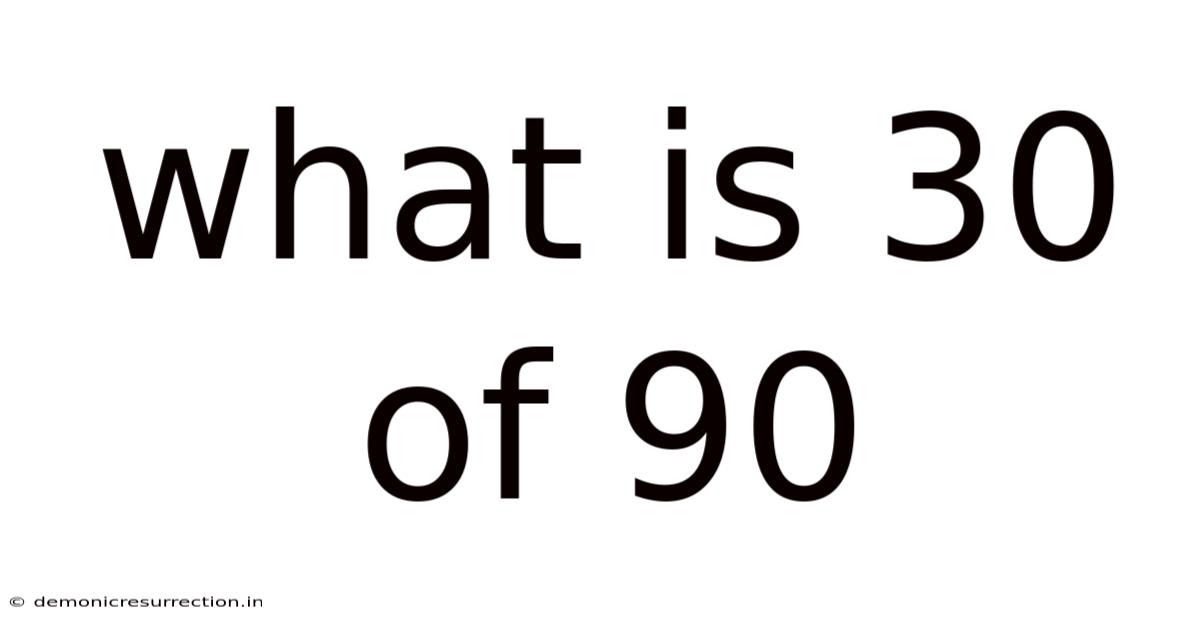
Table of Contents
What is 30 of 90? Understanding Fractions, Percentages, and Ratios
The seemingly simple question, "What is 30 of 90?" actually opens the door to understanding several fundamental mathematical concepts: fractions, percentages, and ratios. This article will delve into each of these, explaining how they relate to the question and providing practical examples to solidify your understanding. We will explore different ways to interpret and solve this problem, highlighting the versatility of mathematical tools in everyday situations.
Introduction: Deconstructing the Question
The phrase "30 of 90" can be interpreted in several ways, each leading to a different but related mathematical operation. It fundamentally asks us to express the relationship between the number 30 and the number 90. This relationship can be expressed as a fraction, a percentage, or a ratio, all of which are interconnected. This article will explore each of these representations and their applications.
1. Understanding Fractions: 30/90
The most straightforward interpretation of "30 of 90" is as a fraction. A fraction represents a part of a whole. In this case, 30 represents the part, and 90 represents the whole. Therefore, the fraction is written as 30/90.
-
Simplifying the Fraction: Fractions are often simplified to their lowest terms. To simplify 30/90, we find the greatest common divisor (GCD) of 30 and 90, which is 30. Dividing both the numerator (30) and the denominator (90) by 30 gives us:
30 ÷ 30 / 90 ÷ 30 = 1/3
This means that 30 is one-third of 90.
2. Calculating Percentages: Converting Fractions to Percentages
A percentage is a way of expressing a fraction as a proportion of 100. To convert the fraction 1/3 to a percentage, we perform the following calculation:
(1/3) x 100% = 33.33% (approximately)
Therefore, 30 is approximately 33.33% of 90. The percentage shows the proportional relationship between the two numbers, making it easy to understand the relative size of one number compared to the other. This is frequently used in various applications, such as calculating discounts, determining grades, and analyzing statistical data.
3. Exploring Ratios: Expressing the Relationship
A ratio expresses the relative size of two or more values. The ratio of 30 to 90 can be written as 30:90 or 30/90. Similar to fractions, ratios can be simplified. Simplifying the ratio 30:90 by dividing both numbers by their GCD (30) gives us the simplified ratio 1:3. This means for every one unit of the first value, there are three units of the second value. Ratios are extensively used in various fields, such as comparing quantities, scaling models, and determining proportions in recipes or mixtures.
4. Practical Applications: Real-World Examples
Understanding fractions, percentages, and ratios is essential in numerous everyday situations:
- Shopping: Imagine a sale offering a 33% discount on an item priced at $90. Using our knowledge, you can quickly calculate the discount as ($90 * 0.33) = $29.70.
- Cooking: A recipe calls for a 1:3 ratio of sugar to flour. If you use 30 grams of sugar, you'll need 90 grams of flour.
- Grades: If you answered 30 questions correctly out of 90, your score is 33.33%.
- Surveys: If 30 out of 90 respondents answered “yes” to a particular question, the percentage of “yes” responses is 33.33%.
5. Expanding the Understanding: Beyond the Basics
The question "What is 30 of 90?" allows us to explore concepts beyond simple calculation. Consider these extensions:
- Inverse Proportion: If we know 30 is 1/3 of 90, we can also determine that 90 is three times 30. This demonstrates the inverse relationship between the two numbers.
- Proportional Reasoning: We can use this understanding to solve other proportional problems. For example, if 30 represents 1/3 of a certain quantity, what would 60 represent? The answer is 2/3. This type of reasoning is crucial in various mathematical and scientific contexts.
- Percentage Increase/Decrease: We can also analyze this in terms of percentage change. If a quantity increases from 30 to 90, the percentage increase is calculated as [(90-30)/30] * 100% = 200%.
6. Addressing Common Misconceptions
- Confusing Fractions and Ratios: While closely related, fractions and ratios have subtle differences. A fraction represents a part of a whole, while a ratio compares two or more quantities. Both 30/90 and 30:90 represent the same relationship but have different interpretations.
- Incorrect Simplification: Failure to simplify fractions or ratios can lead to inaccurate results and make further calculations more difficult. Always simplify to the lowest terms for clarity and efficiency.
- Rounding Errors: When converting fractions to percentages, rounding may introduce small errors. It's essential to understand that 33.33% is an approximation of 1/3.
7. Frequently Asked Questions (FAQ)
- Q: Can I use a calculator to solve this? A: Yes, a calculator can simplify fractions and convert fractions to percentages. However, understanding the underlying concepts is crucial for applying these calculations to different contexts.
- Q: What if the numbers are larger or more complex? A: The same principles apply. Find the GCD to simplify the fraction or ratio, then convert to a percentage if needed.
- Q: Are there other ways to represent the relationship between 30 and 90? A: Yes, you could use decimal representation (0.333…), which is equivalent to 1/3.
8. Conclusion: Mastering the Fundamentals
The question, "What is 30 of 90?" provides a simple yet effective entry point into the world of fractions, percentages, and ratios. Mastering these fundamental concepts is crucial not only for academic success but also for navigating everyday life and solving practical problems in various fields. This article has explored the interconnectedness of these mathematical tools, showcasing their versatility and importance in interpreting and understanding numerical relationships. By practicing these concepts and understanding their applications, you will develop a strong foundation for more advanced mathematical explorations. Remember, the key is to understand the underlying concepts, not just the mechanics of the calculations. With practice and a firm grasp of these principles, you'll confidently tackle similar problems and appreciate the power of these fundamental mathematical tools.
Latest Posts
Latest Posts
-
Key Signatures In Bass Clef
Sep 18, 2025
-
Clb 7 In French Means
Sep 18, 2025
-
Words To Mexican National Anthem
Sep 18, 2025
-
Convert 86 F To Celsius
Sep 18, 2025
-
Vegetables And Fruits In French
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.