What Is 5 Of 20
monicres
Sep 15, 2025 · 6 min read
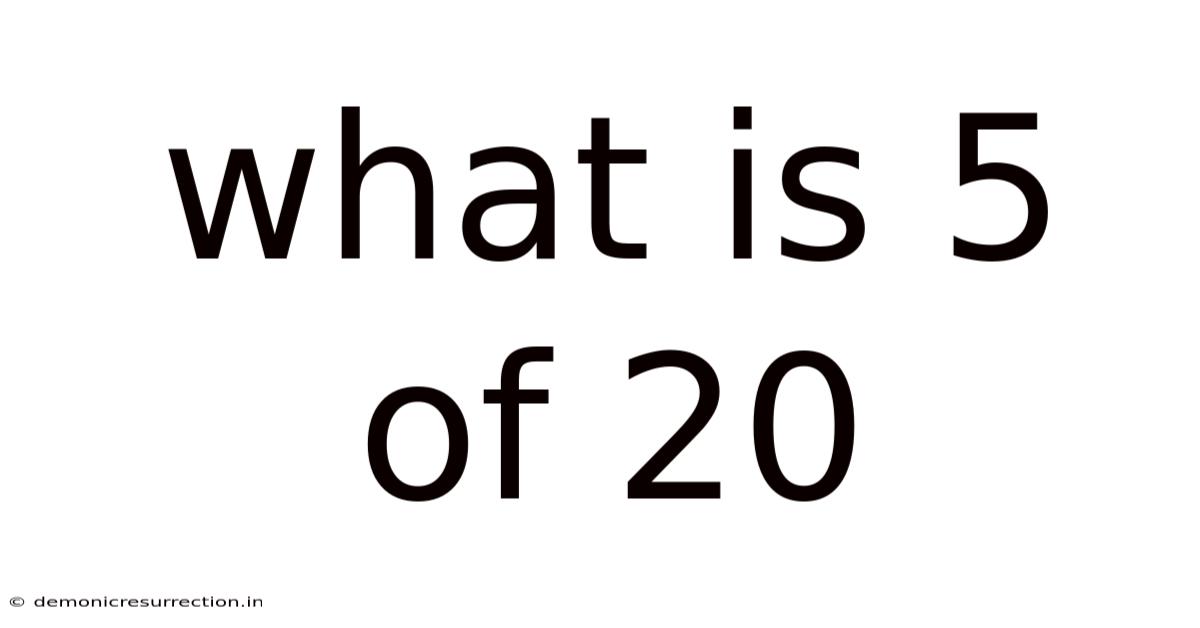
Table of Contents
What is 5 of 20? Unpacking Fractions, Percentages, and Ratios
Understanding "5 of 20" might seem simple at first glance, but it opens a door to a fundamental concept in mathematics: representing parts of a whole. This seemingly basic phrase introduces us to the world of fractions, percentages, and ratios, all crucial tools for navigating everyday life and more complex mathematical problems. This article will delve deep into the meaning of "5 of 20," exploring its different interpretations and demonstrating its application in various contexts.
Understanding the Core Concept: Parts of a Whole
At its heart, "5 of 20" signifies that we're dealing with a portion of a larger quantity. We have a total of 20 items, and we're focusing on 5 of those items. This relationship can be expressed in several ways, each with its own advantages depending on the context.
1. Fractions: Representing Parts as a Relationship
The most direct way to represent "5 of 20" is as a fraction: 5/20. A fraction shows a part (the numerator, 5 in this case) in relation to the whole (the denominator, 20). This fraction represents 5 out of a total of 20 units.
-
Simplifying Fractions: The fraction 5/20 can be simplified. Both the numerator (5) and the denominator (20) are divisible by 5. Dividing both by 5 gives us the equivalent fraction 1/4. This simplification doesn't change the value; it just presents it in a more concise form. Both 5/20 and 1/4 represent the same portion of the whole.
-
Visualizing Fractions: Imagine a pizza cut into 20 equal slices. "5 of 20" represents taking 5 of those slices. The simplified fraction, 1/4, shows that this is equivalent to taking one-quarter of the entire pizza. This visual representation helps solidify the concept of fractions and their relationship to parts of a whole.
2. Percentages: Expressing Parts as a Proportion of 100
Percentages offer another way to represent "5 of 20." A percentage expresses a fraction as a proportion of 100. To convert the fraction 5/20 (or its simplified form 1/4) into a percentage, we perform the following calculation:
(5/20) * 100% = 25%
Therefore, "5 of 20" is equivalent to 25%. This means that 5 represents 25% of the total quantity of 20. Percentages are particularly useful for comparing proportions, making them invaluable in various fields, from finance to statistics.
3. Ratios: Comparing Two Quantities
A ratio expresses the relative size of two quantities. In the context of "5 of 20," we can express the ratio of the part (5) to the whole (20) as 5:20. This ratio can also be simplified, just like fractions, by dividing both numbers by their greatest common divisor (5), resulting in the simplified ratio 1:4.
-
Interpreting Ratios: The ratio 1:4 indicates that for every 1 unit of the part, there are 4 units of the whole. This is consistent with the fraction 1/4 and the percentage 25%. Ratios are particularly helpful when comparing different quantities or proportions, allowing us to see relative relationships clearly.
-
Applications of Ratios: Ratios are widely used in various fields like cooking (e.g., mixing ingredients), construction (e.g., scaling blueprints), and finance (e.g., calculating investment returns).
Practical Applications of "5 of 20"
The concept of "5 of 20" isn't just an abstract mathematical idea; it finds practical application in numerous everyday scenarios:
-
Surveys and Statistics: If a survey of 20 people shows that 5 prefer a particular product, the result can be expressed as a fraction (1/4), percentage (25%), or ratio (1:4), providing a clear picture of consumer preference.
-
Inventory Management: If a warehouse has 20 units of a specific item and 5 are sold, the remaining inventory can be expressed using fractions, percentages, or ratios to monitor stock levels.
-
Probability and Chance: If you have 20 marbles, 5 of which are red, the probability of picking a red marble at random is 5/20, or 1/4 (25%).
-
Budgeting: If you allocate 20% of your budget to a certain expense and the total budget is $100, then 20% of $100 ($20) is allocated to that expense. Understanding percentages and fractions allows you to manage your budget more effectively.
-
Test Scores: If you answered 5 questions correctly out of a total of 20 questions on a test, your score is 25%.
Beyond the Basics: Extending the Understanding
Understanding "5 of 20" paves the way to grasping more complex mathematical concepts:
-
Proportions: Proportions involve finding equivalent ratios or fractions. For example, if 5 out of 20 students in a class like math, how many students would like math out of a class of 100 students? This is a proportion problem solved by setting up an equation and solving for the unknown.
-
Decimals: Fractions can easily be converted into decimals. The fraction 5/20 (or 1/4) is equal to 0.25. Decimals offer another way to represent parts of a whole, which is particularly useful in calculations involving money or measurements.
-
Advanced Statistics: Understanding fractions, percentages, and ratios is foundational for more advanced statistical concepts like probability distributions and hypothesis testing.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to understand "5 of 20"?
A: The easiest way is to visualize it. Imagine 20 objects, and then select 5 of them. This directly represents the core concept of a part of a whole.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and compare. It also makes subsequent calculations simpler.
Q: Can "5 of 20" be expressed in other ways besides fractions, percentages, and ratios?
A: While these three are the most common and mathematically precise ways, you could also describe it verbally as "one-quarter" or "25 percent" or "five out of twenty". However, fractions, percentages, and ratios offer a more concise and standardized way of representing the information.
Q: What if the numbers are larger? Does the principle change?
A: No, the principle remains the same. Regardless of the size of the numbers, you are still representing a part (numerator) in relation to a whole (denominator). You can always use fractions, percentages, and ratios to represent the relationship between the two numbers.
Conclusion: Mastering the Fundamentals
Understanding "5 of 20" is far more than just knowing the answer; it's about understanding the fundamental concepts of fractions, percentages, and ratios. These mathematical tools are essential not only for academic success but also for navigating everyday life, making informed decisions, and building a strong foundation for more advanced mathematical concepts. By mastering these basic ideas, you equip yourself with critical thinking skills and a powerful framework for problem-solving in numerous contexts. So, the next time you encounter a problem involving parts of a whole, remember the simplicity and power inherent in understanding "5 of 20."
Latest Posts
Latest Posts
-
Church Of The Nazarene Calgary
Sep 15, 2025
-
80 Oz Water To Liter
Sep 15, 2025
-
98 4 Degrees Fahrenheit To Celsius
Sep 15, 2025
-
Coat Of Arms Canada Meaning
Sep 15, 2025
-
Protons Neutrons Electrons Of Nitrogen
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.