What Is 75 Of 15
monicres
Sep 14, 2025 · 5 min read
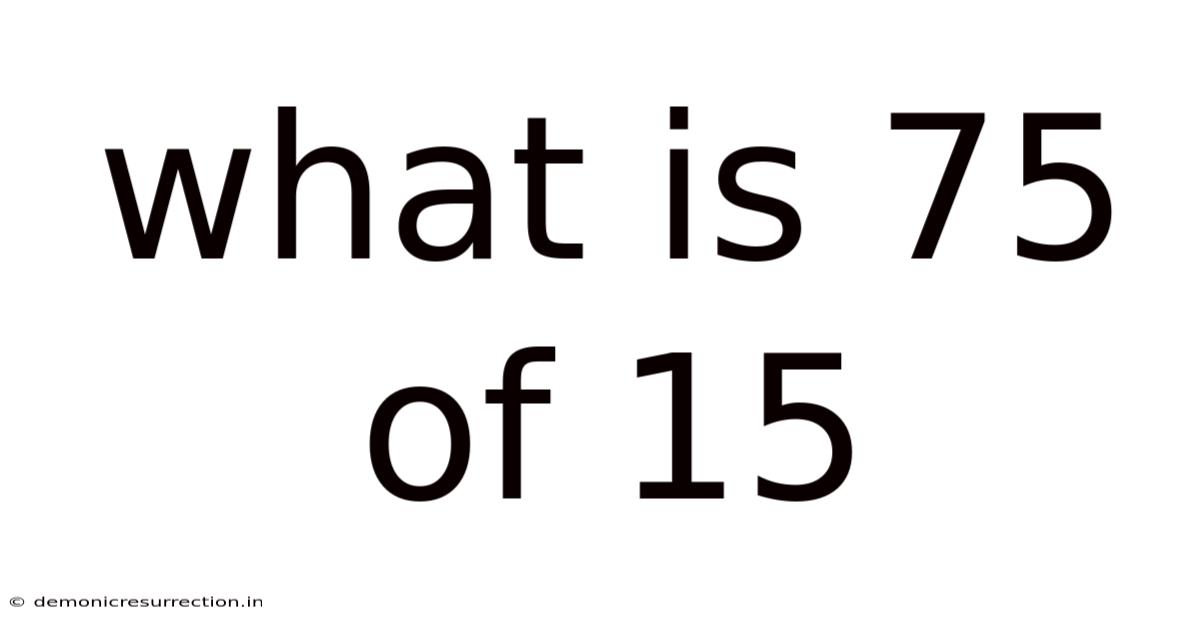
Table of Contents
What is 75% of 15? A Deep Dive into Percentages and Their Applications
Finding 75% of 15 might seem like a simple arithmetic problem, solvable with a quick calculation. However, understanding the underlying concepts of percentages and their diverse applications opens doors to a broader mathematical understanding and practical problem-solving skills. This article will not only solve the problem but also delve into the "why" behind the calculation, exploring various methods, real-world examples, and the significance of percentage calculations in different fields.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per centum" in Latin). Therefore, 75% means 75 out of 100, which can be written as the fraction 75/100 or the decimal 0.75. Understanding this fundamental concept is crucial to solving percentage problems.
Method 1: Using Fractions
The most straightforward method to calculate 75% of 15 involves converting the percentage to a fraction and then multiplying.
-
Convert the percentage to a fraction: 75% is equal to 75/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 25. This simplifies to 3/4.
-
Multiply the fraction by the number: Now, multiply the simplified fraction (3/4) by 15:
(3/4) * 15 = 45/4
-
Convert the improper fraction to a decimal or mixed number: 45/4 can be converted to a decimal by performing the division: 45 ÷ 4 = 11.25. Alternatively, it can be expressed as a mixed number: 11 ¼.
Therefore, 75% of 15 is 11.25.
Method 2: Using Decimals
Another common approach uses decimal representation of the percentage.
-
Convert the percentage to a decimal: 75% is equivalent to 0.75 (by dividing 75 by 100).
-
Multiply the decimal by the number: Multiply 0.75 by 15:
0.75 * 15 = 11.25
Again, we arrive at the answer: 75% of 15 is 11.25.
Method 3: Using Proportion
The concept of proportion provides a more visual and intuitive approach to solving percentage problems. A proportion sets up an equation relating two ratios.
-
Set up the proportion: We can set up a proportion as follows:
x/15 = 75/100
where 'x' represents the unknown value (75% of 15).
-
Solve for x: To solve for x, we can cross-multiply:
100x = 75 * 15 100x = 1125
-
Isolate x: Divide both sides by 100:
x = 1125/100 x = 11.25
Once again, the solution confirms that 75% of 15 is 11.25.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives, finding applications in various fields:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, if a store offers a 75% discount on an item priced at $15, the discount amount is 11.25, and the final price is $3.75.
-
Science: Percentage calculations are crucial in analyzing experimental data, expressing concentrations (e.g., 75% alcohol solution), and representing statistical results.
-
Retail: Calculating sales tax, discounts, and markups are all based on percentages. Understanding markups helps businesses determine profitable pricing strategies.
-
Education: Grading systems often use percentages to represent student performance. Calculating the percentage of correct answers on a test is a common practice.
-
Everyday Life: Determining tips in restaurants, calculating sale prices, and understanding nutritional information on food labels all involve percentages.
Understanding the Concept of "Of" in Percentage Problems
The word "of" in percentage problems signifies multiplication. When you see a phrase like "75% of 15," it means "75% multiplied by 15." This seemingly simple linguistic nuance is fundamental to correctly solving percentage problems.
Solving More Complex Percentage Problems
While the example of finding 75% of 15 is relatively straightforward, the same principles apply to more complex problems. For instance, calculating the percentage increase or decrease between two values, or finding a certain percentage of a larger number, involves the same core mathematical operations but might require additional steps. Mastering the fundamental methods outlined above provides a solid foundation for tackling these more complex scenarios.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a different percentage of 15?
A1: Simply replace 75% with the desired percentage and follow the same steps using any of the three methods described above (fraction, decimal, or proportion).
Q2: Can I use a calculator for these calculations?
A2: Absolutely! Calculators are valuable tools for performing these calculations quickly and accurately, especially for more complex percentage problems.
Q3: Are there any online tools or resources to help with percentage calculations?
A3: Yes, many online calculators and resources are available to help with percentage calculations. These tools can be particularly useful for complex problems or for verifying your calculations.
Q4: Why is understanding percentages important?
A4: Percentages are a fundamental part of many aspects of life, from finances to scientific analysis. Understanding them allows for better decision-making and comprehension of the world around us.
Q5: How can I improve my skills in calculating percentages?
A5: Consistent practice is key. Start with simple problems like the one discussed in this article and gradually work your way up to more complex scenarios. Using different methods to solve the same problem can also improve your understanding and problem-solving abilities.
Conclusion
Calculating 75% of 15, which equals 11.25, is a seemingly simple task. However, exploring the underlying principles of percentages, different calculation methods, and their wide-ranging applications offers a much richer understanding of this essential mathematical concept. From personal finance to scientific research, the ability to confidently work with percentages is a valuable skill applicable across numerous aspects of life. By mastering the techniques and understanding the applications discussed in this article, you'll be well-equipped to handle a broad spectrum of percentage-related problems with confidence and accuracy. Remember that consistent practice and a solid understanding of the underlying concepts are essential for developing proficiency in percentage calculations.
Latest Posts
Latest Posts
-
Weight Of Diesel Per Litre
Sep 14, 2025
-
Osprey Bird Vs Bald Eagle
Sep 14, 2025
-
1 60th Of A Dram
Sep 14, 2025
-
Torque Of A Motor Calculation
Sep 14, 2025
-
Into The Wild Book Synopsis
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.