What Times What Equals 36
monicres
Sep 20, 2025 · 6 min read
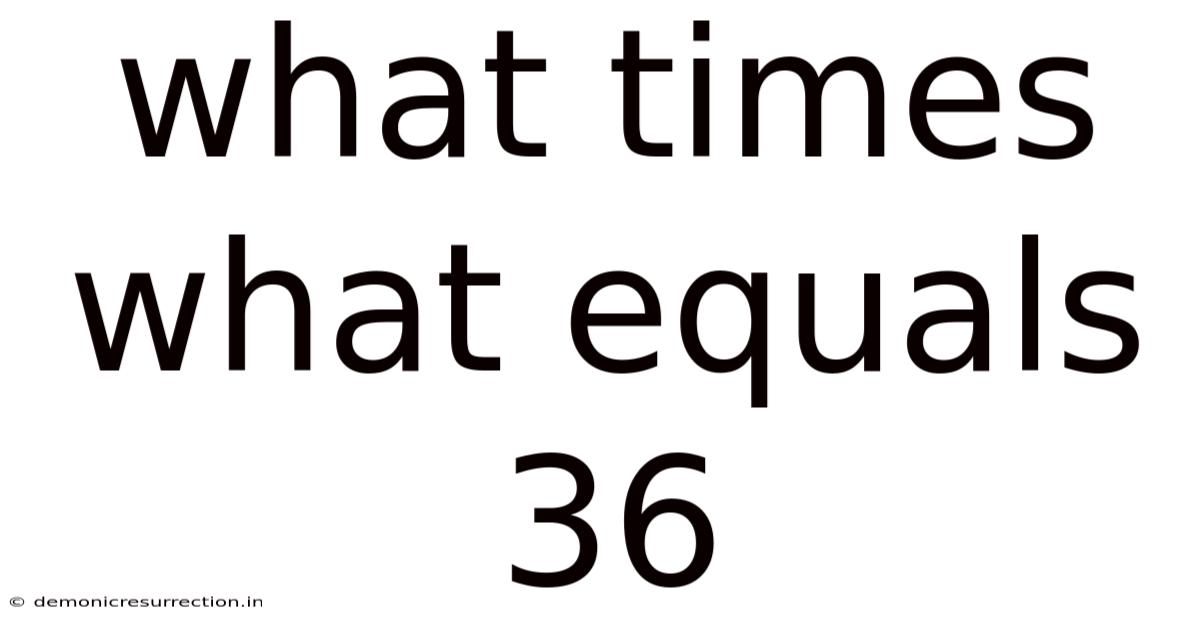
Table of Contents
What Times What Equals 36? Exploring the Factors and Applications of 36
Finding the numbers that, when multiplied, result in 36 might seem like a simple arithmetic problem. However, delving deeper reveals a fascinating exploration of factors, prime factorization, and the diverse applications of this seemingly humble number. This article will comprehensively examine all the possible pairs of numbers that multiply to 36, explore the concept of factors, delve into the prime factorization of 36, and discuss its relevance in various fields, from mathematics and geometry to real-world applications. Understanding the factors of 36 is fundamental to grasping more complex mathematical concepts.
Understanding Factors and Multiples
Before we dive into the specific factors of 36, let's clarify the basic mathematical concepts involved. A factor of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides evenly into 12. Conversely, a multiple of a number is the result of multiplying that number by any whole number. For example, multiples of 3 are 3, 6, 9, 12, 15, and so on.
Finding the factors of a number is a crucial step in many mathematical operations, including simplifying fractions, finding the greatest common factor (GCF), and understanding prime factorization.
All the Number Pairs that Equal 36
Now, let's tackle the central question: what times what equals 36? There are several pairs of numbers that, when multiplied, yield a product of 36. These pairs are:
- 1 x 36
- 2 x 18
- 3 x 12
- 4 x 9
- 6 x 6
These pairs represent all the whole number factors of 36. Note that the order of the numbers in each pair doesn't matter; 2 x 18 is the same as 18 x 2. This illustrates the commutative property of multiplication. If we consider negative numbers, we also have:
- -1 x -36
- -2 x -18
- -3 x -12
- -4 x -9
- -6 x -6
Prime Factorization of 36
Prime factorization is the process of expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. The prime factorization of 36 involves breaking it down into its prime components. We can do this using a factor tree:
36
/ \
6 6
/ \ / \
2 3 2 3
This shows that the prime factorization of 36 is 2 x 2 x 3 x 3, or 2² x 3². This representation is unique to 36; no other number has this exact prime factorization. Understanding prime factorization is vital in simplifying fractions, finding the least common multiple (LCM), and solving various algebraic problems.
Applications of 36 and its Factors in Various Fields
The number 36, and its factors, appear in various contexts, both in pure mathematics and in real-world applications:
1. Geometry:
-
Squares and Rectangles: The number 36 is particularly relevant in geometry. A square with sides of 6 units has an area of 36 square units (6 x 6). Rectangles with dimensions of 2 x 18, 3 x 12, and 4 x 9 also have an area of 36 square units. This showcases the multiple ways to represent the same area using different dimensions.
-
Degrees in a Circle: A circle has 360 degrees, and 36 is a factor of 360. This makes 36 a relevant unit in angular measurements.
2. Time:
- Hours in a Day: A day has 24 hours, and 36 is closely related (being a multiple of 12, which is half of 24). This connection helps in many time-related calculations and scheduling.
3. Number Systems:
- Base-6 System: Although less common than base-10, the number 36 plays a role in base-6 calculations as 6 x 6 = 36. It highlights the different ways we can represent quantities using diverse number systems.
4. Calendar:
- Days in Some Months: Some months have 30 days, and 36 (being a multiple of 6 and 12) provides a convenient reference point for estimations relating to dates and the length of time in months and years.
Real-World Examples
Beyond pure mathematics, the factors of 36 pop up in everyday situations:
-
Arranging Objects: Imagine you have 36 chocolates to arrange in a rectangular box. You could arrange them in multiple ways: 1 row of 36, 2 rows of 18, 3 rows of 12, 4 rows of 9, or 6 rows of 6. This demonstrates a practical application of finding the factors of a number.
-
Dividing Resources: If you have 36 liters of juice to distribute among several friends, the factors of 36 tell you the possible equal shares you can give out.
-
Construction and Design: In construction and design, architects and engineers often utilize factors of numbers, like 36, to determine dimensions and arrangements of spaces or materials.
Expanding the Scope: Beyond Whole Numbers
Our exploration so far has focused on whole numbers. However, the equation "what times what equals 36" can also be solved using fractions and decimals. For instance:
- 12 x 3 = 36
- 18 x 2 = 36
- 9 x 4 = 36
- 4.5 x 8 = 36
- 3 x 12 = 36
- 2 x 18 = 36
- 1.5 x 24 = 36
These examples illustrate that there are infinitely many pairs of numbers (including fractions and decimals) whose product is 36. The number of integer factor pairs, however, remains finite.
Frequently Asked Questions (FAQ)
Q: What is the greatest common factor (GCF) of 36 and other numbers?
A: The GCF depends on the other number. For example: * GCF(36, 24) = 12 * GCF(36, 18) = 18 * GCF(36, 15) = 3
Q: What is the least common multiple (LCM) of 36 and other numbers?
A: The LCM also depends on the other number. For example: * LCM(36, 24) = 72 * LCM(36, 18) = 36 * LCM(36, 15) = 180
Q: How many divisors does 36 have?
A: 36 has 9 divisors: 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Conclusion
The seemingly simple question, "What times what equals 36?" opens a gateway to a deeper understanding of fundamental mathematical concepts like factors, multiples, prime factorization, and their applications in various fields. From the geometry of squares to the practicalities of dividing resources, the number 36 and its factors play a significant, often overlooked, role in our everyday lives and in advanced mathematical calculations. This comprehensive exploration demonstrates that even the most basic arithmetic problems can hold surprising depth and relevance. By understanding the factors of 36, we gain valuable insights into the broader world of mathematics and its real-world applications.
Latest Posts
Latest Posts
-
Whats 30 Percent Of 600
Sep 20, 2025
-
How Do I Measure Humidity
Sep 20, 2025
-
Indirect Cash Flow Vs Direct
Sep 20, 2025
-
Symptoms Of Gluteus Medius Tear
Sep 20, 2025
-
125 Degrees F To C
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.