Whats 20 Percent Of 80
monicres
Sep 04, 2025 · 5 min read
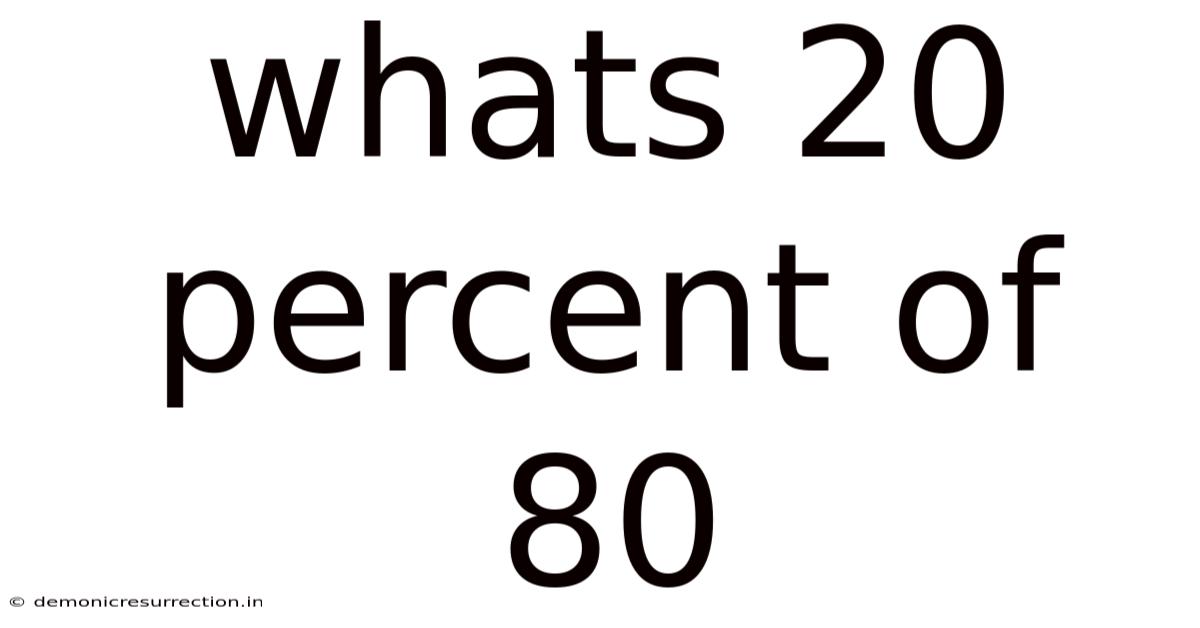
Table of Contents
What's 20 Percent of 80? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 80 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This article will not only answer the question directly but will also explore the underlying principles of percentages, different methods of calculation, and real-world examples to solidify your understanding. This comprehensive guide will equip you with the knowledge to tackle similar percentage problems with confidence.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. This fractional representation is crucial for understanding how to calculate percentages.
Calculating 20% of 80: Three Methods
There are several ways to calculate 20% of 80. Let's explore three common methods:
Method 1: Using the Fraction Method
As mentioned earlier, 20% is equivalent to 20/100, or 1/5. To find 20% of 80, we simply multiply 80 by the fraction 1/5:
80 x (1/5) = 16
Therefore, 20% of 80 is 16. This method is particularly useful for simple percentages that have easy-to-work-with fraction equivalents.
Method 2: Using Decimal Conversion
Percentages can be easily converted to decimals by dividing the percentage by 100. In this case, 20% becomes 20/100 = 0.20 or simply 0.2. To find 20% of 80, we multiply 80 by 0.2:
80 x 0.2 = 16
This method is generally preferred for its ease of use with calculators and its applicability to more complex percentages that don't have simple fraction equivalents.
Method 3: Using Proportions
This method uses the concept of ratios and proportions. We can set up a proportion to solve for the unknown value (x), which represents 20% of 80:
20/100 = x/80
To solve for x, we cross-multiply:
20 * 80 = 100 * x
1600 = 100x
x = 1600/100
x = 16
This method highlights the relationship between the percentage, the whole, and the part. It is a more formal approach and beneficial for understanding the underlying mathematical principles.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-world scenarios. Here are some examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. If a $80 item is on sale for 20% off, you'll save $16 (20% of 80), making the final price $64.
-
Taxes and Tips: Calculating sales tax or a restaurant tip involves percentages. If the sales tax is 6%, you would calculate 6% of the total price to determine the additional tax. Similarly, a 15% tip on an $80 meal would amount to $12 (15% of 80).
-
Financial Analysis: Percentages are vital in understanding financial statements. Analyzing profit margins, return on investment (ROI), and growth rates all rely heavily on percentage calculations. For example, a company might report a 20% increase in revenue, which means its revenue grew by 20% of its previous year’s revenue.
-
Statistics and Probability: Percentages are frequently used to represent data in statistical analyses and probability calculations. For instance, researchers might report that 20% of participants in a study showed a particular outcome.
-
Grade Calculation: Many grading systems use percentages. If a test is worth 20% of your final grade, and you score 80% on the test, it contributes 16% (20% of 80%) towards your final grade.
-
Compound Interest: Understanding compound interest, crucial for saving and investing, involves repeated percentage calculations. The interest earned in one period is added to the principal, and the interest for the next period is calculated on the new, larger principal.
-
Surveys and Polls: Results of surveys and polls are often presented using percentages to represent the proportion of respondents who selected a particular answer.
Beyond the Basics: More Complex Percentage Problems
While calculating 20% of 80 is straightforward, understanding the principles allows you to tackle more complex problems. For example:
- Finding the original amount: If an item is on sale for $64 after a 20% discount, you can use algebra to find the original price:
Let x be the original price. Then, x - 0.2x = 64. Solving for x, we get x = 80.
- Calculating percentage increase or decrease: If a value increases from 80 to 100, the percentage increase is calculated as [(100-80)/80] x 100% = 25%.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on the specific percentage and your comfort level. Using decimal conversion (dividing the percentage by 100 and multiplying) is generally straightforward and works well with a calculator for any percentage.
Q: How can I calculate percentages without a calculator?
A: For simple percentages like 10%, 25%, and 50%, you can use mental math and fraction equivalents. For more complex percentages, you can use the proportion method and long division.
Q: What are some common percentage mistakes to avoid?
A: Common mistakes include confusing percentage increase and decrease calculations, misplacing decimal points when converting percentages to decimals, and incorrectly setting up proportions. Carefully reviewing your steps and using a calculator for complex calculations can minimize errors.
Q: Are there online tools to calculate percentages?
A: Yes, many online calculators and websites are available to quickly and accurately compute percentage calculations. However, understanding the underlying principles is crucial for problem-solving and avoiding dependence on external tools.
Conclusion
Calculating 20% of 80, resulting in 16, is a simple yet foundational calculation that illustrates the broader application of percentages in various aspects of life. Mastering percentage calculations not only aids in solving everyday problems but also strengthens mathematical skills and enhances problem-solving abilities across diverse fields. Understanding the different methods—using fractions, decimals, and proportions—provides flexibility and a deeper understanding of the concept. By applying this knowledge, you'll be better equipped to handle percentage-related challenges with confidence and efficiency. Remember to practice regularly to solidify your understanding and become proficient in this essential mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.