Whats 25 Percent Of 200
monicres
Sep 17, 2025 · 6 min read
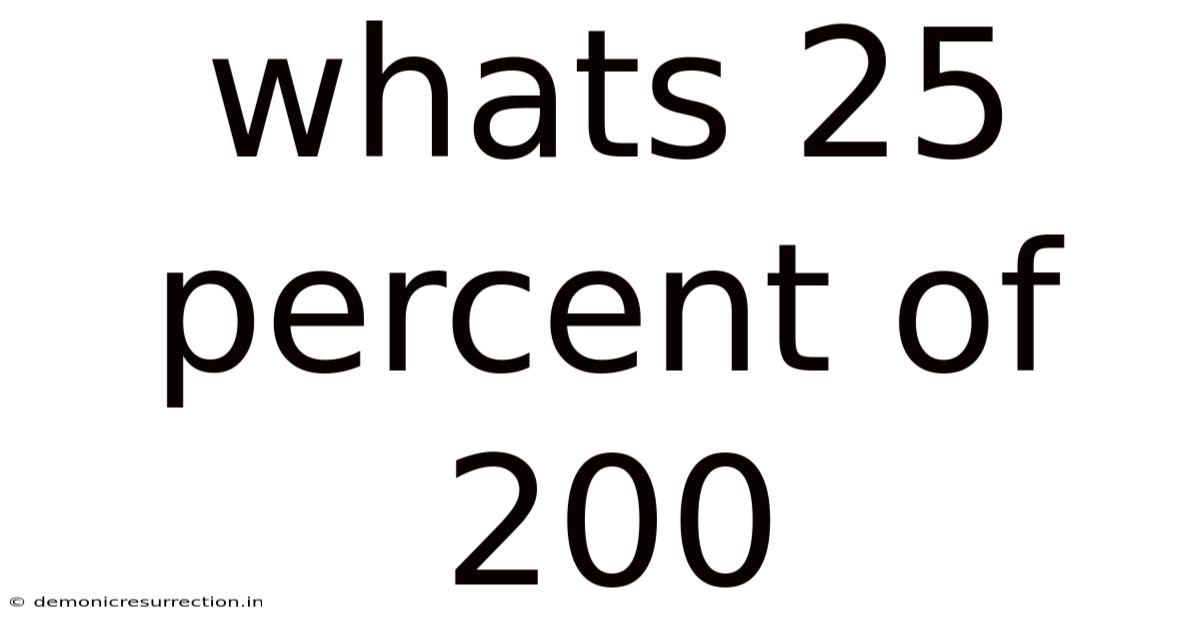
Table of Contents
What's 25 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 200 might seem like a simple calculation, easily solvable with a calculator. However, understanding the underlying principles of percentages and their broad applications in various fields is crucial for everyday life, academic pursuits, and professional success. This article will not only answer the question "What's 25 percent of 200?" but will also delve into the core concepts of percentages, explore different methods of calculation, and showcase their relevance in real-world scenarios.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Essentially, a percentage expresses a proportion of a whole. For instance, 50% represents 50 out of 100, or one-half (1/2). Understanding this fundamental concept is key to comprehending percentage calculations.
Method 1: The Basic Calculation – Fraction Method
The most straightforward method to calculate 25% of 200 involves converting the percentage to a fraction and then multiplying it by the number.
-
Step 1: Convert the percentage to a fraction: 25% can be expressed as 25/100. This fraction can be simplified to 1/4.
-
Step 2: Multiply the fraction by the number: (1/4) * 200 = 50
Therefore, 25% of 200 is 50.
Method 2: The Decimal Method
Another common approach uses decimals. Percentages can easily be converted to decimals by dividing the percentage by 100.
-
Step 1: Convert the percentage to a decimal: 25% / 100 = 0.25
-
Step 2: Multiply the decimal by the number: 0.25 * 200 = 50
Again, the answer remains 50.
Method 3: Using Proportions
This method utilizes the concept of proportions, offering a more versatile approach applicable to various percentage problems.
-
Set up a proportion: We can represent the problem as a ratio: x/200 = 25/100, where 'x' represents the unknown value (25% of 200).
-
Cross-multiply: 100x = 25 * 200
-
Solve for x: 100x = 5000 => x = 5000/100 => x = 50
Once more, we arrive at the answer: 50.
Why is Understanding Percentages Important?
The ability to calculate percentages is a fundamental skill applicable across a vast range of contexts:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage changes allows for analyzing market trends and making informed financial decisions. For example, calculating a 15% discount on a $200 item involves finding 15% of $200, which is crucial for determining the final price.
-
Science and Statistics: Percentages are essential in representing data, calculating probabilities, and analyzing statistical trends. Scientific reports often express results as percentages, enabling comparisons and interpretations of experimental findings. For instance, expressing the success rate of a treatment as a percentage helps in assessing its effectiveness.
-
Everyday Life: From calculating tips in restaurants (e.g., a 15% tip on a $50 bill) to understanding sales promotions (e.g., a 20% off sale), percentages are an integral part of our daily lives. Even determining the percentage of a specific ingredient in a recipe uses this mathematical concept.
-
Education: A solid understanding of percentages is crucial for success in mathematics, science, and other quantitative subjects. It's a building block for more advanced mathematical concepts. Calculating grades, test scores, and evaluating progress often involves working with percentages.
Practical Applications and Real-World Examples
Let's explore how percentage calculations are relevant in diverse real-world scenarios:
-
Sales and Discounts: A store offers a 25% discount on an item priced at $200. The discount amount is 25% of $200, which is $50. The final price after the discount is $200 - $50 = $150.
-
Taxes: If the sales tax in a region is 6%, and you buy an item costing $200, the tax amount is 6% of $200, which is $12. The total cost, including tax, is $200 + $12 = $212.
-
Interest Calculations: Suppose you deposit $200 in a savings account with an annual interest rate of 5%. After one year, the interest earned will be 5% of $200, which is $10.
-
Surveys and Polls: Survey results often present data as percentages. For instance, if 60% of respondents in a survey favor a particular policy, it indicates that 60 out of every 100 respondents hold that preference.
-
Grade Calculation: If a test is worth 200 points, and a student scores 150 points, their percentage score would be (150/200) * 100% = 75%.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond basic percentage calculations, understanding percentage increases and decreases is crucial for interpreting data and making informed decisions.
-
Percentage Increase: This calculates the increase in a value relative to the original value, expressed as a percentage. The formula is: [(New Value - Original Value) / Original Value] * 100%
-
Percentage Decrease: This calculates the decrease in a value relative to the original value, expressed as a percentage. The formula is: [(Original Value - New Value) / Original Value] * 100%
For instance, if a stock price increases from $100 to $125, the percentage increase is [(125 - 100) / 100] * 100% = 25%. Conversely, if the price drops from $125 to $100, the percentage decrease is [(125 - 100) / 125] * 100% = 20%.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate a percentage of a number without a calculator?
A: You can use the fraction method or the decimal method, as described above. For simpler percentages like 25%, 50%, 75%, or 10%, converting to fractions often makes manual calculation easier.
-
Q: What if I need to find a percentage of a number that is not a whole number?
A: The methods described above work equally well for numbers with decimals. Simply perform the calculation as usual.
-
Q: How can I reverse a percentage calculation? For example, if I know 25% of a number is 50, how do I find the original number?
A: Divide the known value by the percentage (expressed as a decimal). In this case, 50 / 0.25 = 200.
-
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, numerous online percentage calculators are available. These tools can simplify calculations and save time.
Conclusion: Mastering Percentages for a Brighter Future
Mastering percentage calculations is more than just learning a mathematical skill; it's acquiring a valuable tool applicable in various aspects of life. From managing personal finances and interpreting scientific data to making informed decisions in everyday scenarios, a solid understanding of percentages equips you with the knowledge to navigate the complexities of the modern world more effectively. This article has demonstrated the fundamental concepts, different calculation methods, and showcased the broad applicability of percentages, enabling you to confidently tackle percentage-related problems and excel in various academic and professional endeavors. Remember that practice is key to mastering any skill; the more you apply these methods, the more comfortable and proficient you'll become in handling percentages.
Latest Posts
Latest Posts
-
What Is A Employer Name
Sep 17, 2025
-
Examples Of Tone In Poetry
Sep 17, 2025
-
Ruler In Mm Actual Size
Sep 17, 2025
-
The Love Of Good Woman
Sep 17, 2025
-
Bohr Rutherford Diagram For Potassium
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.