Whats 40 Percent Of 60
monicres
Sep 17, 2025 · 5 min read
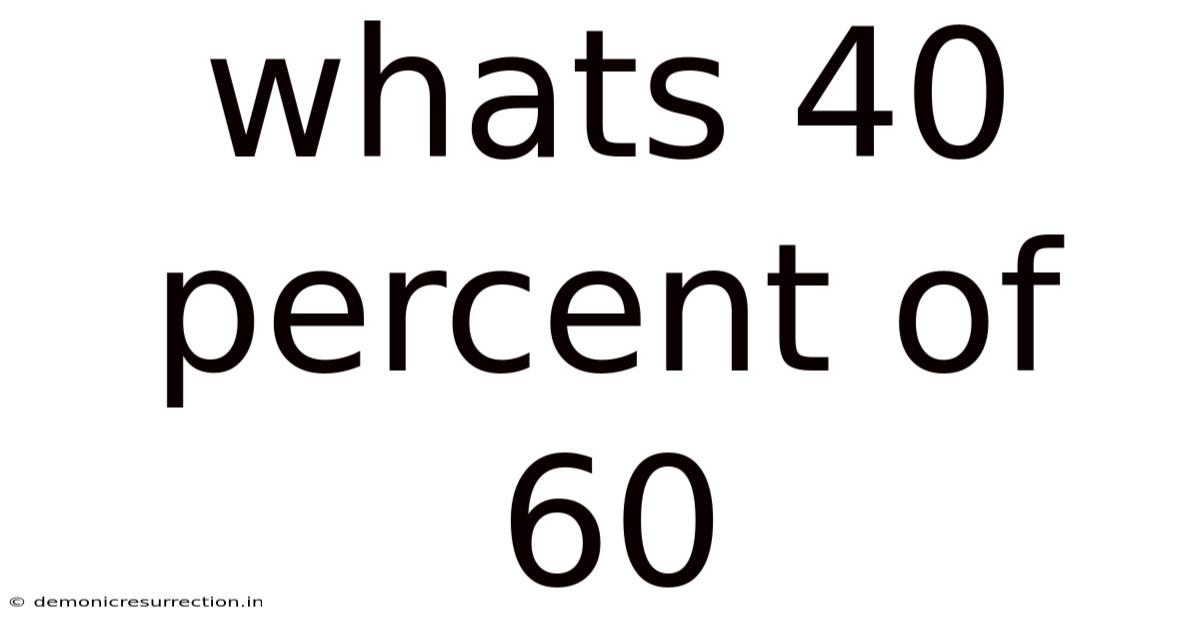
Table of Contents
What's 40 Percent of 60? A Deep Dive into Percentages and Their Applications
Finding 40 percent of 60 might seem like a simple calculation, but it opens a door to understanding a fundamental concept in mathematics and its widespread applications in everyday life. This article will not only answer the question directly but also explore the underlying principles of percentages, different methods for calculating them, and real-world examples demonstrating their importance. We'll delve into the theoretical basis, practical techniques, and even touch upon more advanced percentage-related problems. By the end, you'll have a solid grasp of percentages and be confident in tackling similar calculations.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 40 percent (40%) means 40 out of 100, or 40/100. This fraction can be simplified to 2/5. Understanding this fundamental relationship is key to solving percentage problems.
Method 1: The Fraction Method
This method directly applies the definition of a percentage. To find 40% of 60, we first convert 40% into a fraction:
40% = 40/100 = 2/5
Next, we multiply this fraction by 60:
(2/5) * 60 = 120/5 = 24
Therefore, 40% of 60 is 24.
Method 2: The Decimal Method
This method involves converting the percentage into a decimal. To do this, we divide the percentage by 100:
40% ÷ 100 = 0.40 or simply 0.4
Then, we multiply this decimal by 60:
0.4 * 60 = 24
Again, we find that 40% of 60 is 24.
Method 3: Using Proportions
This method uses the concept of ratios and proportions. We can set up a proportion:
x / 60 = 40 / 100
Where 'x' represents the unknown value (40% of 60). To solve for x, we cross-multiply:
100x = 40 * 60
100x = 2400
x = 2400 / 100
x = 24
So, 40% of 60 is 24. This method is particularly useful when dealing with more complex percentage problems.
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives. Here are just a few examples:
- Sales and Discounts: Stores frequently advertise discounts like "40% off." Understanding percentages allows you to quickly calculate the final price after the discount.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount requires understanding percentage calculations.
- Interest Rates: Interest rates on loans, savings accounts, and credit cards are expressed as percentages. Knowing how to calculate interest is crucial for financial planning.
- Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. Graphs and charts frequently use percentages to represent proportions and trends.
- Tip Calculations: When dining out, calculating a tip (e.g., 15% or 20%) requires understanding percentage calculations.
- Grade Calculation: In education, your final grade is often calculated based on the percentage of correct answers on tests and assignments.
Beyond the Basics: More Complex Percentage Problems
While finding 40% of 60 is relatively straightforward, let's explore more challenging percentage problems to further solidify your understanding:
Scenario 1: Finding the Original Amount
Let's say you bought an item on sale for $24 after a 40% discount. How much did the item originally cost?
In this case, we know that $24 represents 60% of the original price (100% - 40% = 60%). We can set up a proportion:
24 / x = 60 / 100
Cross-multiplying and solving for x (the original price), we get:
60x = 2400
x = 40
The original price of the item was $40.
Scenario 2: Calculating Percentage Increase or Decrease
Suppose your salary increased from $60,000 to $72,000. What is the percentage increase?
First, calculate the difference: $72,000 - $60,000 = $12,000
Then, divide the difference by the original salary and multiply by 100%:
($12,000 / $60,000) * 100% = 20%
Your salary increased by 20%.
Scenario 3: Compound Interest
Compound interest is interest calculated on both the principal amount and accumulated interest from previous periods. Understanding compound interest is crucial for long-term financial planning. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
For example, if you invest $1000 at an annual interest rate of 5% compounded annually for 3 years, the calculation would be:
A = 1000 (1 + 0.05/1)^(1*3) = $1157.63
Frequently Asked Questions (FAQ)
- Q: What is the easiest way to calculate percentages?
A: The decimal method is often the easiest and quickest for simple calculations. Converting the percentage to a decimal and multiplying by the number is straightforward.
- Q: How do I calculate percentages without a calculator?
A: You can use the fraction method, which relies on basic arithmetic. However, for more complex calculations, a calculator is recommended for accuracy and efficiency.
- Q: What if the percentage is greater than 100%?
A: A percentage greater than 100% means the result is larger than the original number. For example, 150% of 60 is (1.5 * 60) = 90. This often represents growth or increase beyond the original value.
- Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many websites and apps offer free percentage calculators that can help you with various percentage-related calculations.
Conclusion: Mastering Percentages
This article has demonstrated that finding 40% of 60, while seemingly simple, provides a gateway to understanding the broader concept of percentages and their critical role in numerous aspects of life. Whether you're calculating discounts, interest, taxes, or analyzing data, a solid grasp of percentage calculations is an invaluable skill. By mastering the different methods presented – the fraction method, decimal method, and proportion method – and exploring the examples provided, you can confidently tackle various percentage problems and apply this knowledge to your everyday life. Remember that practice is key; the more you work with percentages, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
Best Names For A Duck
Sep 17, 2025
-
Salary Of A Catholic Cardinal
Sep 17, 2025
-
What Is 25 Of 50
Sep 17, 2025
-
Linear And Non Linear Thinking
Sep 17, 2025
-
What Is Capital Of Madagascar
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Whats 40 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.