X 3 X 4 8
monicres
Sep 12, 2025 · 6 min read
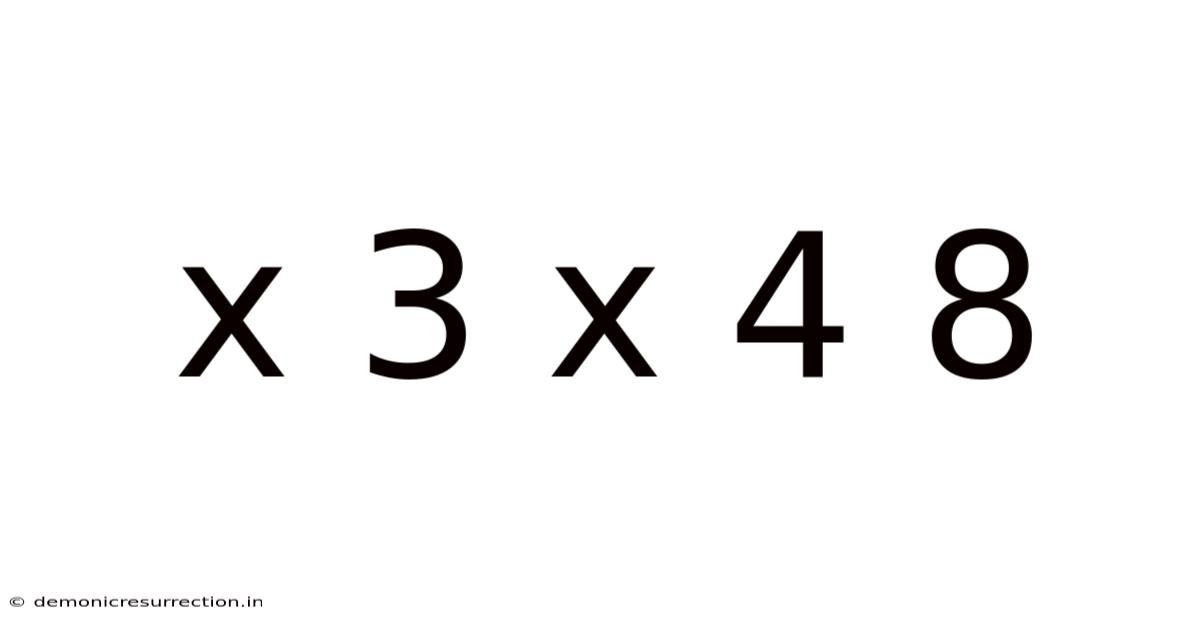
Table of Contents
Decoding the Mystery: Exploring the Mathematical Relationship of "x 3 x 4 = 8"
This article delves into the seemingly simple equation "x 3 x 4 = 8," exploring its various interpretations, potential solutions, and the underlying mathematical principles involved. While the equation, as presented, might seem incomplete or even incorrect, it opens a fascinating gateway to understanding algebraic manipulation, order of operations, and the importance of precise notation in mathematics. This exploration will be beneficial for anyone interested in strengthening their foundational mathematical skills.
Introduction: Unveiling the Ambiguity
At first glance, the equation "x 3 x 4 = 8" appears straightforward. However, its lack of explicit operators (like "+" or "-") and the potential ambiguity in interpretation necessitate a more in-depth analysis. The equation can be interpreted in several ways, leading to different solutions and highlighting the critical role of clear mathematical notation. This exploration will cover various interpretations and systematically solve them, emphasizing the order of operations (PEMDAS/BODMAS) and algebraic techniques.
Possible Interpretations and Solutions
The ambiguity stems from the lack of clearly defined operators between the variables and numbers. We can interpret the equation in several ways, each requiring a unique approach to solving for 'x':
1. Interpretation 1: Implicit Multiplication
If we assume that the equation represents implicit multiplication, it can be rewritten as:
x * 3 * 4 = 8
This is a simple algebraic equation. To solve for 'x', we perform the following steps:
- Combine constants: 3 * 4 = 12
- Rewrite the equation: 12x = 8
- Isolate 'x': x = 8/12
- Simplify: x = 2/3
Therefore, under this interpretation, the solution is x = 2/3.
2. Interpretation 2: Mixed Operations (Possible Scenarios)
The equation might represent a mixture of addition, subtraction, multiplication, or division. Let's explore some possibilities:
-
Scenario A: (x + 3) x 4 = 8
- Divide both sides by 4: x + 3 = 2
- Subtract 3 from both sides: x = -1
-
Scenario B: x + (3 x 4) = 8
- Simplify the parentheses: x + 12 = 8
- Subtract 12 from both sides: x = -4
-
Scenario C: (x x 3) + 4 = 8
- Subtract 4 from both sides: 3x = 4
- Divide both sides by 3: x = 4/3
-
Scenario D: x x (3 + 4) = 8
- Simplify the parentheses: 7x = 8
- Divide both sides by 7: x = 8/7
These scenarios demonstrate how crucial clear notation is. Without parentheses or explicit operators, the equation is highly susceptible to multiple interpretations, each yielding a different solution. This highlights the importance of precision in mathematical expressions.
3. Interpretation 3: Considering Exponents
While less likely without explicit notation, we could hypothetically interpret the equation involving exponents:
-
Scenario E: x³ x 4 = 8
- Divide both sides by 4: x³ = 2
- Take the cube root of both sides: x = ∛2 (approximately 1.26)
-
Scenario F: x x 3⁴ = 8
- Simplify the exponent: x x 81 = 8
- Divide both sides by 81: x = 8/81
These scenarios, involving exponents, further illustrate the ambiguity inherent in the original, poorly defined equation. The solution is heavily dependent on the assumed operations.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), is crucial in evaluating mathematical expressions. It dictates the sequence in which operations should be performed to obtain the correct result.
The original equation "x 3 x 4 = 8" lacks the clarity to definitively apply PEMDAS/BODMAS. The presence or absence of parentheses drastically alters the solution. This emphasizes the need for precise mathematical notation to avoid ambiguity and ensure that the intended operations are correctly interpreted.
For example, if the equation were written as (x * 3) * 4 = 8, the order of operations is clear, leading to the solution x = 2/3 (as shown in Interpretation 1). However, if written as x * (3 * 4) = 8, the solution would still be x = 2/3. The placement of parentheses significantly impacts the order of calculations.
Algebraic Manipulation Techniques
Solving algebraic equations, such as those derived from interpreting "x 3 x 4 = 8," involves using various techniques to isolate the unknown variable ('x'). These techniques include:
- Addition/Subtraction Property of Equality: Adding or subtracting the same value from both sides of an equation maintains the equality.
- Multiplication/Division Property of Equality: Multiplying or dividing both sides of an equation by the same non-zero value maintains the equality.
- Distributive Property: This property allows us to expand expressions like a(b + c) = ab + ac.
- Combining like terms: Simplifying expressions by adding or subtracting terms with the same variable and exponent.
Mastering these algebraic manipulation techniques is essential for solving a wide range of mathematical problems, including those involving more complex equations than the one under consideration.
The Role of Precise Mathematical Notation
This exercise with "x 3 x 4 = 8" powerfully demonstrates the critical importance of precise mathematical notation. Ambiguity in notation leads to multiple interpretations and potentially incorrect solutions. Using parentheses to clearly group operations, employing explicit operators (+, -, *, /), and using proper formatting are crucial for clear communication in mathematics.
The use of appropriate symbols and clear structuring of the equation avoids any misunderstanding and ensures the correct application of the order of operations. This is paramount not only for solving simple equations but also for tackling more complex mathematical problems and ensuring accurate communication in any field involving mathematics.
Frequently Asked Questions (FAQ)
Q: Is there a single correct answer to "x 3 x 4 = 8"?
A: No, without explicit operators or parentheses, there is no single correct answer. The equation is inherently ambiguous, leading to multiple valid solutions depending on the interpretation of the implied operations.
Q: Why is it important to use parentheses in mathematical equations?
A: Parentheses dictate the order of operations, ensuring that calculations are performed correctly. They eliminate ambiguity and ensure a single, unambiguous solution.
Q: What are some common mistakes students make when solving algebraic equations?
A: Common mistakes include incorrectly applying the order of operations, making errors in algebraic manipulation (e.g., incorrectly adding or subtracting terms), and neglecting to check solutions for validity.
Q: How can I improve my skills in solving algebraic equations?
A: Consistent practice, understanding the fundamental principles of algebra (e.g., properties of equality), and working through a variety of problem types are crucial for improvement. Seeking help from teachers or tutors when needed can significantly aid understanding.
Conclusion: Lessons Learned from Ambiguity
The seemingly simple equation "x 3 x 4 = 8" serves as a valuable lesson in the importance of precise mathematical notation and the application of the order of operations. The ambiguity inherent in the equation highlights the critical need for clear communication in mathematics. Understanding different interpretations and solutions allows us to appreciate the nuances of algebraic manipulation and strengthens our foundational mathematical skills. This analysis should reinforce the importance of clear communication and rigorous attention to detail when working with any mathematical expression. The exercise emphasizes that proper notation is not merely a stylistic choice but a fundamental requirement for accurate and unambiguous mathematical expression and problem-solving.
Latest Posts
Latest Posts
-
Lenina Crowne Brave New World
Sep 12, 2025
-
Night Of The Museum Sacagawea
Sep 12, 2025
-
Going To Be In Spanish
Sep 12, 2025
-
Ln 1 X Taylor Series
Sep 12, 2025
-
What Is 10 Of 2000
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.