X Square Root Of X
monicres
Sep 17, 2025 · 7 min read
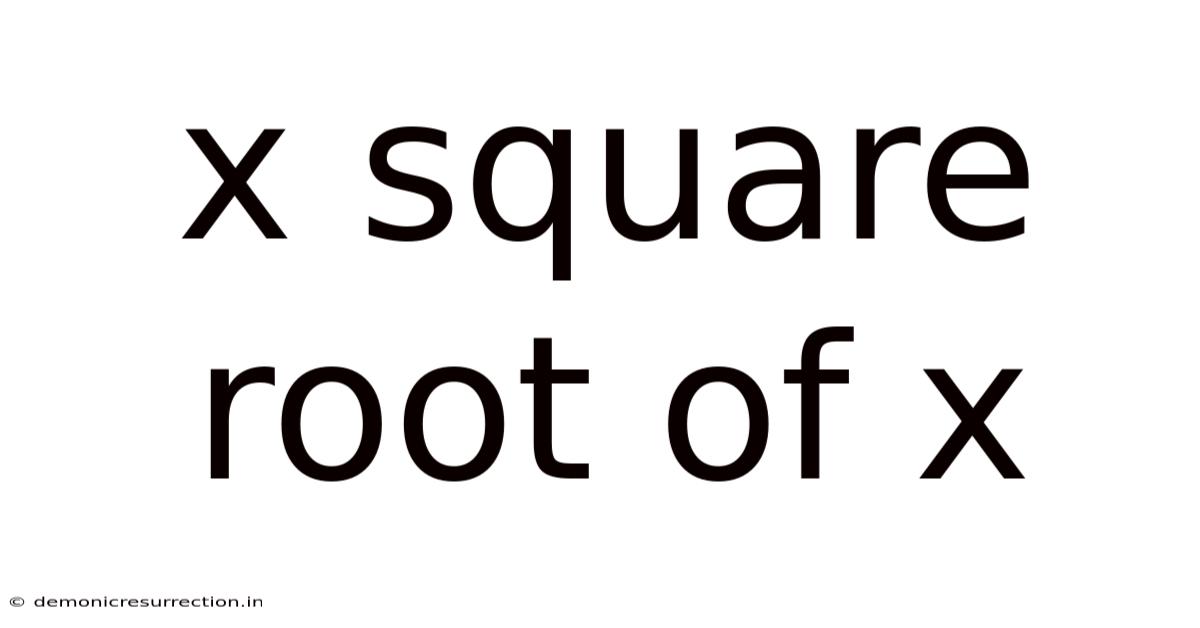
Table of Contents
Decoding x√x: A Deep Dive into the Mathematics of Exponential and Radical Expressions
Understanding the mathematical expression x√x might seem daunting at first glance, but with a structured approach, we can break it down into manageable components and appreciate its significance in various mathematical applications. This article provides a comprehensive exploration of x√x, covering its simplification, graphical representation, applications, and common misconceptions. This will equip you with a strong foundational understanding of this seemingly complex expression.
Introduction: Unveiling the Mystery of x√x
The expression x√x, often encountered in algebra and calculus, represents the product of a variable x and its square root. While it might appear simple at first, it encapsulates important concepts in exponents and radicals, highlighting the interconnectedness of different mathematical operations. Understanding this expression unlocks a deeper appreciation for manipulating algebraic expressions and solving complex equations. This article aims to demystify x√x, guiding you through its simplification, graphical interpretation, practical applications, and addressing frequently asked questions. By the end, you will not only be able to simplify this expression but also understand its broader mathematical implications.
1. Simplifying x√x: Harnessing the Power of Exponents
The key to simplifying x√x lies in understanding the relationship between radicals and exponents. Recall that the square root of a number, √x, is equivalent to x^(1/2). Therefore, we can rewrite x√x as:
x * x^(1/2)
Using the rules of exponents, specifically the rule for multiplying terms with the same base (a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>), we can simplify further:
x<sup>1</sup> * x<sup>1/2</sup> = x<sup>(1 + 1/2)</sup> = x<sup>3/2</sup>
Therefore, x√x simplifies to x<sup>3/2</sup>. This fractional exponent representation is often more useful in calculus and other advanced mathematical contexts. This simple manipulation reveals the elegant connection between seemingly disparate mathematical concepts.
2. Graphical Representation: Visualizing the Behavior of x<sup>3/2</sup>
Visualizing the function y = x<sup>3/2</sup> provides valuable insights into its behavior. The graph of this function shows several key characteristics:
-
Domain and Range: The domain of the function is x ≥ 0, as we cannot take the square root of a negative number. The range is also y ≥ 0, reflecting the non-negative nature of the function's output.
-
Shape: The graph starts at the origin (0,0) and increases steadily as x increases. The rate of increase accelerates as x grows larger, indicating a non-linear relationship. The curve is smooth and continuous within its domain.
-
Intercept: The only intercept is at the origin (0,0).
Understanding the graphical representation helps visualize how the value of x√x changes with different values of x. This visual interpretation is invaluable for understanding the function's behavior and applications.
3. Applications of x<sup>3/2</sup>: Real-World Connections
While x√x might seem like an abstract mathematical concept, it finds applications in several areas, including:
-
Physics: The expression can appear in formulas related to various physical phenomena involving power laws and relationships between quantities. For example, certain types of wave propagation or energy dissipation problems might involve such terms.
-
Engineering: Similar to physics, engineering applications often involve power laws and relationships that lead to expressions like x<sup>3/2</sup>.
-
Calculus: In calculus, this expression frequently appears during integration and differentiation problems, particularly when dealing with power functions and their derivatives. Mastering its simplification is crucial for efficient problem-solving in these contexts.
-
Economics and Finance: While less direct, fractional power functions, including x<sup>3/2</sup>, sometimes show up in models describing economic growth or the behavior of financial markets under certain conditions.
These are just a few examples; the applicability of x<sup>3/2</sup> extends to various scientific and engineering fields.
4. Exploring Related Concepts: Expanding Your Mathematical Toolkit
Understanding x√x provides a springboard to explore related concepts in mathematics, such as:
-
Fractional Exponents: The simplification of x√x heavily relies on the understanding of fractional exponents and their relationship to radicals. Mastering this fundamental concept is essential for advanced mathematical studies.
-
Radical Expressions: The initial expression involves a radical, emphasizing the importance of understanding how to manipulate and simplify radical expressions efficiently.
-
Power Rules of Exponents: Applying the rules of exponents, particularly the power rule for multiplication, is crucial in simplifying the expression.
-
Function Analysis: Graphing and analyzing the function y = x<sup>3/2</sup> involves understanding key characteristics like domain, range, intercepts, and behavior.
By exploring these interconnected concepts, you build a comprehensive mathematical foundation that will serve you well in future studies.
5. Addressing Common Misconceptions: Avoiding Pitfalls
Several common misconceptions can arise when dealing with expressions like x√x:
-
Incorrect Simplification: Some might mistakenly try to simplify x√x as √(x²), which is incorrect. Remember, x√x = x * x^(1/2) and not (x*x)^(1/2).
-
Neglecting the Domain: It's crucial to remember that the square root is only defined for non-negative numbers. Therefore, the domain of x√x and x<sup>3/2</sup> is x ≥ 0.
-
Confusing with other functions: Don't confuse x√x with similar-looking functions such as x²√x or √(x³). Each function has distinct properties and simplifications.
By avoiding these common mistakes, you can ensure accurate calculations and a deeper understanding of the expression.
6. Frequently Asked Questions (FAQ): Clarifying Common Doubts
Q: Can x be negative in the expression x√x?
A: No, x cannot be negative because the square root of a negative number is not a real number. The domain of the function is restricted to x ≥ 0.
Q: What is the derivative of x√x?
A: Using the power rule of differentiation, the derivative of x<sup>3/2</sup> is (3/2)x<sup>1/2</sup>, or (3/2)√x.
Q: How do I solve an equation involving x√x?
A: Solving an equation involving x√x usually requires isolating the term x√x and then simplifying using the exponential form x<sup>3/2</sup>. You may need to use algebraic manipulation techniques depending on the context of the equation. Sometimes, numerical methods might be necessary for complex equations.
Q: What is the integral of x√x?
A: The indefinite integral of x<sup>3/2</sup> is (2/5)x<sup>5/2</sup> + C, where C is the constant of integration.
Q: Are there any other ways to represent x√x?
A: While x<sup>3/2</sup> is the most concise and commonly used representation, you can also represent it as (x<sup>3</sup>)<sup>1/2</sup> or √(x³), although x<sup>3/2</sup> is generally preferred for its simplicity and applicability in calculus.
7. Conclusion: Mastering the Fundamentals of x√x
This in-depth exploration of x√x has demonstrated that, despite its seemingly simple appearance, this expression encompasses significant mathematical concepts. By understanding its simplification, graphical representation, applications, and common misconceptions, you have gained a solid understanding of its role within a broader mathematical framework. Remember, the journey of mastering mathematics is built upon understanding fundamental concepts like this one, laying a strong foundation for future explorations into more advanced topics. The ability to manipulate and interpret x√x, or its equivalent x<sup>3/2</sup>, is not merely an exercise in algebraic manipulation, but a crucial step in expanding your mathematical prowess and unlocking your potential in various scientific and technical fields. The key takeaway is that a methodical approach, coupled with a solid grasp of fundamental mathematical principles, empowers you to tackle seemingly complex expressions and unlock their hidden elegance and applications.
Latest Posts
Latest Posts
-
Tallest Mountain On Each Continent
Sep 17, 2025
-
What Is A Card Stock
Sep 17, 2025
-
Chinese Cinderella Adeline Yen Mah
Sep 17, 2025
-
Flags Of Spanish Speaking Countries
Sep 17, 2025
-
Normal Line Vs Tangent Line
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about X Square Root Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.