X X 1 X 2
monicres
Sep 16, 2025 · 6 min read
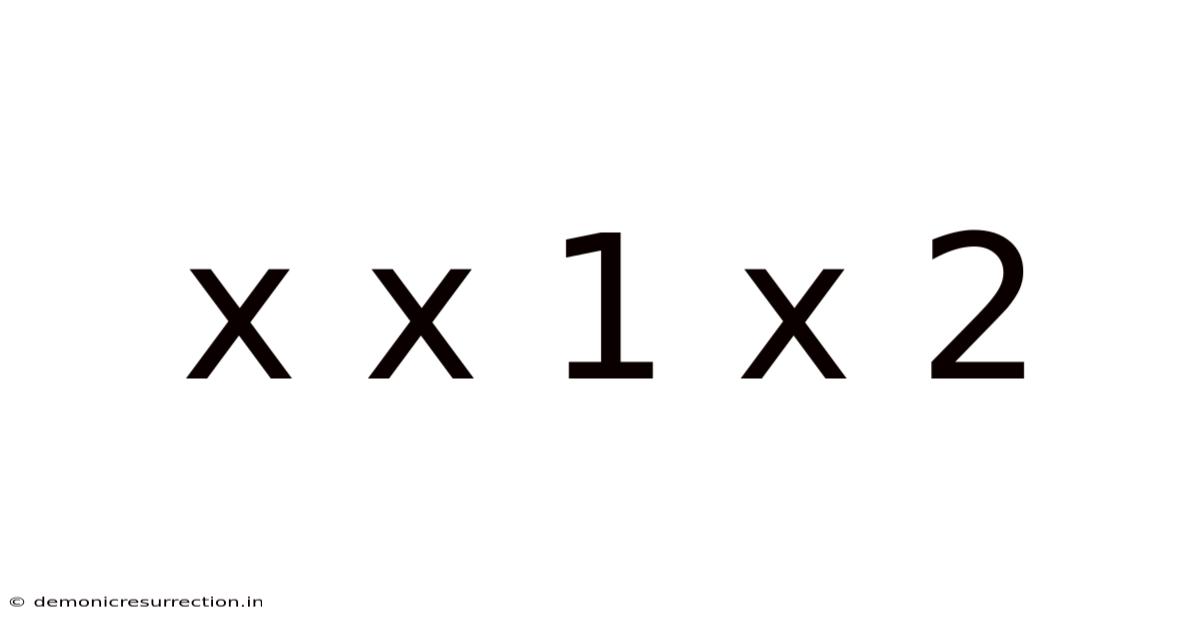
Table of Contents
Decoding the Mystery: A Deep Dive into the Sequence "x x 1 x 2"
The seemingly simple sequence "x x 1 x 2" might appear innocuous at first glance. However, its ambiguity opens the door to a fascinating exploration of mathematical patterns, logical reasoning, and the power of interpretation. This article will delve into the various potential meanings and interpretations of this sequence, exploring different mathematical contexts and demonstrating how seemingly simple patterns can lead to complex and insightful conclusions. We'll examine potential solutions, discuss the limitations of incomplete data, and ultimately, highlight the importance of context in problem-solving. This exploration will be valuable for anyone interested in mathematics, logic, and critical thinking.
Potential Interpretations of "x x 1 x 2"
The lack of context surrounding "x x 1 x 2" makes it difficult to definitively determine its meaning. However, we can approach this sequence from several perspectives, each yielding different interpretations and potential solutions:
1. As a Numerical Sequence: Identifying Patterns and Rules
The most straightforward approach is to treat the sequence as a numerical pattern. The presence of "x" indicates an unknown value. We can hypothesize potential rules governing the sequence's progression:
-
Linear Progression: Could the sequence follow a simple linear rule, where a constant value is added or subtracted at each step? However, the jump from 1 to 2 suggests this isn't a consistent linear progression.
-
Quadratic or Higher-Order Progression: More complex patterns might involve quadratic or even higher-order functions. The sequence might be a subset of a larger, more intricate mathematical relationship. Without more data points, identifying the underlying function is challenging.
-
Geometric Progression: A geometric progression involves multiplying by a constant value. This seems unlikely given the mix of x values and integers.
-
Recursive Relationship: The sequence could be defined recursively, meaning each term depends on the previous term(s). For instance, a rule like "x<sub>n</sub> = f(x<sub>n-1</sub>)" could govern the progression. However, without knowing the function "f," we cannot determine the values of x or the next term.
2. As a Symbolic Representation: Exploring Abstract Meanings
The "x" variable introduces an element of abstraction. Instead of representing a numerical value, "x" might symbolize a concept or variable within a larger system.
-
Variables in an Equation: "x x 1 x 2" could be a fragment of a larger mathematical equation or formula. For example, it might represent a series of operations where "x" acts as an operand or a coefficient.
-
Placeholders in a Code: In computer programming or coding contexts, "x" often serves as a placeholder for variables or data yet to be defined. The sequence could be part of an algorithm or a code snippet where the "x" values need to be determined based on the program's logic.
-
Representation of Sets or Groups: "x" might symbolize elements within a set or group. The sequence could be a representation of a mathematical structure like a group or a ring, where "x" represents unspecified elements under certain operations.
3. Considering Contextual Clues: The Importance of Additional Information
The critical limitation of our analysis is the absence of context. The sequence's meaning significantly depends on its origin and the broader problem it represents. Additional information could clarify its nature. For example:
-
Source of the Sequence: Where did this sequence originate? Knowing the context—a mathematics puzzle, a programming exercise, a research paper—would significantly impact its interpretation.
-
Surrounding Numbers: Are there numbers preceding or following this sequence? These additional numbers might reveal a pattern or a rule governing the whole sequence.
-
Type of Problem: Is this a sequence-finding problem, a coding challenge, or part of a larger mathematical problem? Understanding the problem statement is essential to interpreting the sequence correctly.
Mathematical Approaches and Limitations
Let's explore a few mathematical approaches to analyzing numerical sequences in general, highlighting the limitations when dealing with incomplete data like "x x 1 x 2":
1. Finite Differences Method
This method helps to identify the type of polynomial function generating a numerical sequence. We calculate the differences between consecutive terms, then the differences between those differences, and so on. If the differences eventually become constant, it suggests a polynomial of a specific degree. However, with only four terms and two unknowns, this method is insufficient to determine the generating function.
2. Regression Analysis
If we assume a functional relationship between the positions in the sequence and the values, we could use regression analysis. This involves fitting a mathematical model to the data. However, with only two data points (1 and 2) and two unknown 'x' values, the degrees of freedom are too low for meaningful regression. Multiple models could fit the data equally well, highlighting the uncertainty.
3. Pattern Recognition and Inference
Humans are adept at pattern recognition. We might intuitively look for repeating patterns, alternating patterns, or other common mathematical structures. However, with limited information, such inferences remain speculative. Several plausible, but unprovable, patterns might appear equally likely.
Illustrative Examples: Sequences with Similar Structure
To better understand the challenges and possibilities, let's look at examples of sequences with similar structures:
-
Example 1: Let's assume the sequence is a simple alternation: x, x, 1, x, 2, x, 3, x... In this case, the "x" values might be constant or follow their own pattern, providing clarity.
-
Example 2: Consider the sequence x, x, 1, 2, x, x, 3, 4... Here, the pattern involves pairs of numbers, one of which is 'x', indicating that there could be a rule for determining the 'x' value based on its position or the preceding integers.
These examples show how adding context and additional data points significantly alter the possible interpretations.
Frequently Asked Questions (FAQ)
Q: Can we definitively solve for the value of "x"?
A: No, without additional context or information, it's impossible to definitively solve for "x." There are infinitely many possibilities.
Q: What are some common mistakes in approaching this type of problem?
A: Assuming a simple linear pattern without sufficient evidence is a common mistake. Jumping to conclusions based on limited data without exploring other possibilities is another potential pitfall.
Q: What mathematical concepts are relevant to solving this type of sequence problem?
A: Relevant concepts include: sequence analysis, pattern recognition, regression analysis, finite differences, recursive relationships, and polynomial fitting. However, the applicability of these depends on the availability of sufficient data.
Q: How can I improve my ability to solve similar sequence puzzles?
A: Practice solving various sequence puzzles, explore different mathematical approaches, and develop your intuition for recognizing patterns. Also, critically examine assumptions and consider alternative explanations.
Conclusion: The Power of Context and Critical Thinking
The seemingly simple sequence "x x 1 x 2" serves as a powerful illustration of the importance of context and critical thinking in problem-solving. Without additional information, numerous plausible interpretations exist, highlighting the limitations of incomplete data. To successfully analyze such sequences, we need to consider the source, surrounding data, and the type of problem being addressed. This exercise underscores the need for careful consideration, the exploration of multiple perspectives, and the avoidance of premature conclusions based on limited information. The ability to approach such problems methodically, exploring different mathematical and logical possibilities, is a skill crucial for success in many fields, from mathematics and computer science to data analysis and scientific research. The journey of unraveling the mystery of "x x 1 x 2" is a microcosm of the larger process of scientific inquiry—one that emphasizes the power of observation, deduction, and the acceptance of ambiguity when sufficient evidence is lacking.
Latest Posts
Latest Posts
-
When Does The Ymca Open
Sep 16, 2025
-
Les Animaux De La Foret
Sep 16, 2025
-
When Was Duct Tape Invented
Sep 16, 2025
-
How To Right A Monologue
Sep 16, 2025
-
Nursing Diagnosis Related To Infection
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X X 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.