1 E Ln 1 E
monicres
Sep 24, 2025 · 6 min read
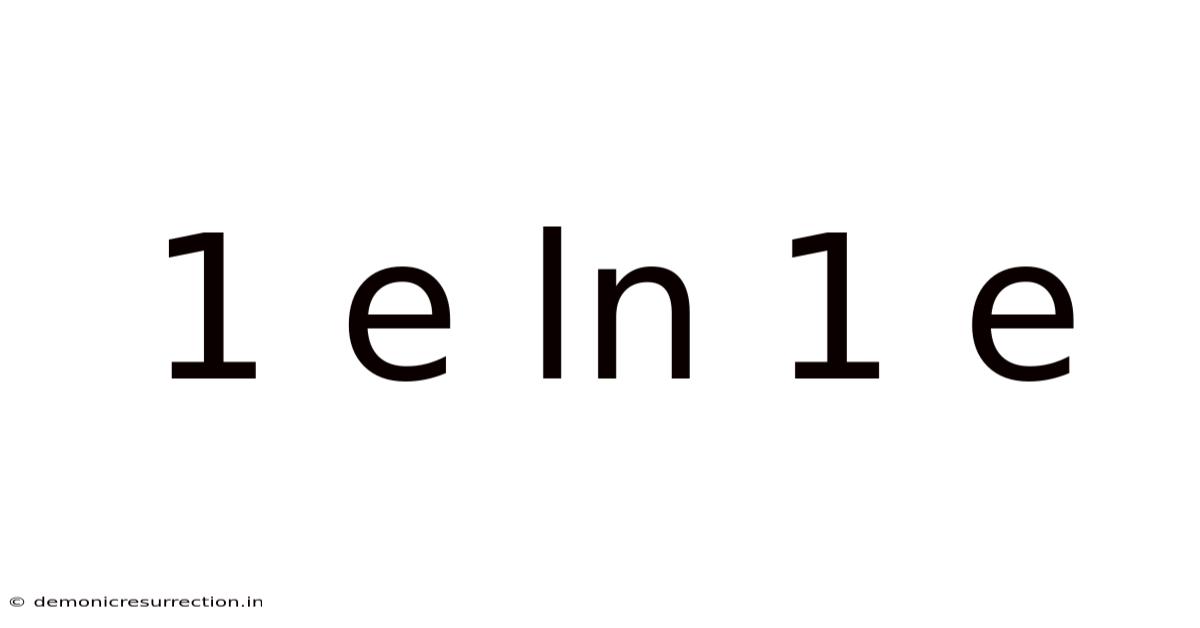
Table of Contents
Unveiling the Enigma: A Deep Dive into 1 * e^ln(1/e)
The expression 1 * e^ln(1/e) might seem intimidating at first glance, especially for those less familiar with logarithmic and exponential functions. However, this seemingly complex equation is a fantastic opportunity to explore fundamental concepts in mathematics, specifically the interplay between exponential functions and their inverse, logarithmic functions. Understanding this expression unlocks a deeper appreciation for the elegance and interconnectedness of mathematical concepts. This article will not only solve the equation but also provide a comprehensive explanation of the underlying principles, making it accessible even to those with a basic understanding of algebra.
Introduction: The Dance Between e and ln
At the heart of this equation lies the mathematical constant e, also known as Euler's number, approximately equal to 2.71828. e is the base of the natural logarithm, denoted as ln. The natural logarithm is the inverse function of the exponential function with base e. This inverse relationship is the key to simplifying our expression. In simpler terms, if you have a function that involves e raised to a power, and that power happens to be a natural logarithm, these operations effectively cancel each other out, leading to significant simplification.
We'll break down the expression step-by-step, explaining the rules and principles applied at each stage. By the end, you will not only understand how to solve this specific equation but also gain a solid grasp of the underlying mathematical concepts, empowering you to tackle similar problems with confidence.
Understanding the Components: e and ln
Before delving into the solution, let's refresh our understanding of e and ln:
-
e (Euler's number): A transcendental number approximately equal to 2.71828. It's a fundamental constant in mathematics, appearing in various areas like calculus, probability, and compound interest. The exponential function e<sup>x</sup> represents continuous exponential growth.
-
ln (Natural Logarithm): The logarithm to the base e. It's the inverse function of the exponential function e<sup>x</sup>. This means that ln(e<sup>x</sup>) = x and e<sup>ln(x)</sup> = x (for x > 0). The natural logarithm describes the time needed for exponential growth to reach a certain value.
Step-by-Step Solution: Deconstructing 1 * e^ln(1/e)
Now, let's systematically solve 1 * e^ln(1/e):
-
Simplify the Argument of the Logarithm: The expression contains ln(1/e). Recall the logarithmic property: ln(a/b) = ln(a) - ln(b). Applying this, we get:
ln(1/e) = ln(1) - ln(e)
-
Evaluate the Logarithms: We know that ln(1) = 0 (since e<sup>0</sup> = 1) and ln(e) = 1 (since e<sup>1</sup> = e). Therefore:
ln(1/e) = 0 - 1 = -1
-
Substitute Back into the Original Expression: Now we substitute this simplified value back into the original expression:
1 * e^ln(1/e) = 1 * e<sup>-1</sup>
-
Simplify the Exponential Expression: Recall that e<sup>-1</sup> is the same as 1/e. Therefore:
1 * e<sup>-1</sup> = 1 * (1/e) = 1/e
-
Final Answer: The simplified form of the expression 1 * e^ln(1/e) is 1/e. This is the exact answer, and its approximate numerical value is around 0.36788.
Deeper Mathematical Insights: Exploring the Inverse Relationship
The solution highlights the crucial inverse relationship between the exponential function (with base e) and the natural logarithm. The fact that e<sup>ln(x)</sup> = x for x > 0 is a fundamental property used extensively in calculus and other advanced mathematical fields. This property allowed us to effectively cancel out the exponential and logarithmic functions in our equation, simplifying it to a straightforward fraction.
The expression also subtly showcases the concept of exponential decay. The negative exponent in e<sup>-1</sup> indicates a decay process rather than growth. This is reflected in the final answer being a fraction less than 1.
Practical Applications: Beyond the Theoretical
While the expression 1 * e^ln(1/e) might seem purely theoretical, the underlying principles have wide-ranging practical applications:
-
Compound Interest: The number e plays a crucial role in calculating continuously compounded interest. Understanding exponential functions is vital for financial modeling and investment analysis.
-
Radioactive Decay: Exponential decay is used to model radioactive decay, where the amount of a radioactive substance decreases exponentially over time.
-
Population Growth/Decline: Exponential functions can model population growth or decline under specific conditions.
-
Statistical Analysis: The natural logarithm is frequently used in statistical analysis, particularly in transforming data to improve normality or simplifying complex relationships.
-
Signal Processing: Exponential functions and their logarithmic counterparts are crucial in signal processing for tasks such as filtering and data compression.
-
Differential Equations: Solving many differential equations that describe real-world phenomena (e.g., cooling of an object, growth of a bacterial population) often involves exponential and logarithmic functions.
Frequently Asked Questions (FAQ)
-
What if the expression was e^ln(e/1)? Following the same principles, ln(e/1) = ln(e) - ln(1) = 1 - 0 = 1. Therefore, e<sup>ln(e/1)</sup> = e<sup>1</sup> = e.
-
Can I use a calculator to solve this? Yes, you can calculate the numerical approximation of 1/e using a scientific calculator. However, understanding the underlying mathematical principles is more valuable than simply obtaining a numerical result.
-
Why is the natural logarithm important? The natural logarithm is important because it's the inverse of the exponential function with base e. This inverse relationship allows for simplification in many mathematical contexts and is crucial for calculus, particularly in differentiation and integration. It also provides a natural way to analyze processes that involve continuous growth or decay.
-
What are some other examples of this type of simplification? Many similar simplifications are possible using the properties of logarithms and exponents. For instance, e<sup>ln(x²)</sup> simplifies to x², and ln(e<sup>3x</sup>) simplifies to 3x. The key is to identify and apply the appropriate logarithmic and exponential rules.
Conclusion: Mastering the Fundamentals
Solving the expression 1 * e^ln(1/e) is more than just an exercise in calculation. It’s a journey of exploration into the fundamental relationship between exponential and logarithmic functions. By understanding the interplay between e and ln, you equip yourself with powerful tools applicable in various fields. Remember, mastering the fundamental concepts is crucial, paving the way for tackling more complex mathematical challenges in the future. The seemingly simple equation presented here serves as a gateway to a deeper understanding of a significant area of mathematics. The next time you encounter a similar expression, you'll be ready to approach it with confidence and clarity.
Latest Posts
Latest Posts
-
Pe Games For High School
Sep 24, 2025
-
Example Of Poetry Analysis Paper
Sep 24, 2025
-
Dna Major And Minor Groove
Sep 24, 2025
-
Erlenmeyer Flask And Conical Flask
Sep 24, 2025
-
Closed End Vs Open End
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 E Ln 1 E . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.