2 1 4 X 2
monicres
Sep 14, 2025 · 6 min read
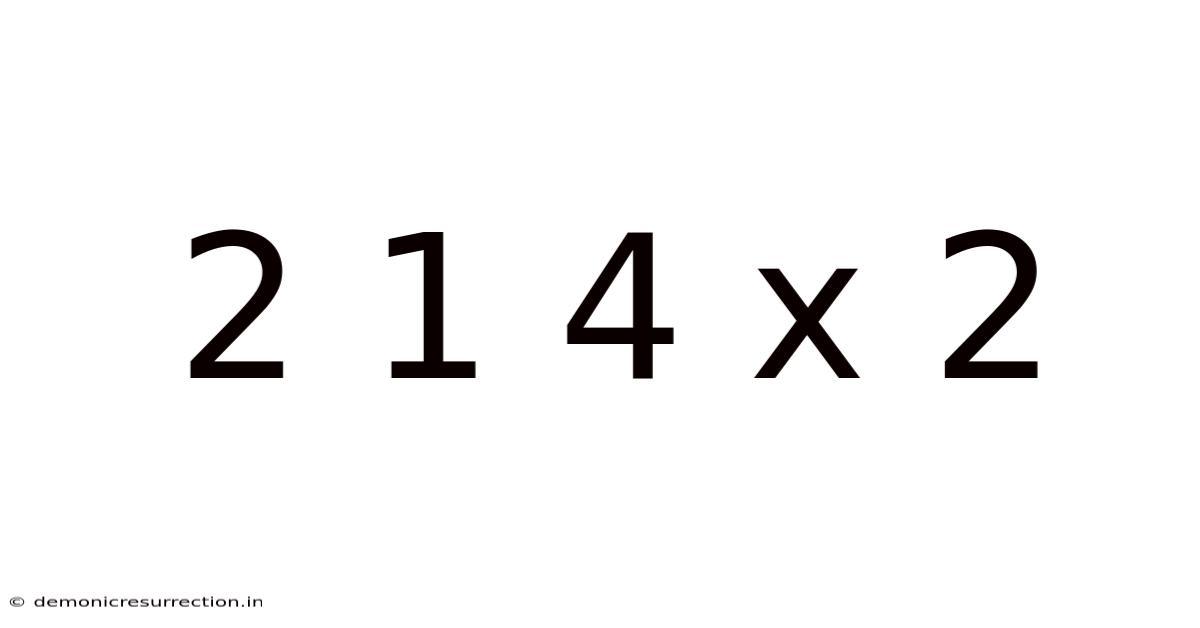
Table of Contents
Decoding 2 1 4 x 2: Exploring Multiplication, Fractions, and Mixed Numbers
This article delves into the seemingly simple mathematical expression "2 1/4 x 2," exploring its various interpretations and solutions. We'll unpack the concepts of mixed numbers, improper fractions, and multiplication of fractions, offering a comprehensive understanding suitable for learners of all levels. Understanding this calculation provides a strong foundation for more complex mathematical operations. This guide will not only show you how to solve the problem but also why the methods work, equipping you with the knowledge to tackle similar problems with confidence.
Understanding Mixed Numbers and Improper Fractions
Before we tackle the multiplication, let's clarify the core component of our problem: the mixed number "2 1/4." A mixed number combines a whole number and a fraction. In this case, we have 2 whole units and 1/4 of another unit.
To perform multiplication efficiently, it's often easier to convert mixed numbers into improper fractions. An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). To convert 2 1/4 into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 2 x 4 = 8
- Add the numerator: 8 + 1 = 9
- Keep the same denominator: The denominator remains 4.
Therefore, 2 1/4 is equivalent to the improper fraction 9/4. This conversion is crucial for simplifying our multiplication.
Multiplying Fractions: A Step-by-Step Guide
Now that we've converted our mixed number, let's tackle the multiplication: 9/4 x 2. Multiplying fractions involves multiplying the numerators together and the denominators together. However, before we proceed, let's represent the whole number 2 as a fraction: 2/1. This makes the multiplication process clearer and consistent.
Our calculation now looks like this: (9/4) x (2/1).
Here's the step-by-step solution:
- Multiply the numerators: 9 x 2 = 18
- Multiply the denominators: 4 x 1 = 4
- Resulting improper fraction: This gives us the improper fraction 18/4.
This improper fraction represents our answer, but it's generally preferred to express the answer as a simplified mixed number or a decimal.
Simplifying the Improper Fraction and Converting to a Mixed Number
The improper fraction 18/4 can be simplified. To simplify, we find the greatest common divisor (GCD) of the numerator (18) and the denominator (4). The GCD of 18 and 4 is 2. We divide both the numerator and the denominator by the GCD:
18 ÷ 2 = 9 4 ÷ 2 = 2
This simplifies our improper fraction to 9/2.
Now, let's convert this improper fraction (9/2) back into a mixed number:
- Divide the numerator by the denominator: 9 ÷ 2 = 4 with a remainder of 1.
- The quotient becomes the whole number: 4
- The remainder becomes the numerator: 1
- The denominator remains the same: 2
Therefore, 9/2 is equivalent to the mixed number 4 1/2. This is our final answer.
Alternative Method: Distributive Property
Another approach to solving 2 1/4 x 2 involves using the distributive property of multiplication. This method can be particularly useful when dealing with more complex mixed numbers. We can break down the multiplication as follows:
2 1/4 x 2 = (2 + 1/4) x 2
Now, we distribute the 2 to both parts of the mixed number:
(2 x 2) + (1/4 x 2) = 4 + 2/4
Simplifying the fraction 2/4 to 1/2, we get:
4 + 1/2 = 4 1/2
This method yields the same result as our previous method, demonstrating the versatility of different mathematical approaches.
Decimal Representation
While mixed numbers and fractions are common in mathematical contexts, it's also useful to understand the decimal equivalent of our answer. To convert 4 1/2 to a decimal, we simply divide the numerator (1) by the denominator (2):
1 ÷ 2 = 0.5
Therefore, 4 1/2 is equal to 4.5. This decimal representation can be particularly helpful when working with calculators or in applications where decimal values are preferred.
Illustrative Examples and Practical Applications
Understanding the multiplication of mixed numbers has wide-ranging applications in everyday life and various fields:
- Baking and Cooking: Recipes often require multiplying ingredient quantities. For example, if a recipe calls for 2 1/4 cups of flour and you want to double the recipe, you'd need to calculate 2 1/4 x 2.
- Construction and Measurement: In construction, accurate measurements are vital. Calculating the length of multiple pieces of material often involves multiplying mixed numbers.
- Finance and Budgeting: Dividing or multiplying budgets and calculating interest often involves working with fractions and mixed numbers.
- Geometry and Area Calculations: Determining the area of a rectangle or other shapes might involve multiplying mixed numbers representing the length and width.
Frequently Asked Questions (FAQ)
Q: Can I multiply the whole number and the fraction separately before combining them?
A: While not incorrect, this method can be less efficient. Converting to an improper fraction simplifies the multiplication process and minimizes the risk of errors. However, the distributive property, as demonstrated above, is a valid and sometimes easier alternative.
Q: What if the whole number being multiplied is not 2?
A: The process remains the same. Convert the mixed number to an improper fraction, represent the whole number as a fraction (e.g., 3 becomes 3/1), multiply the fractions, simplify, and convert back to a mixed number if needed.
Q: Is there a quicker way to solve this type of problem?
A: While the steps outlined provide a thorough understanding, with practice, you can streamline the process. You can mentally convert the mixed number to an improper fraction and perform the multiplication more quickly.
Q: What are some common mistakes to avoid when multiplying mixed numbers?
A: Common mistakes include forgetting to convert mixed numbers to improper fractions, incorrectly multiplying the numerators and denominators, and failing to simplify the resulting fraction. Careful attention to each step minimizes these errors.
Conclusion
This in-depth exploration of "2 1/4 x 2" has unveiled the underlying mathematical principles involved in multiplying mixed numbers. By converting mixed numbers to improper fractions, performing the multiplication, simplifying the result, and converting back to a mixed number or decimal, we arrive at the accurate solution of 4 1/2 or 4.5. Mastering this fundamental concept lays a solid foundation for tackling more complex mathematical problems encountered in various academic and real-world applications. Remember to practice regularly to build confidence and proficiency in handling fractions and mixed numbers with ease.
Latest Posts
Latest Posts
-
Balloon Frame Vs Platform Frame
Sep 14, 2025
-
2 5 M En Pied
Sep 14, 2025
-
Purchase Of Supplies On Account
Sep 14, 2025
-
Picture Of A Nervous System
Sep 14, 2025
-
Convertir Des Litres En Ml
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 1 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.