20 000 Divided By 12
monicres
Sep 13, 2025 · 5 min read
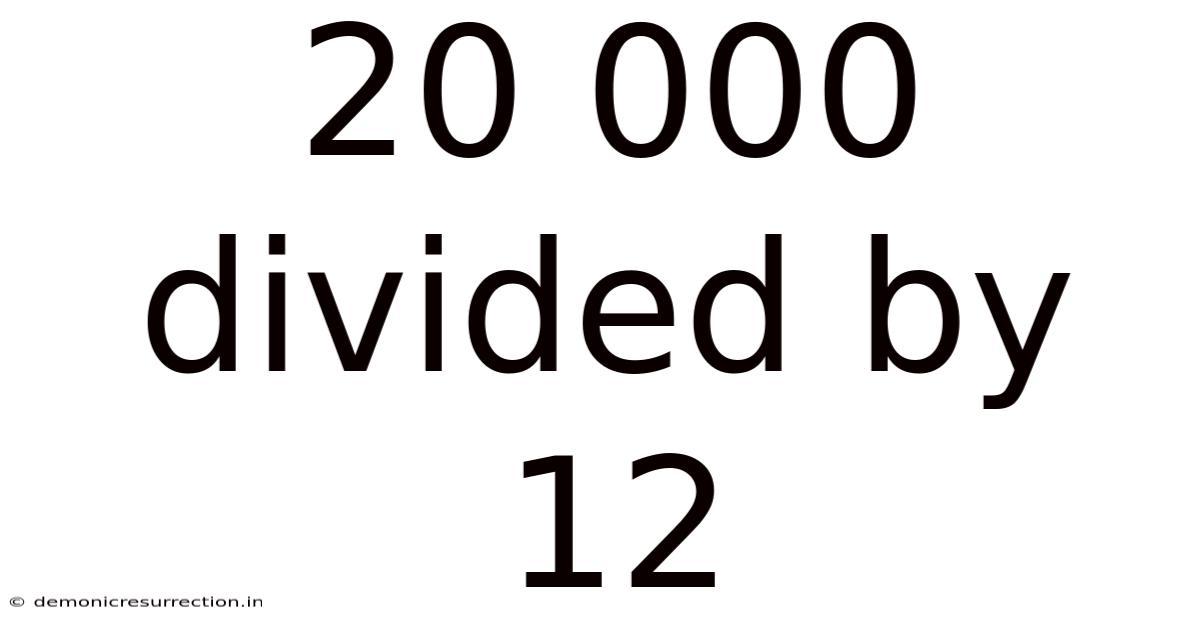
Table of Contents
20,000 Divided by 12: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 20,000 divided by 12, delving far beyond the immediate answer. We'll unravel the process, discuss different methods of solving this division problem, explore its real-world applications, and delve into the underlying mathematical concepts. This comprehensive guide is designed for anyone, from students strengthening their arithmetic skills to adults seeking to refresh their knowledge of fundamental mathematics. Understanding division, particularly with larger numbers, is crucial for various aspects of life, including budgeting, measurement, and problem-solving.
Understanding the Problem: 20,000 ÷ 12
The problem, 20,000 divided by 12 (or 20,000 ÷ 12), asks: "How many times does 12 fit into 20,000?" The answer represents the quotient, while any remaining amount is the remainder. This seemingly straightforward question can lead to deeper understanding of several mathematical principles.
Methods for Solving 20,000 ÷ 12
Several methods can be used to solve this division problem:
1. Long Division: This is the most common method taught in schools.
1666 R 8
12 | 20000
-12
----
80
-72
----
80
-72
----
80
-72
----
8
This shows that 12 goes into 20,000 a total of 1666 times with a remainder of 8. Therefore, 20,000 ÷ 12 = 1666 with a remainder of 8. Or, expressed as a mixed number: 1666 ⁸⁄₁₂ which simplifies to 1666 ⅔.
2. Using a Calculator: The easiest and fastest method, simply input 20000 ÷ 12 into any calculator to obtain the result: 1666.666666... This is a repeating decimal.
3. Breaking Down the Problem: We can simplify the problem by breaking down 20,000 into more manageable numbers. For example:
- Divide 20,000 by 10: 2000
- Divide 2000 by 2: 1000
- Now divide 1000 by 6 (since 12 = 2 x 6): This gives approximately 166.666...
- Now we must consider the approximation.
4. Using Fractions: We can express the problem as a fraction: 20,000/12. This fraction can then be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD of 20,000 and 12 is 4. Simplifying, we get 5000/3. This is equivalent to 1666 ⅔.
Real-World Applications of Division
The ability to perform division, particularly with larger numbers, has numerous real-world applications:
-
Budgeting: Dividing a monthly budget among different expenses (rent, food, transportation, etc.) requires division. For example, if your monthly income is $20,000 and you want to allocate it equally among 12 months, you'd perform 20,000 ÷ 12 to determine your monthly budget.
-
Measurement and Conversion: Converting units of measurement often involves division. For example, converting total inches of rainfall over 12 months into average monthly rainfall requires division. Similarly, converting kilometers into miles involves division (or multiplication by a conversion factor which is effectively a division).
-
Equal Sharing: Dividing resources equally among a group of people is a common application. For example, if 20,000 candies need to be distributed evenly among 12 children, each child would receive 1666 candies with 8 candies remaining.
-
Averaging: Calculating average values involves division. For instance, finding the average daily sales over 12 days requires summing up the daily sales and then dividing by 12.
-
Rate and Ratio Problems: Many rate and ratio problems in fields like science, engineering, and finance rely on division. Determining unit costs (cost per item), speed (distance divided by time), and density (mass divided by volume) all involve division.
-
Finance: Calculating interest, amortization schedules, and return on investment (ROI) often involve complex calculations that include division.
-
Data Analysis: In statistical analysis, calculating means, medians, and other descriptive statistics often necessitate division.
Deeper Mathematical Concepts
Solving 20,000 ÷ 12 also allows us to explore some deeper mathematical concepts:
-
Divisibility Rules: While not directly applicable to this specific problem in its entirety, understanding divisibility rules can help simplify similar problems with smaller numbers. For example, knowing that a number is divisible by 12 if it's divisible by both 3 and 4 can aid in faster mental calculations in simpler scenarios.
-
Prime Factorization: The prime factorization of 12 (2 x 2 x 3) and 20,000 (2⁵ x 5⁴) could be used to simplify the fraction 20,000/12 before performing the division. This approach shows the fundamental building blocks of the numbers involved.
-
Decimal Representation: The result, 1666.666..., highlights the concept of repeating decimals. Understanding why certain fractions result in repeating decimals is a key concept in number theory.
-
Remainders: The remainder of 8 in this division problem represents the amount left over after dividing 20,000 as equally as possible among 12 groups. Understanding remainders is crucial in many real-world situations where perfect division isn't possible.
Frequently Asked Questions (FAQs)
-
What is the exact answer to 20,000 divided by 12? The exact answer is 1666 ⅔ or 1666.666... (a repeating decimal).
-
What is the remainder when 20,000 is divided by 12? The remainder is 8.
-
How can I calculate this without a calculator? Long division is the most reliable method for manual calculation.
-
What are some real-world situations where I might use this calculation? Budgeting, measurement conversions, equal sharing, averaging, and various rate and ratio problems are just a few examples.
-
Why is the answer a repeating decimal? Because the fraction 5000/3 (the simplified form of 20000/12) has a denominator that is not a factor of 10 or any power of 10. This often leads to a repeating decimal representation.
Conclusion
The seemingly simple calculation of 20,000 divided by 12 opens doors to a broader understanding of division, its various methods of solution, and its wide-ranging applications in everyday life. Mastering division is a fundamental skill that transcends the classroom, proving invaluable in navigating numerous practical situations. This exploration not only provides the answer but also fosters a deeper appreciation for the mathematical principles underlying this seemingly straightforward operation, encouraging further exploration of mathematical concepts and their real-world relevance. From budgeting to scientific calculations, the ability to confidently perform and understand division forms a crucial building block for effective problem-solving and informed decision-making across various aspects of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 000 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.