7 7/10 As A Decimal
monicres
Sep 14, 2025 · 5 min read
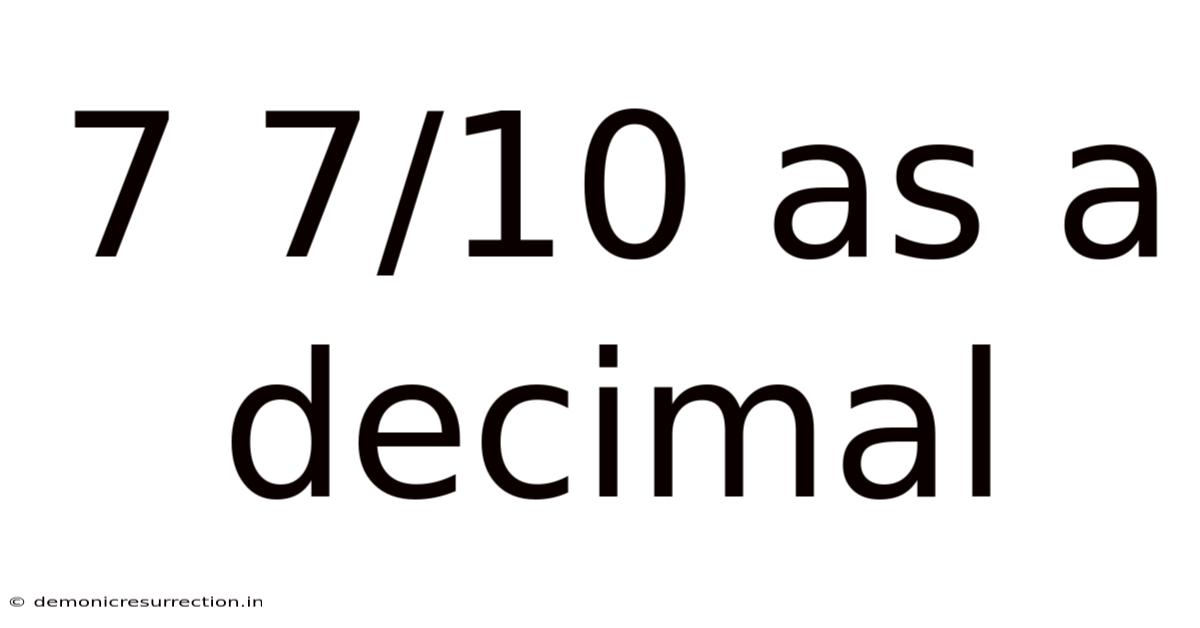
Table of Contents
7 7/10 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article provides a thorough understanding of how to convert the mixed number 7 7/10 into its decimal equivalent, explaining the process step-by-step and exploring the underlying principles. We will also delve into the broader context of fraction-to-decimal conversions, addressing common misconceptions and offering practical examples to solidify your understanding. This guide is designed for learners of all levels, from those just beginning their journey with fractions to those seeking to refresh their knowledge.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly review the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 7 7/10. The whole number (7 in this case) represents the complete units, while the fraction (7/10) represents a part of a unit.
A decimal, on the other hand, represents a number using a base-10 system. The digits to the right of the decimal point represent fractions of powers of 10 (tenths, hundredths, thousandths, etc.). For example, 0.7 represents seven-tenths (7/10), and 0.07 represents seven-hundredths (7/100).
Converting 7 7/10 to a Decimal: A Step-by-Step Approach
Converting 7 7/10 to a decimal is straightforward. We can approach this conversion in two main ways:
Method 1: Direct Conversion
This method directly addresses the fraction part of the mixed number. The fraction 7/10 already has a denominator that is a power of 10 (10<sup>1</sup>). Therefore, converting it to a decimal is simply a matter of placing the numerator (7) to the right of the decimal point, preceded by the whole number part (7).
Therefore, 7 7/10 = 7.7
Method 2: Converting the Fraction Separately Then Adding
This method involves converting the fraction to a decimal first, and then adding the whole number.
-
Convert the fraction: The fraction is 7/10. To convert a fraction to a decimal, we divide the numerator (7) by the denominator (10): 7 ÷ 10 = 0.7
-
Add the whole number: Now, add the whole number part (7) to the decimal equivalent of the fraction (0.7): 7 + 0.7 = 7.7
Both methods yield the same result: 7 7/10 is equivalent to 7.7
Understanding the Process: Why it Works
The success of these methods hinges on our understanding of place value in the decimal system. The denominator of the fraction 7/10 indicates that we are dealing with tenths. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a progressively smaller fraction of 1: tenths, hundredths, thousandths, and so on. Since the denominator is 10, the numerator (7) directly occupies the tenths place.
Expanding the Concept: Converting Other Fractions to Decimals
The methods described above can be applied to other fractions, but some require extra steps. Here’s a breakdown of different scenarios:
-
Fractions with denominators that are powers of 10 (10, 100, 1000, etc.): These are the easiest to convert. Simply place the numerator to the right of the decimal point, adjusting for the number of zeros in the denominator. For example:
- 3/10 = 0.3
- 27/100 = 0.27
- 456/1000 = 0.456
-
Fractions with denominators that are not powers of 10: These require long division. Divide the numerator by the denominator. For example, to convert 3/4 to a decimal:
3 ÷ 4 = 0.75
-
Improper Fractions: Improper fractions (where the numerator is greater than or equal to the denominator) result in a decimal greater than or equal to 1. For example:
11/5 = 2.2 (because 11 divided by 5 is 2 with a remainder of 1, which is 1/5 or 0.2)
-
Mixed Numbers: As demonstrated with 7 7/10, convert the fraction part to a decimal and then add it to the whole number.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is valuable across numerous fields:
-
Finance: Calculating interest rates, discounts, and profit margins often involve converting fractions to decimals.
-
Science: Scientific measurements and data analysis frequently use decimals for precision and ease of calculation.
-
Engineering: Design and construction projects rely heavily on precise measurements expressed as decimals.
-
Everyday life: From calculating tips to measuring ingredients in a recipe, understanding decimals simplifies many daily tasks.
Frequently Asked Questions (FAQ)
Q1: What if the decimal representation is recurring (repeating)?
A1: Some fractions, when converted to decimals, result in non-terminating, repeating decimals (e.g., 1/3 = 0.333...). These can be represented using a bar over the repeating digits (e.g., 0.3̅).
Q2: Can I use a calculator to convert fractions to decimals?
A2: Yes, most calculators have a fraction-to-decimal conversion function. Simply enter the fraction and press the appropriate button.
Q3: Is there a way to convert decimals back to fractions?
A3: Yes, absolutely! This involves identifying the place value of the decimal digits and constructing a fraction based on those values. For example, 0.25 can be expressed as 25/100, which simplifies to 1/4.
Q4: Why is understanding fraction-to-decimal conversion important?
A4: It's fundamental to arithmetic and necessary for a clear understanding of numerical representation and manipulation. Proficiency in this skill strengthens your mathematical foundation and enhances problem-solving abilities in diverse contexts.
Conclusion
Converting 7 7/10 to its decimal equivalent, 7.7, is a simple yet illustrative example of a vital mathematical process. Understanding this conversion, along with the broader principles of converting fractions to decimals and decimals to fractions, is crucial for success in various academic and real-world applications. By mastering this skill, you enhance your numerical fluency and build a solid foundation for more complex mathematical concepts. Remember to practice regularly to solidify your understanding and increase your confidence in tackling more challenging fraction-to-decimal conversions. The more you practice, the more intuitive this process will become. From simple everyday calculations to complex scientific problems, the ability to seamlessly transition between fractions and decimals is a powerful tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
Samuel Beckett Warten Auf Godot
Sep 15, 2025
-
Mammals Amphibians Reptiles Birds Fish
Sep 15, 2025
-
How Tall Is 1 75 Meters
Sep 15, 2025
-
Map Of Huckleberry Finns Journey
Sep 15, 2025
-
44 50 As A Percentage
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 7 7/10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.