9 20 As A Percent
monicres
Sep 17, 2025 · 5 min read
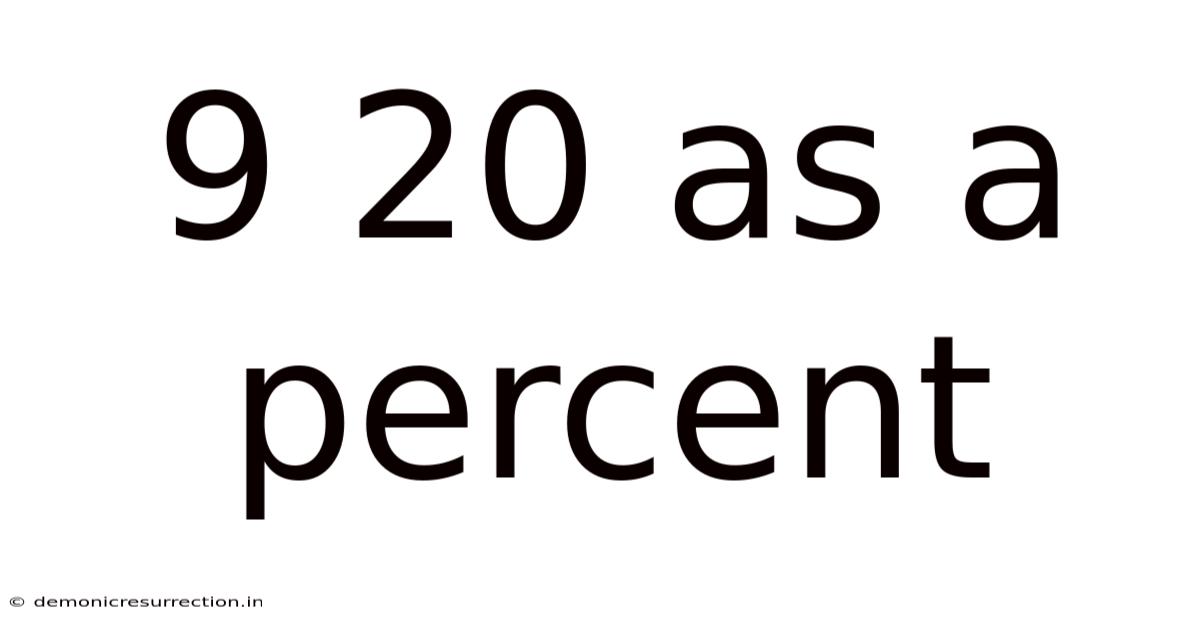
Table of Contents
9/20 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 9/20 into a percentage, exploring different methods and offering a deeper understanding of the underlying principles. We'll also address common misconceptions and provide practical examples to solidify your understanding. By the end, you’ll not only know that 9/20 equals 45%, but you'll also grasp the broader concept of fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 9/20, 9 represents the number of parts and 20 represents the total number of parts.
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Percentages are often used to represent proportions, rates, or changes. For example, 45% means 45 out of 100.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 9/20 to a percentage involves transforming the fraction into an equivalent fraction with a denominator of 100.
-
Find the Equivalent Fraction: To change the denominator from 20 to 100, we multiply both the numerator and the denominator by 5 (because 100 ÷ 20 = 5).
(9 × 5) / (20 × 5) = 45/100
-
Express as a Percentage: Since a percentage is a fraction out of 100, 45/100 is directly equivalent to 45%. Therefore, 9/20 as a percent is 45%.
Method 2: Using Decimal Conversion as an Intermediate Step
This method involves two steps: first converting the fraction to a decimal, and then converting the decimal to a percentage.
-
Convert the Fraction to a Decimal: Divide the numerator (9) by the denominator (20).
9 ÷ 20 = 0.45
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.45 × 100 = 45%
Therefore, 9/20 as a percentage is again 45%. This method is particularly useful when dealing with fractions that don't easily convert to an equivalent fraction with a denominator of 100.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion where one ratio represents the fraction 9/20 and the other represents the unknown percentage (x/100).
-
Set up the Proportion:
9/20 = x/100
-
Solve for x: Cross-multiply to solve for x.
9 × 100 = 20 × x 900 = 20x x = 900 ÷ 20 x = 45
Therefore, x = 45, meaning 9/20 is equal to 45%. This method reinforces the understanding of ratios and proportions, demonstrating the equivalence between the fraction and the percentage.
Understanding the Concept of Proportionality
The ability to convert fractions to percentages hinges on understanding proportionality. A proportion is a statement that two ratios are equal. In the context of converting 9/20 to a percentage, we are essentially finding an equivalent ratio where the denominator is 100. This equivalence highlights the fundamental relationship between fractions and percentages. Both represent parts of a whole, expressed differently. The percentage simply provides a standardized way of expressing the proportion relative to 100.
Practical Applications of Percentage Conversions
The skill of converting fractions to percentages has wide-ranging practical applications:
- Finance: Calculating interest rates, discounts, and tax amounts often involves converting fractions to percentages.
- Statistics: Expressing data as percentages allows for easy comparison and interpretation of proportions within a dataset.
- Science: Representing experimental results and error margins often utilizes percentages.
- Everyday Life: Understanding percentages is essential for calculating tips, comparing prices, and interpreting various statistics encountered in daily life.
Common Misconceptions
Several common misconceptions can arise when working with fractions and percentages:
- Confusing Numerator and Denominator: Ensure you correctly identify the numerator (the part) and the denominator (the whole) before performing any calculations.
- Incorrect Multiplication/Division: Double-check your calculations to avoid errors in multiplying or dividing the numerator and denominator.
- Forgetting the Percentage Sign: Remember to always include the "%" symbol after the numerical value when expressing a percentage.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 9/20 to a percentage?
A: Yes, you can use a calculator to directly divide 9 by 20 (resulting in 0.45) and then multiply by 100 to get 45%.
Q: Are there other fractions that are equivalent to 45%?
A: Yes, any fraction that simplifies to 45/100 or 9/20 is equivalent to 45%. Examples include 135/300, 180/400, etc.
Q: What if the fraction has a larger numerator than the denominator?
A: If the numerator is larger than the denominator, the resulting percentage will be greater than 100%. This represents a value that exceeds the whole.
Q: How can I improve my understanding of fraction-to-percentage conversions?
A: Practice is key! Work through various examples, using different methods. Start with simpler fractions and gradually increase the complexity.
Conclusion
Converting 9/20 to a percentage illustrates a core mathematical concept with numerous practical applications. We have explored three distinct methods – direct conversion, decimal conversion, and using proportions – each offering a unique approach to solving this type of problem. By mastering these methods and understanding the underlying principles of proportionality, you’ll build a strong foundation in working with fractions and percentages, empowering you to tackle more complex mathematical challenges with confidence. Remember, consistent practice is the key to solidifying your understanding and building fluency in this essential skill.
Latest Posts
Latest Posts
-
If Function With 3 Conditions
Sep 17, 2025
-
Is Kazakhstan A Muslim Country
Sep 17, 2025
-
What Does A Lamb Represent
Sep 17, 2025
-
Amphibians Mammals Reptiles Birds Fish
Sep 17, 2025
-
What Is Bedmas In Math
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 9 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.