Gcf Of 12 And 18
monicres
Sep 17, 2025 · 5 min read
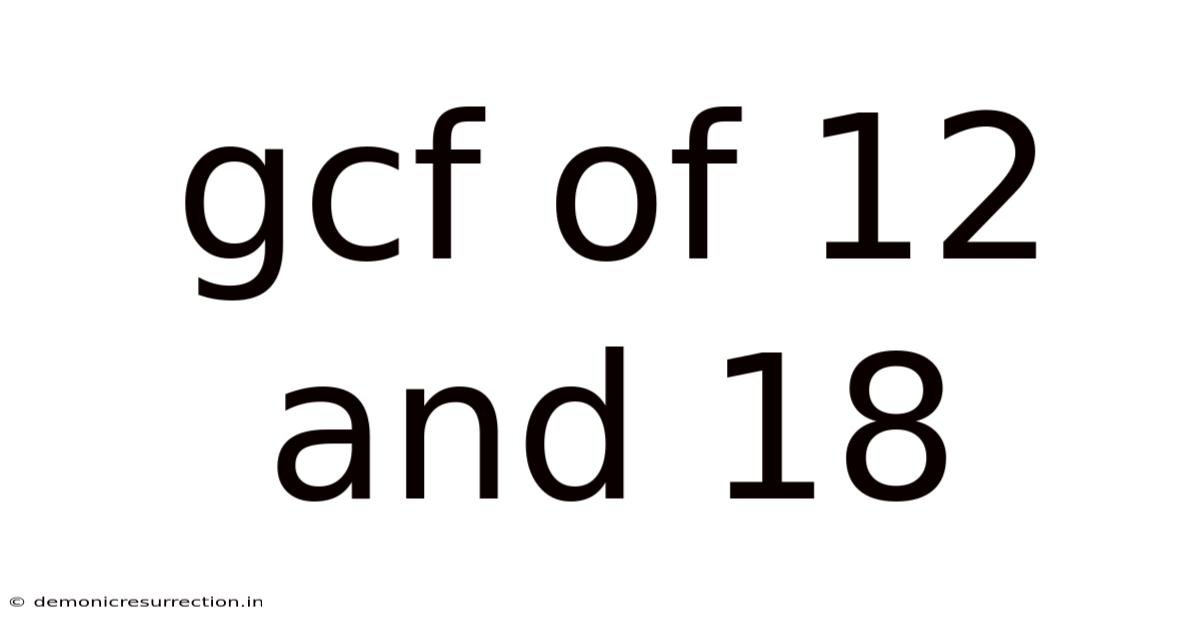
Table of Contents
Understanding the Greatest Common Factor (GCF) of 12 and 18: A Comprehensive Guide
Finding the greatest common factor (GCF) of two numbers, such as 12 and 18, is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving algebraic equations. This article will provide a comprehensive understanding of how to determine the GCF of 12 and 18, exploring multiple methods and delving into the underlying mathematical principles. We'll also examine the broader significance of GCFs and answer frequently asked questions. Understanding GCFs is crucial for building a solid foundation in mathematics and for tackling more advanced concepts later on.
Introduction to Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both. While straightforward for smaller numbers like 12 and 18, it becomes less efficient as the numbers get larger.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 18: 1, 2, 3, 6, 9, 18
Common Factors: 1, 2, 3, 6
Greatest Common Factor (GCF): 6
This method visually demonstrates the concept of common factors, making it ideal for beginners. However, for larger numbers, this method can become cumbersome and time-consuming.
Method 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. This method is more efficient than listing factors, particularly for larger numbers.
Prime Factorization of 12:
12 = 2 x 2 x 3 = 2² x 3
Prime Factorization of 18:
18 = 2 x 3 x 3 = 2 x 3²
To find the GCF using prime factorization, we identify the common prime factors and their lowest powers. Both 12 and 18 share a single '2' and a single '3'. Therefore:
GCF(12, 18) = 2¹ x 3¹ = 2 x 3 = 6
This method provides a systematic and efficient approach to finding the GCF, even for larger numbers with multiple prime factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which represents the GCF.
Let's apply the Euclidean algorithm to 12 and 18:
- Start with the larger number (18) and the smaller number (12).
- Subtract the smaller number from the larger number: 18 - 12 = 6
- Replace the larger number with the result (6) and keep the smaller number (12).
- Since 12 > 6, repeat the subtraction: 12 - 6 = 6
- Now both numbers are 6. The process stops here.
Therefore, the GCF(12, 18) = 6
The Euclidean algorithm is particularly valuable for its efficiency in handling large numbers where the other methods become impractical.
Applications of GCF
Understanding GCFs has practical applications in various mathematical contexts:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 12/18 can be simplified by dividing both the numerator and the denominator by their GCF (6), resulting in the equivalent fraction 2/3.
-
Solving Algebraic Equations: GCFs play a role in factoring algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and solving equations more easily.
-
Geometry and Measurement: GCFs are useful in solving problems related to area, volume, and measurement conversions. For example, finding the largest square tile that can perfectly cover a rectangular floor with dimensions 12 meters and 18 meters requires finding the GCF of 12 and 18.
-
Number Theory: GCFs are a fundamental concept in number theory, a branch of mathematics dealing with the properties of integers.
GCF and Least Common Multiple (LCM)
The GCF and the least common multiple (LCM) are closely related concepts. The LCM is the smallest number that is a multiple of both numbers. For 12 and 18, the LCM is 36. There's a useful relationship between the GCF and LCM of two numbers (a and b):
GCF(a, b) x LCM(a, b) = a x b
In our example:
GCF(12, 18) x LCM(12, 18) = 12 x 18 6 x 36 = 216
This relationship can be used to find the LCM if the GCF is known, or vice versa.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. They share no common factors other than 1.
Q: Can I use a calculator to find the GCF?
A: Many scientific calculators have built-in functions to calculate the GCF (often denoted as GCD). Online calculators are also readily available.
Q: Is there a limit to the size of numbers for which I can find the GCF?
A: While the methods mentioned above are practical for a wide range of numbers, for extremely large numbers, more advanced algorithms are employed in computer science to efficiently calculate the GCF.
Conclusion
Finding the greatest common factor (GCF) is a valuable skill in mathematics. This article explored various methods for calculating the GCF, highlighting their strengths and weaknesses. From listing factors to employing the efficient Euclidean algorithm and understanding the relationship between GCF and LCM, we’ve covered a comprehensive approach to this fundamental concept. Remember that mastering GCF calculations forms a crucial foundation for success in more advanced mathematical topics. The ability to efficiently determine the GCF is not just a mathematical skill but a problem-solving tool applicable across various areas of study and practical applications. Practice makes perfect, so keep working on different examples to solidify your understanding and build confidence in your ability to tackle GCF problems with ease.
Latest Posts
Latest Posts
-
9 20 As A Percent
Sep 17, 2025
-
1 Are To Sq Ft
Sep 17, 2025
-
12 Weeks Ago From Today
Sep 17, 2025
-
400ml Is How Many Grams
Sep 17, 2025
-
Age Of Consent In Nj
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.