Lcm For 2 And 5
monicres
Sep 24, 2025 · 6 min read
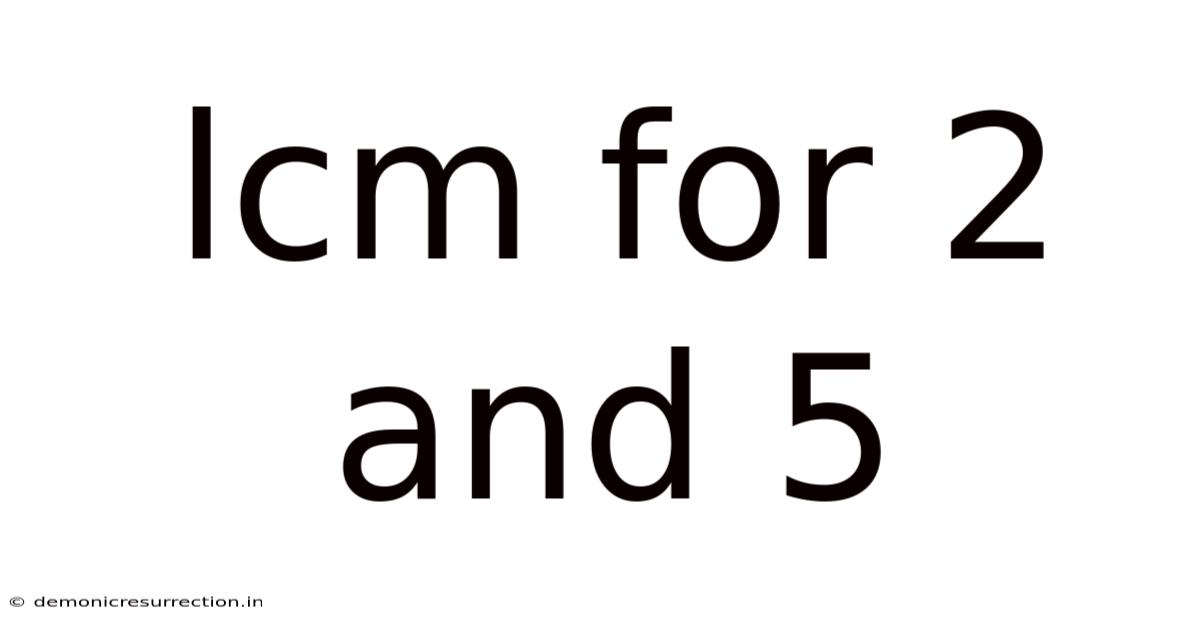
Table of Contents
Unveiling the Secrets of LCM: A Deep Dive into the Least Common Multiple of 2 and 5
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 2 and 5. However, understanding the underlying principles behind LCM calculations opens doors to more complex mathematical concepts and problem-solving skills crucial in various fields, from scheduling tasks to understanding musical rhythms. This comprehensive guide will explore the LCM of 2 and 5, detailing different methods to calculate it, explaining the underlying mathematical concepts, and exploring its practical applications. We'll also delve into related concepts and answer frequently asked questions to provide a thorough understanding of this fundamental mathematical idea.
Understanding Least Common Multiples (LCM)
Before we dive into finding the LCM of 2 and 5, let's establish a solid understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the numbers you're considering as factors.
For example, consider the numbers 3 and 4. Multiples of 3 are 3, 6, 9, 12, 15, 18... Multiples of 4 are 4, 8, 12, 16, 20... The smallest number that appears in both lists is 12. Therefore, the LCM of 3 and 4 is 12.
Calculating the LCM of 2 and 5: Three Proven Methods
Now, let's apply this understanding to find the LCM of 2 and 5. We'll explore three common methods: listing multiples, prime factorization, and using the greatest common divisor (GCD).
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
Notice that the smallest number appearing in both lists is 10. Therefore, the LCM of 2 and 5 is 10.
Method 2: Prime Factorization
Prime factorization breaks down a number into its prime factors – numbers divisible only by 1 and themselves. This method is particularly useful for larger numbers.
- Prime factorization of 2: 2 (2 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
To find the LCM using prime factorization, we take the highest power of each prime factor present in the numbers:
- The prime factors are 2 and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 5 is 5¹ = 5.
Multiplying these highest powers together: 2 x 5 = 10. Therefore, the LCM of 2 and 5 is 10.
Method 3: Using the Greatest Common Divisor (GCD)
The GCD is the largest number that divides both integers without leaving a remainder. There's a useful relationship between the LCM and GCD:
- LCM(a, b) x GCD(a, b) = a x b
Let's find the GCD of 2 and 5. Since 2 and 5 are both prime numbers and have no common factors other than 1, their GCD is 1.
Now we can use the formula:
- LCM(2, 5) x GCD(2, 5) = 2 x 5
- LCM(2, 5) x 1 = 10
- LCM(2, 5) = 10
This confirms that the LCM of 2 and 5 is indeed 10.
The Mathematical Significance of LCM
Understanding LCM extends beyond simple arithmetic. It forms the foundation of various mathematical concepts and problem-solving approaches:
-
Fractions: Finding the LCM is crucial when adding or subtracting fractions with different denominators. We find the LCM of the denominators to create equivalent fractions with a common denominator, facilitating the addition or subtraction.
-
Modular Arithmetic: LCM plays a vital role in modular arithmetic, which deals with remainders after division. This has applications in cryptography and computer science.
-
Number Theory: LCM is a key element in number theory, a branch of mathematics exploring the properties of integers. Concepts like least common multiple and greatest common divisor are fundamental building blocks in understanding the relationships between numbers.
-
Real-World Applications: LCM finds practical applications in scheduling repetitive events. For example, if bus A arrives every 2 hours and bus B arrives every 5 hours, the LCM (10 hours) determines when both buses will arrive simultaneously.
Beyond the Basics: Exploring Related Concepts
To gain a deeper understanding of LCM, exploring related mathematical concepts is beneficial. These include:
-
Greatest Common Divisor (GCD): As demonstrated earlier, the GCD is closely linked to the LCM. Understanding both concepts provides a comprehensive grasp of number relationships. Algorithms like the Euclidean algorithm efficiently calculate the GCD, which can then be used to find the LCM.
-
Prime Factorization: This method of expressing a number as a product of prime numbers is fundamental to understanding LCM and GCD calculations. It provides a structured approach to analyzing numbers and identifying their factors.
-
Modular Arithmetic: LCM finds application in solving congruences in modular arithmetic. This is particularly crucial in areas like cryptography and error-correcting codes.
-
Least Common Multiple of More Than Two Numbers: The principles of calculating the LCM extend to more than two numbers. The methods of prime factorization and using the GCD can be adapted to handle multiple numbers.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest positive integer divisible by all the given integers. The GCD (Greatest Common Divisor) is the largest positive integer that divides all the given integers without leaving a remainder. They are inversely related; a higher GCD implies a lower LCM and vice versa.
Q2: Why is the LCM of 2 and 5 important?
A2: While seemingly simple, the LCM of 2 and 5 illustrates fundamental mathematical principles applicable to more complex scenarios. It serves as a stepping stone to understanding LCM calculations for larger numbers and its applications in various fields.
Q3: Can the LCM of two numbers ever be equal to one of the numbers?
A3: Yes. If one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 2 and 4 is 4.
Q4: How can I find the LCM of larger numbers?
A4: For larger numbers, the prime factorization method is most efficient. Breaking down the numbers into their prime factors and taking the highest power of each prime factor gives you the LCM.
Conclusion: Mastering the LCM and Beyond
Understanding the LCM, particularly the LCM of seemingly simple numbers like 2 and 5, lays a strong foundation for more advanced mathematical concepts. The methods discussed – listing multiples, prime factorization, and using the GCD – provide versatile tools for calculating LCMs across various number sizes. By grasping these techniques and the underlying mathematical principles, you'll not only master LCM calculations but also enhance your overall problem-solving skills and gain a deeper appreciation for the elegance and interconnectedness of mathematics. The seemingly simple concept of the LCM of 2 and 5 opens doors to a world of mathematical exploration and practical applications, empowering you with valuable skills applicable in numerous fields.
Latest Posts
Latest Posts
-
Map Of Canada With Landforms
Sep 24, 2025
-
A Soccer Ball Is Kicked
Sep 24, 2025
-
The Book Thief Book Quotes
Sep 24, 2025
-
What Is Trickle Down Economy
Sep 24, 2025
-
Book From Dead Poets Society
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 2 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.