What Is 25 Of 16
monicres
Sep 18, 2025 · 5 min read
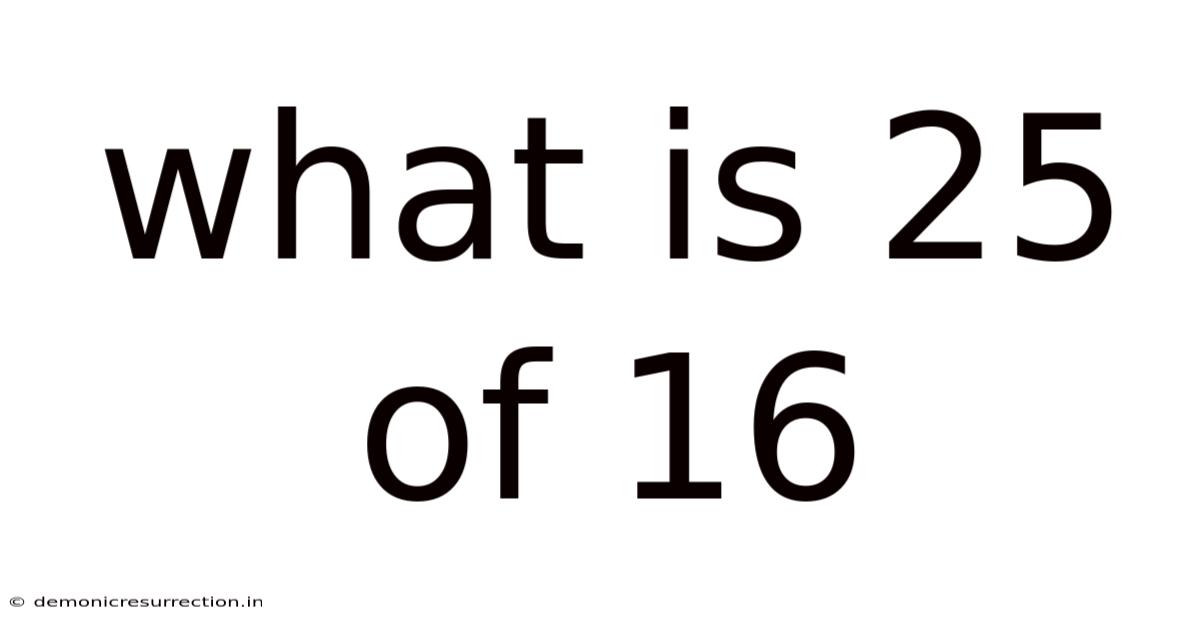
Table of Contents
What is 25% of 16? A Comprehensive Guide to Percentages
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will thoroughly explore the question "What is 25% of 16?" We'll not only solve this specific problem but also delve into the underlying concepts of percentages, providing you with the tools to confidently tackle similar calculations in the future. We'll cover multiple methods for solving percentage problems, including the formula method, the fraction method, and the decimal method. This will ensure you have a deep understanding, regardless of your current mathematical background.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol % is used to denote percentages. Essentially, a percentage represents a proportion of a whole. For example, 50% means 50 out of 100, which is equivalent to one-half (½) or 0.5. Percentages are a convenient way to express proportions because they provide a standardized scale for comparison.
Method 1: The Formula Method
The most common way to calculate a percentage of a number is using the following formula:
Percentage × Number = Result
In our case:
- Percentage = 25% = 0.25 (To convert a percentage to a decimal, divide by 100)
- Number = 16
Therefore:
0.25 × 16 = 4
So, 25% of 16 is 4.
Method 2: The Fraction Method
Percentages can also be expressed as fractions. 25% is equivalent to the fraction 25/100, which can be simplified to ¼ (one-quarter).
Using the fraction method, we can solve the problem as follows:
(¼) × 16 = 16/4 = 4
Again, we arrive at the answer: 25% of 16 is 4.
Method 3: The Decimal Method (Proportion Method)
This method involves setting up a proportion. We can express the problem as:
25/100 = x/16
Where 'x' represents the unknown value (25% of 16). To solve for 'x', we cross-multiply:
25 × 16 = 100 × x
400 = 100x
x = 400/100
x = 4
Therefore, 25% of 16 is 4. This method highlights the relationship between percentages and proportions.
Expanding on Percentage Calculations: Further Applications
The ability to calculate percentages has numerous practical applications. Let’s explore some examples:
-
Discounts: Imagine a shirt priced at $16 is on sale with a 25% discount. Using our knowledge, we know the discount is $4 (25% of $16). The final price would be $16 - $4 = $12.
-
Taxes: If a 6% sales tax is applied to a $16 item, we calculate the tax amount first: 6% of $16 = 0.06 × $16 = $0.96. The total cost including tax would be $16 + $0.96 = $16.96.
-
Tips: Calculating a tip in a restaurant is another common application. A 15% tip on a $16 meal would be 0.15 × $16 = $2.40.
-
Grade Calculations: Percentages are frequently used in education to represent grades and scores. If a student scores 20 out of 25 on a test, their percentage score would be (20/25) × 100% = 80%.
-
Financial Analysis: Understanding percentages is crucial for interpreting financial statements, analyzing investment returns, and understanding interest rates.
Solving More Complex Percentage Problems
Let’s tackle some slightly more complex scenarios to solidify your understanding:
Scenario 1: Finding the Percentage
What percentage of 20 is 5?
We can set up the equation:
x/100 = 5/20
Cross-multiplying:
20x = 500
x = 25
Therefore, 5 is 25% of 20.
Scenario 2: Finding the Original Number
15% of a number is 6. What is the number?
Let’s represent the unknown number as 'y'. We can write this as:
0.15y = 6
y = 6/0.15
y = 40
Therefore, the number is 40.
Practical Tips for Calculating Percentages
-
Mastering Decimal Conversions: The ability to quickly convert between percentages and decimals is essential for efficient calculation. Remember to divide the percentage by 100 to obtain the decimal equivalent.
-
Utilizing Calculators: While understanding the underlying principles is crucial, utilizing calculators can significantly speed up calculations, especially for more complex problems.
-
Breaking Down Complex Problems: When dealing with multifaceted percentage problems, break them down into smaller, manageable steps. This makes the problem less daunting and reduces the chance of errors.
-
Checking Your Work: Always check your answers to ensure accuracy. One method to do this is to use a different calculation method to verify your result.
Frequently Asked Questions (FAQ)
- Q: What if I need to calculate a percentage greater than 100%?
A: Percentages greater than 100% simply represent a value larger than the original number. For example, 150% of 16 is 1.5 × 16 = 24. This is commonly encountered in situations involving growth or increase.
- Q: Are there any online tools or calculators available to help with percentage calculations?
A: Yes, numerous online percentage calculators are available that can perform various percentage calculations quickly and accurately. These can serve as valuable tools for checking your work and improving your efficiency.
- Q: What is the difference between percentage increase and percentage decrease?
A: A percentage increase refers to the percentage by which a value has increased from its original value. Percentage decrease, conversely, refers to the percentage by which a value has decreased from its original value. The calculations involve finding the difference between the new value and the original value, dividing by the original value, and multiplying by 100%.
- Q: How can I improve my understanding of percentages further?
A: Practice is key. The more percentage problems you solve, the more confident and proficient you will become. Try working through various examples, utilizing different methods, and challenging yourself with more complex scenarios. You can also find numerous resources online, including tutorials and practice exercises, to further enhance your understanding.
Conclusion
Calculating percentages is a crucial skill applicable across numerous disciplines. This comprehensive guide has demonstrated multiple methods for solving percentage problems, ranging from the simple calculation of "What is 25% of 16?" to more complex scenarios involving finding percentages and original numbers. By understanding the underlying principles and practicing different techniques, you'll gain the confidence and ability to tackle any percentage problem with ease. Remember to break down complex problems, utilize resources effectively, and always check your work for accuracy. With consistent practice, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
What Is 67kg In Lbs
Sep 18, 2025
-
64 Fluid Ounces To Ml
Sep 18, 2025
-
Sword In The Stone Squirrel
Sep 18, 2025
-
Is A Seaweed A Plant
Sep 18, 2025
-
Ethnic Groups In Afghanistan Map
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.