X 2 Y 2 3
monicres
Sep 23, 2025 · 6 min read
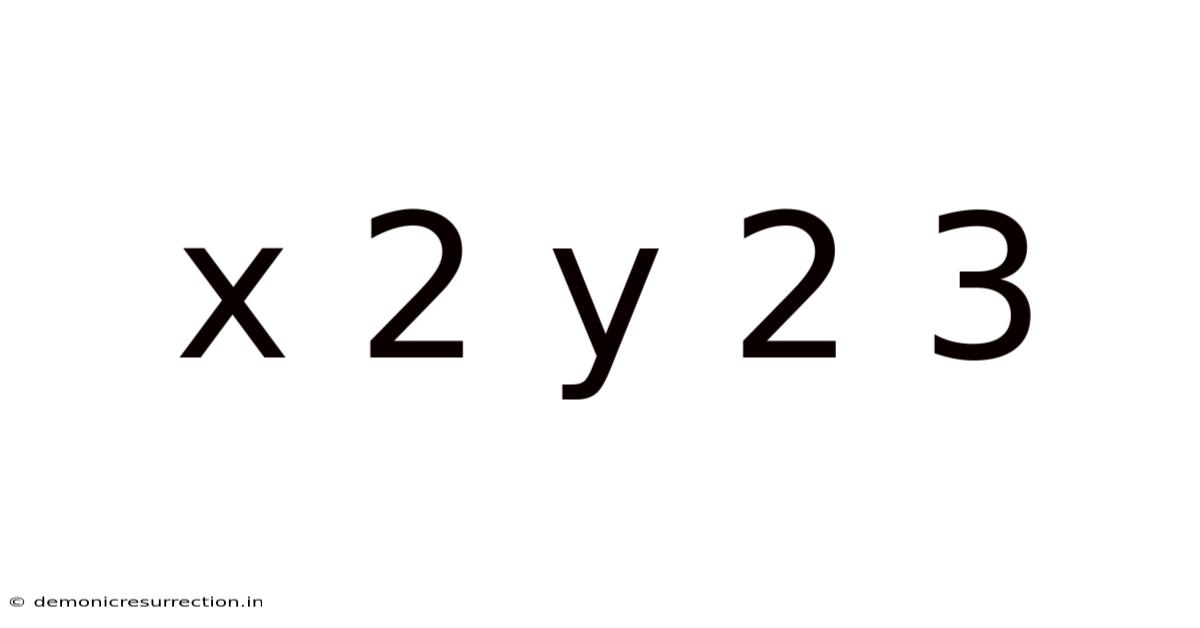
Table of Contents
Decoding the Mathematical Mystery: x² + y² = 3
The equation x² + y² = 3 might seem deceptively simple at first glance. However, this seemingly innocuous algebraic expression opens a door to a fascinating world of mathematical concepts, including coordinate geometry, number theory, and even complex numbers. This article will delve into the various aspects of this equation, exploring its solutions, graphical representation, and its implications within different mathematical contexts. We will uncover its secrets, step by step, making this complex topic accessible to everyone.
Introduction: Understanding the Equation
The equation x² + y² = 3 represents a circle in the Cartesian coordinate system. This is a fundamental concept in coordinate geometry. Remember that the general equation for a circle centered at the origin (0, 0) is x² + y² = r², where 'r' represents the radius of the circle. In our case, r² = 3, meaning the radius of the circle is √3. This immediately gives us a visual representation – a circle centered at the origin with a radius approximately equal to 1.732.
Understanding this basic geometric interpretation is crucial to understanding the solutions and implications of the equation. The solutions to the equation are all the points (x, y) that lie on the circumference of this circle.
Finding Solutions: A Numerical Approach
Finding the solutions of x² + y² = 3 involves determining the pairs of (x, y) coordinates that satisfy the equation. There are infinitely many real solutions, as any point on the circle satisfies the equation. However, we can find some specific solutions using simple algebraic manipulation and substitution.
One straightforward approach is to choose a value for x and solve for y, or vice versa. For example:
- If x = 0: Then 0² + y² = 3, which gives y² = 3, and thus y = ±√3. This provides two solutions: (0, √3) and (0, -√3).
- If y = 0: Then x² + 0² = 3, which gives x² = 3, and thus x = ±√3. This provides two more solutions: (√3, 0) and (-√3, 0).
- If x = 1: Then 1² + y² = 3, which simplifies to y² = 2, yielding y = ±√2. This gives us two more solutions: (1, √2) and (1, -√2).
This process can be repeated for numerous values of x, each yielding two corresponding y values (except for the cases where x or y is 0). The solutions are symmetrical around both the x and y axes due to the squared terms.
However, finding all solutions analytically is impossible. The infinite nature of the circle means there's an infinite number of real-valued solutions. Numerical methods are essential for approximating many solutions.
Graphical Representation: Visualizing the Circle
The equation x² + y² = 3 is best understood visually. Graphing the equation on a Cartesian plane reveals a circle centered at the origin (0,0) with a radius of √3. This visualization immediately provides a clear representation of all the possible solutions – all the points lying on the circumference of the circle.
The graph makes it clear that there are infinitely many solutions, both rational and irrational. Plotting a few of the solutions we calculated earlier helps to confirm the accuracy of our calculations and reinforces the geometrical interpretation of the equation. The visual representation is a powerful tool for comprehension and allows for a deeper understanding of the equation's nature.
Exploring Beyond Real Numbers: Complex Solutions
While the graphical representation focuses on real numbers, expanding our perspective to include complex numbers opens up another layer of complexity and richness. In the realm of complex numbers, where numbers are represented in the form a + bi (where 'i' is the imaginary unit, √-1), the equation x² + y² = 3 has an even more extensive set of solutions.
Consider a complex number z = x + yi. Then |z|² = x² + y² represents the square of the magnitude or modulus of the complex number z. Therefore, our equation x² + y² = 3 can be rewritten as |z|² = 3, or |z| = √3. This means that the equation represents all complex numbers with a magnitude (or modulus) of √3. This is no longer a simple circle in a 2D plane, but a circle in the complex plane. Every point on this circle in the complex plane represents a solution to the equation.
This extension into complex numbers significantly broadens our understanding of the equation's scope and its implications within the broader field of complex analysis.
Applications and Further Exploration
The seemingly simple equation x² + y² = 3 has implications in various areas of mathematics and beyond:
- Coordinate Geometry: The equation is a fundamental example used to understand circles, their properties, and transformations.
- Trigonometry: Solutions can be expressed using trigonometric functions, providing links between algebraic equations and trigonometric identities. Parametric equations using sine and cosine can represent all points on the circle.
- Number Theory: Investigating integer solutions or solutions within specific number fields can lead to deeper insights into number theory concepts.
- Physics and Engineering: Circles are prevalent in numerous physical phenomena, making this equation applicable to modelling various systems.
Frequently Asked Questions (FAQ)
-
Q: Are there any integer solutions to x² + y² = 3?
A: No. There are no integer solutions. The only possible integer values for x² and y² are 0 and 1, and their sums cannot equal 3.
-
Q: How can I find more solutions to the equation?
A: You can use various numerical methods, such as iterative techniques, or utilize computer programs or calculators to generate approximate solutions to a high degree of accuracy. Alternatively, parametric equations using trigonometric functions (x = √3cos(θ), y = √3sin(θ)) can generate all the solutions.
-
Q: What if the equation was x² + y² = k, where k is any constant?
A: This represents a circle centered at the origin with radius √k. If k is positive, there are real solutions. If k is negative, there are no real solutions, but there are complex solutions. If k = 0, there is only one solution (0, 0).
-
Q: What is the significance of the radius √3?
A: The radius √3 is just a specific value; the concepts discussed apply to circles of any radius. The choice of 3 is arbitrary for illustrative purposes in this article.
Conclusion: A Deeper Appreciation
The seemingly simple equation x² + y² = 3 unfolds into a surprisingly rich mathematical exploration. From its basic geometrical interpretation as a circle to its expansion into the complex plane, this equation provides a gateway to understanding fundamental concepts in various branches of mathematics. By exploring its solutions, graphical representation, and its connections to other mathematical areas, we gain a much deeper appreciation of the power and elegance of even seemingly simple algebraic expressions. This journey highlights the interconnectedness of different mathematical disciplines and the importance of visual and numerical approaches to problem-solving. Further investigation into this equation can lead to a profound understanding of mathematical principles and their practical applications.
Latest Posts
Latest Posts
-
Map Of Us With Rivers
Sep 23, 2025
-
Example Of Introduction Of Report
Sep 23, 2025
-
Bridge To Prince Edward Island
Sep 23, 2025
-
Nursing Care For Sepsis Patient
Sep 23, 2025
-
Outsourcing Is Good Or Bad
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.