X 2 Y 2 Z
monicres
Sep 15, 2025 · 7 min read
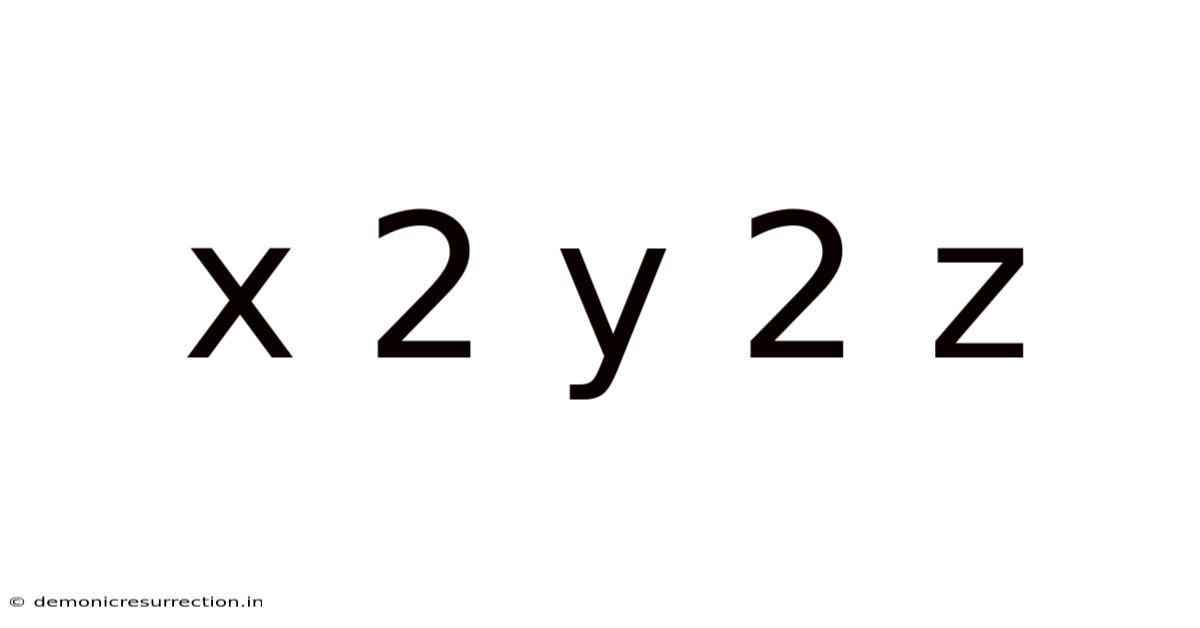
Table of Contents
Decoding x² + y² + z²: A Deep Dive into the Equation and its Applications
The equation x² + y² + z² represents a fundamental concept in mathematics with far-reaching implications across various fields. Understanding this seemingly simple equation unlocks doors to geometry, algebra, number theory, and even physics. This article will explore the equation's meaning, its geometrical interpretation, its use in solving problems, and some of its fascinating applications. We'll demystify the equation, making it accessible to a wide range of readers, from high school students to those with a more advanced mathematical background.
Introduction: Understanding the Basics
At its core, x² + y² + z² is an algebraic expression. It represents the sum of the squares of three variables: x, y, and z. These variables can represent any real numbers (positive, negative, or zero). The equation itself doesn't "solve" for anything unless it's set equal to a constant. For example, x² + y² + z² = r² has a very specific geometric meaning which we will explore later. The equation's power lies in its versatility and its ability to describe relationships between these variables within different contexts. This simplicity belies the depth of its applications.
Geometrical Interpretation: The Sphere
One of the most significant applications of x² + y² + z² is in three-dimensional geometry. When the equation is set equal to a constant, say r², we get:
x² + y² + z² = r²
This equation represents a sphere centered at the origin (0, 0, 0) with a radius of r. Each point (x, y, z) that satisfies this equation lies on the surface of the sphere. This is a powerful visualization tool that helps us understand the relationship between the variables. The value of r² dictates the size of the sphere; a larger r² means a larger sphere.
Let's break down why this equation describes a sphere. Consider a point (x, y, z) on the sphere. The distance from this point to the origin can be calculated using the distance formula in three dimensions:
Distance = √((x - 0)² + (y - 0)² + (z - 0)²) = √(x² + y² + z²)
Since this distance is the radius r, we have:
r = √(x² + y² + z²)
Squaring both sides, we arrive at the familiar equation:
x² + y² + z² = r²
This fundamental connection between the equation and the sphere is critical in various applications, especially in areas like computer graphics, physics simulations, and other fields requiring three-dimensional spatial representations.
Solving Equations and Finding Solutions
While the equation itself doesn't directly "solve" for x, y, or z, it often forms part of a system of equations. For example, consider the following system:
- x² + y² + z² = 25
- x + y = 3
- z = 4
This system can be solved by substituting the values of x + y and z into the first equation. This substitution reduces the complexity of the problem and leads us to a solution for x and y. Such systems commonly arise in various mathematical and scientific contexts, where it's crucial to find the points that simultaneously satisfy all equations in the system.
The methods used to solve such systems vary based on the nature of the equations. Substitution, elimination, and matrix methods are common techniques. Numerical methods may be required for more complex systems that lack analytical solutions. The efficiency and accuracy of these methods are crucial for obtaining correct and reliable results.
Applications in Different Fields
The seemingly simple equation x² + y² + z² has surprising breadth in its applications across various disciplines:
-
Physics: In classical mechanics, this equation is vital in describing motion in three-dimensional space. It appears in calculations involving velocity, acceleration, and forces. In electromagnetism, it helps in calculations involving electric and magnetic fields. It plays a key role in understanding the behavior of charged particles in electromagnetic fields. The concept of the sphere, directly represented by this equation, is fundamental in understanding gravitational fields and the distribution of matter in space.
-
Computer Graphics: The equation is essential for rendering 3D models and scenes. It's used to define the surfaces of spheres and other curved objects. Ray tracing and other rendering techniques rely heavily on the equation to determine the intersection of rays with these surfaces. The equation forms the basis of many algorithms used in game development, computer-aided design (CAD), and virtual reality (VR). Efficient manipulation of this equation and associated calculations are crucial for creating realistic and performant graphics.
-
Signal Processing: In signal processing, the equation often appears in calculations involving Fourier transforms and other signal analysis techniques. The concept of a sphere in a multidimensional signal space has significant applications in filter design and other aspects of signal processing.
-
Number Theory: The equation relates to important theorems and concepts in number theory. For instance, investigating integer solutions to x² + y² + z² = n (where n is an integer) leads to interesting patterns and mathematical relationships. The study of these solutions has deep connections to other areas like quadratic forms and modular arithmetic. Understanding the patterns helps to analyze and solve problems in cryptography and related fields.
-
Engineering: The equation is crucial for various engineering applications, particularly those involving three-dimensional modeling and simulations. It finds applications in structural analysis, fluid dynamics, and many other domains where understanding three-dimensional space is essential. This includes calculating stress and strain in structures, analyzing airflow around aircraft wings, and many other critical applications.
Advanced Concepts and Extensions
Beyond the basic geometrical interpretation, the equation x² + y² + z² can be extended and applied in more sophisticated ways:
-
Higher Dimensions: The concept can be generalized to higher dimensions. For example, x² + y² + z² + w² represents a hypersphere in four-dimensional space. These higher-dimensional generalizations have applications in advanced mathematical physics and other specialized fields.
-
Coordinate Systems: The equation's form changes when using different coordinate systems such as cylindrical or spherical coordinates, reflecting the flexibility of mathematical descriptions for the same geometrical object. These alternative coordinate systems offer computational advantages depending on the problem.
-
Complex Numbers: The equation can be extended to include complex numbers, leading to more intricate mathematical relationships and applications in complex analysis. This leads to a deeper understanding of the underlying mathematical structures.
-
Vector Spaces: The equation can be interpreted in the context of vector spaces, providing a richer understanding of its geometric and algebraic properties. This offers a framework for analysing more abstract structures in linear algebra and related mathematical contexts.
Frequently Asked Questions (FAQ)
-
Q: What if one or more of the variables (x, y, z) are zero?
- A: If one or more variables are zero, the equation simplifies. For example, if z = 0, the equation becomes x² + y² = r², representing a circle in the xy-plane with radius r.
-
Q: Can the equation have negative solutions?
- A: x, y, and z can be negative numbers. However, x², y², and z² will always be non-negative. The sum x² + y² + z² will therefore always be non-negative. The value of r² on the right-hand side of the equation x² + y² + z² = r² must also be non-negative.
-
Q: How is this equation used in physics?
- A: In physics, it appears in various contexts, most notably in calculations related to three-dimensional motion, distance calculations, and representing spherical objects or fields. It appears extensively in mechanics and electromagnetism.
-
Q: What are some real-world applications of this equation?
- A: Real-world applications are widespread, including 3D modeling in computer graphics, determining distances in GPS technology, and simulations in various fields of engineering.
-
Q: Are there limitations to using this equation?
- A: The equation’s limitations arise primarily when attempting to model non-spherical objects or situations requiring more complex mathematical representations beyond the scope of a simple sum of squares.
Conclusion: The Enduring Significance of x² + y² + z²
The seemingly simple equation x² + y² + z² is a powerful tool with extensive applications in diverse fields. Its geometrical interpretation as a sphere provides a visual framework for understanding its significance. From solving systems of equations to modeling complex phenomena in physics and computer graphics, this equation demonstrates the interconnectedness of seemingly disparate areas of mathematics and science. Understanding this equation provides a foundation for exploring more advanced mathematical concepts and their practical implications in the real world. Its enduring significance highlights the beauty and power of fundamental mathematical ideas. The simplicity of its form masks the depth and breadth of its applications, making it a cornerstone of mathematical understanding.
Latest Posts
Latest Posts
-
Conflict Of Interest At Work
Sep 15, 2025
-
Images Of 1 Point Perspective
Sep 15, 2025
-
Words To Describe A Relationship
Sep 15, 2025
-
A Thousand Splendid Suns Book
Sep 15, 2025
-
Books On Manners And Etiquette
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.