X Sqrt 1 X 2
monicres
Sep 19, 2025 · 6 min read
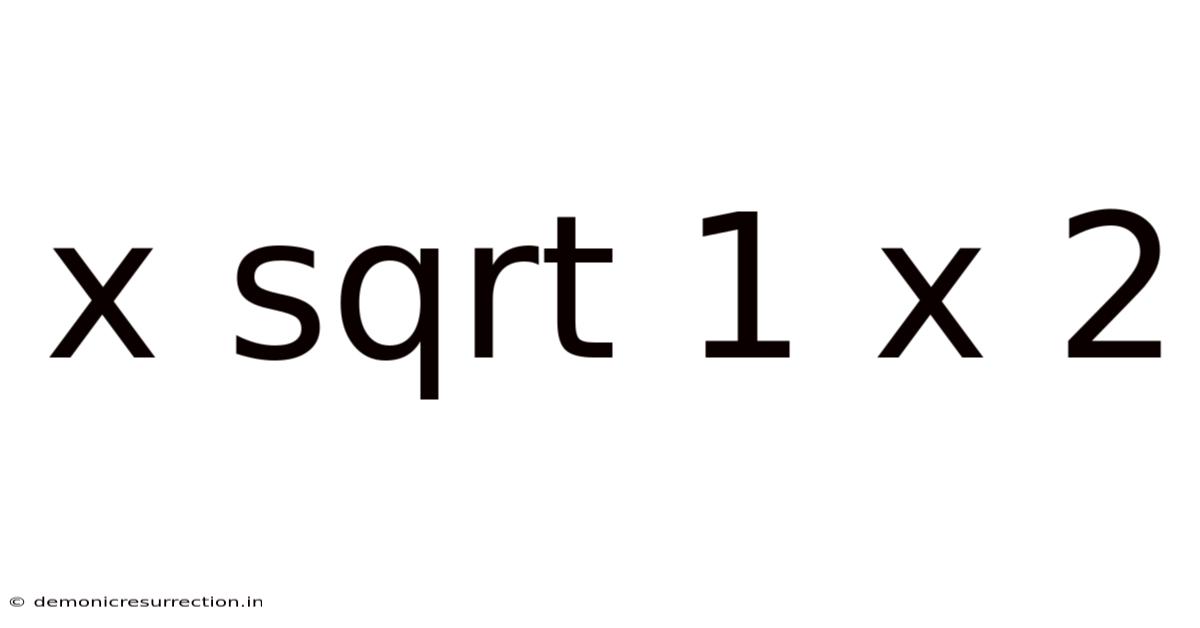
Table of Contents
Deconstructing and Exploring x√(1-x²)
This article delves into the mathematical expression x√(1-x²), exploring its properties, applications, and underlying concepts. We'll unpack its meaning, analyze its behavior, and examine its relevance within various mathematical fields. Understanding this expression requires a foundational grasp of algebra, trigonometry, and potentially, calculus. We will aim to make this accessible to a broad audience, building from basic principles to more advanced considerations.
Understanding the Expression: x√(1-x²)
At first glance, x√(1-x²) might seem daunting. However, breaking it down reveals its inherent simplicity and elegance. Let's dissect the components:
-
x: This is simply a variable, representing any real number. Its value will significantly influence the overall value of the expression.
-
√(1-x²): This is the square root of the expression (1-x²). The expression inside the square root (1-x²) is a quadratic expression. The square root operation restricts the possible outputs to non-negative values. This immediately implies a constraint on the values 'x' can take. For the expression under the square root to be non-negative, we must have 1 - x² ≥ 0, which simplifies to -1 ≤ x ≤ 1.
-
x√(1-x²): The entire expression represents the product of 'x' and the square root of (1-x²). This product will yield different values depending on the value of 'x'.
Graphical Representation and Domain
Visualizing the expression is crucial for understanding its behavior. Plotting the function y = x√(1-x²) reveals a fascinating curve.
-
Domain: The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. As mentioned earlier, the expression √(1-x²) is only defined when 1-x² ≥ 0. This leads to the domain of -1 ≤ x ≤ 1. Outside this range, the expression becomes undefined because we cannot take the square root of a negative number within the real number system.
-
Range: The range of a function is the set of all possible output values (y-values). The maximum value of the function occurs at approximately x = 0.707 (which is 1/√2), and the minimum value is at approximately x = -0.707. A detailed analysis using calculus (specifically finding critical points and evaluating the second derivative for concavity) would confirm this. The range is approximately [-0.5, 0.5].
-
Symmetry: The graph exhibits an odd symmetry. This means that f(-x) = -f(x). In simpler terms, if we reflect the graph across both the x-axis and the y-axis, we obtain the same graph. This is directly observable from the original expression: substituting -x for x results in -x√(1-(-x)²)= -x√(1-x²).
Trigonometric Interpretation and Applications
The expression x√(1-x²) has a strong connection to trigonometry. Consider a right-angled triangle with hypotenuse of length 1. Let x represent the cosine of one of the acute angles (θ). Then, by the Pythagorean theorem, the length of the opposite side will be √(1-x²), since cos²(θ) + sin²(θ) = 1. Thus, sin(θ) = √(1-cos²(θ)) = √(1-x²).
Consequently, the expression x√(1-x²) can be rewritten as cos(θ)sin(θ). This is equivalent to (1/2)sin(2θ), utilizing the double-angle formula for sine. This trigonometric representation unlocks several significant applications:
-
Physics: This expression appears in various physics contexts, such as calculating the work done by a variable force or analyzing oscillatory motion. In certain physical models, x could represent displacement or velocity, and the expression would describe aspects of the system's behavior.
-
Engineering: Similar applications arise in engineering, particularly in areas like mechanics and signal processing. The expression can be used to model specific types of oscillations or wave phenomena.
-
Geometry: Beyond the right-angled triangle example, this expression can appear in more complex geometrical problems involving circles, ellipses, or other curved shapes.
Calculus: Derivatives and Integrals
Applying calculus reveals further insights into the function's behavior:
-
Derivative: Finding the derivative (dy/dx) of x√(1-x²) involves using the product rule and chain rule of differentiation. The derivative will identify critical points (where the slope is zero), helping determine maximum and minimum values. The derivative reveals valuable information about the rate of change of the function at different points.
-
Integral: Calculating the definite integral of x√(1-x²) within the domain [-1, 1] yields the area under the curve. This requires techniques of integration, possibly involving trigonometric substitution or other advanced integration methods. The definite integral represents a key characteristic of the function's overall behavior.
Advanced Considerations and Extensions
The expression x√(1-x²) provides a springboard to more complex mathematical explorations:
-
Complex Numbers: Extending the domain to include complex numbers allows for a richer exploration of the function's behavior. The square root function becomes multi-valued in the complex plane, leading to intricate patterns and relationships.
-
Series Expansions: Approximating the function using Taylor series or other series expansions can provide valuable insights into its behavior around specific points, facilitating easier computation in certain scenarios.
-
Numerical Methods: For situations where analytical solutions are difficult to obtain, numerical methods such as Newton-Raphson or other iterative techniques can be employed to estimate values of the expression or its integral.
Frequently Asked Questions (FAQ)
-
Q: What happens when x is greater than 1 or less than -1?
*A: The expression becomes undefined in the real number system because we cannot take the square root of a negative number.
-
Q: What is the significance of the trigonometric interpretation?
*A: The trigonometric interpretation links the expression to cyclical phenomena and facilitates applications in physics and engineering involving oscillations or waves.
-
Q: How can I calculate the definite integral of the expression?
*A: This typically requires advanced integration techniques, often involving trigonometric substitution. Specific methods will depend on the desired limits of integration.
-
Q: Are there any applications beyond the ones mentioned?
*A: Yes, this expression can appear in diverse mathematical and scientific contexts. Its fundamental structure makes it relevant in various areas of modeling and analysis.
Conclusion: A Versatile Mathematical Expression
The expression x√(1-x²) might appear simple at first, but its depth and breadth are remarkable. From its straightforward algebraic form to its rich trigonometric interpretation and its applications in calculus, this expression showcases the interconnectedness of various mathematical fields. Its behavior is elegant, revealing symmetry and specific constraints on the domain and range. Understanding this expression deepens one's appreciation for the power and beauty of mathematics, illustrating how seemingly simple concepts can have far-reaching applications and implications across diverse disciplines. This exploration provides a foundation for further investigation into its properties and potential applications, encouraging a deeper dive into the fascinating world of mathematics. The versatile nature of this expression ensures its continued relevance in both theoretical and applied mathematical contexts.
Latest Posts
Latest Posts
-
Is Chlorine Acidic Or Basic
Sep 19, 2025
-
How Do Birds Have Intercourse
Sep 19, 2025
-
Flag Of The Spanish Empire
Sep 19, 2025
-
Can A Hernia Cause Diarrhea
Sep 19, 2025
-
5 12 As A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X Sqrt 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.