14 25 As A Percentage
monicres
Sep 14, 2025 · 5 min read
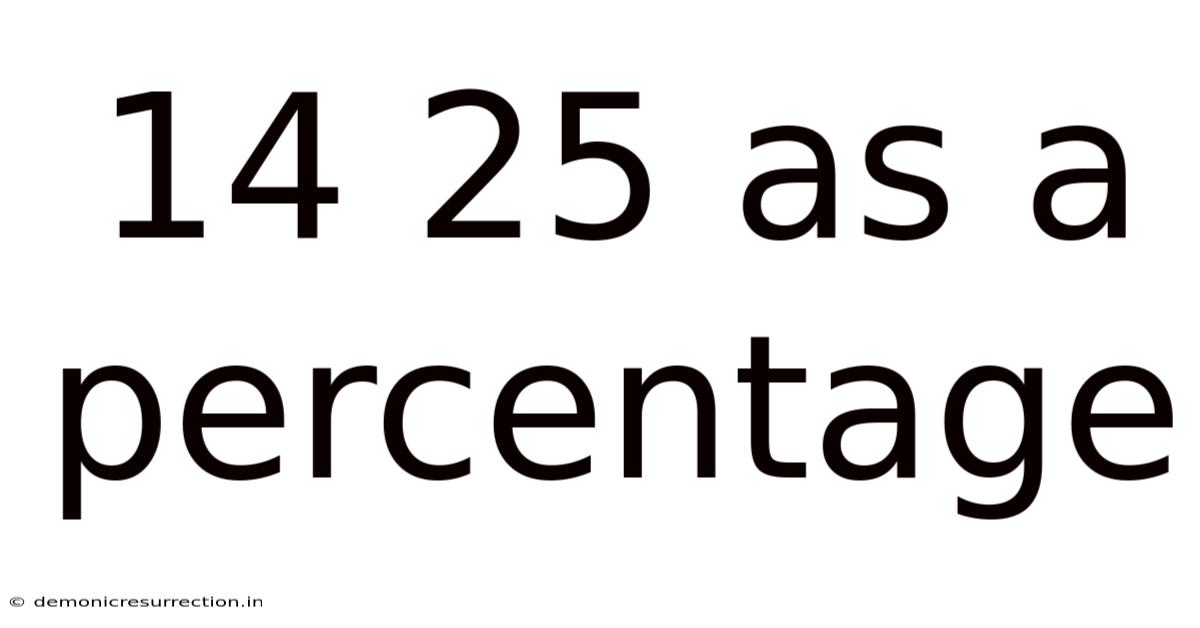
Table of Contents
Understanding 14/25 as a Percentage: A Comprehensive Guide
This article will comprehensively explain how to convert the fraction 14/25 into a percentage, providing step-by-step instructions and exploring the underlying mathematical concepts. We'll delve into various methods, addressing common questions and misconceptions along the way, making this a valuable resource for students, educators, and anyone seeking a deeper understanding of percentage calculations. Understanding percentage conversions is crucial in numerous real-world applications, from calculating grades and discounts to analyzing financial data and understanding statistics.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specific calculation of 14/25 as a percentage, let's establish a foundational understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Represent parts of a whole using a numerator (top number) and a denominator (bottom number). For example, 14/25 means 14 parts out of a total of 25 parts.
-
Decimals: Represent parts of a whole using the base-10 number system. They are expressed using a decimal point, separating the whole number from the fractional part.
-
Percentages: Represent parts of a whole as a fraction of 100. The symbol "%" signifies "per hundred" or "out of 100."
These three forms are interchangeable; you can convert one into another using specific mathematical procedures. Understanding this interconnectivity is key to mastering percentage calculations.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most straightforward method for converting 14/25 to a percentage. It involves two simple steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, simply divide the numerator (14) by the denominator (25):
14 ÷ 25 = 0.56
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.56 x 100 = 56%
Therefore, 14/25 is equal to 56%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method utilizes the principle of equivalent fractions. We aim to find a fraction equivalent to 14/25 that has a denominator of 100. Since percentages are essentially fractions out of 100, this directly gives us the percentage.
To find the equivalent fraction, we need to determine what number we must multiply the denominator (25) by to get 100. This is 4 (25 x 4 = 100). Crucially, we must multiply both the numerator and the denominator by the same number to maintain the fraction's value:
(14 x 4) / (25 x 4) = 56/100
Since 56/100 means 56 parts out of 100, this is directly equivalent to 56%.
Method 3: Using Proportions
This method employs the concept of proportions, which states that two ratios are equal if their cross-products are equal. We can set up a proportion to solve for the percentage:
14/25 = x/100
Here, 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
14 x 100 = 25 x x
1400 = 25x
Now, divide both sides by 25 to isolate 'x':
x = 1400 ÷ 25 = 56
Therefore, x = 56, meaning 14/25 is equal to 56%.
Understanding the Result: What 56% Means
The result, 56%, signifies that 14 represents 56 parts out of every 100 parts within the whole represented by 25. It's a way of expressing the proportion of 14 relative to 25 in a standardized, easily comparable format. This understanding is vital for various applications, such as:
-
Grade Calculation: If you answered 14 out of 25 questions correctly on a test, your score would be 56%.
-
Discount Calculation: A 56% discount on a product means you pay 44% (100% - 56%) of the original price.
-
Data Analysis: In statistical analysis, percentages are frequently used to represent proportions or probabilities.
-
Financial Calculations: Percentages are essential in finance for calculating interest rates, returns on investments, and profit margins.
Practical Applications and Real-World Examples
The conversion of fractions to percentages has numerous practical applications across various fields. Here are a few examples:
-
Sales and Marketing: Calculating sales growth, conversion rates, and customer acquisition costs often involves percentage calculations. For example, if a company made 14 sales out of 25 leads, their conversion rate is 56%.
-
Education: Calculating grades, analyzing student performance, and determining the pass rate of an exam all involve percentage calculations. A student scoring 14 out of 25 on a quiz achieved a 56% grade.
-
Healthcare: Tracking disease prevalence, analyzing treatment success rates, and calculating mortality rates often utilize percentages. For instance, if 14 out of 25 patients responded positively to a treatment, the success rate is 56%.
-
Environmental Science: Determining the percentage of a population affected by pollution, measuring biodiversity levels, and analyzing climate change data all rely on percentage calculations.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert fractions to percentages?
A1: Converting fractions to percentages allows for easier comparison and interpretation of proportions. Percentages provide a standardized and readily understood way to represent parts of a whole, making data analysis and communication more efficient.
Q2: Can I convert any fraction to a percentage?
A2: Yes, you can convert any fraction to a percentage using the methods outlined above. However, some fractions will result in recurring decimals or percentages.
Q3: What if the fraction has a larger numerator than denominator (an improper fraction)?
A3: You can still convert an improper fraction to a percentage using the same methods. The resulting percentage will be greater than 100%, indicating that the numerator is larger than the denominator.
Q4: Are there any online calculators to help with this conversion?
A4: While this article provides the methods, many online calculators can perform the conversion for you if you prefer. However, understanding the underlying principles is vital for true comprehension.
Conclusion: Mastering Percentage Conversions
Understanding how to convert fractions to percentages is a fundamental skill with broad applications. The three methods discussed – converting to a decimal first, finding an equivalent fraction with a denominator of 100, and using proportions – provide flexible approaches to this essential mathematical operation. By mastering these techniques, you'll be better equipped to analyze data, interpret information, and solve problems across numerous disciplines. Remember, the key is to practice and apply these methods to various scenarios to solidify your understanding and build confidence in your calculation abilities. The more you practice, the easier and more intuitive these conversions will become.
Latest Posts
Latest Posts
-
What Is A Saline Lock
Sep 14, 2025
-
List Of Er French Verbs
Sep 14, 2025
-
Is Masterbation A Mortal Sin
Sep 14, 2025
-
Things To See In Moncton
Sep 14, 2025
-
What Is 20 Of 5000
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 14 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.