Cos 2x Sin 2x Sinx
monicres
Sep 15, 2025 · 5 min read
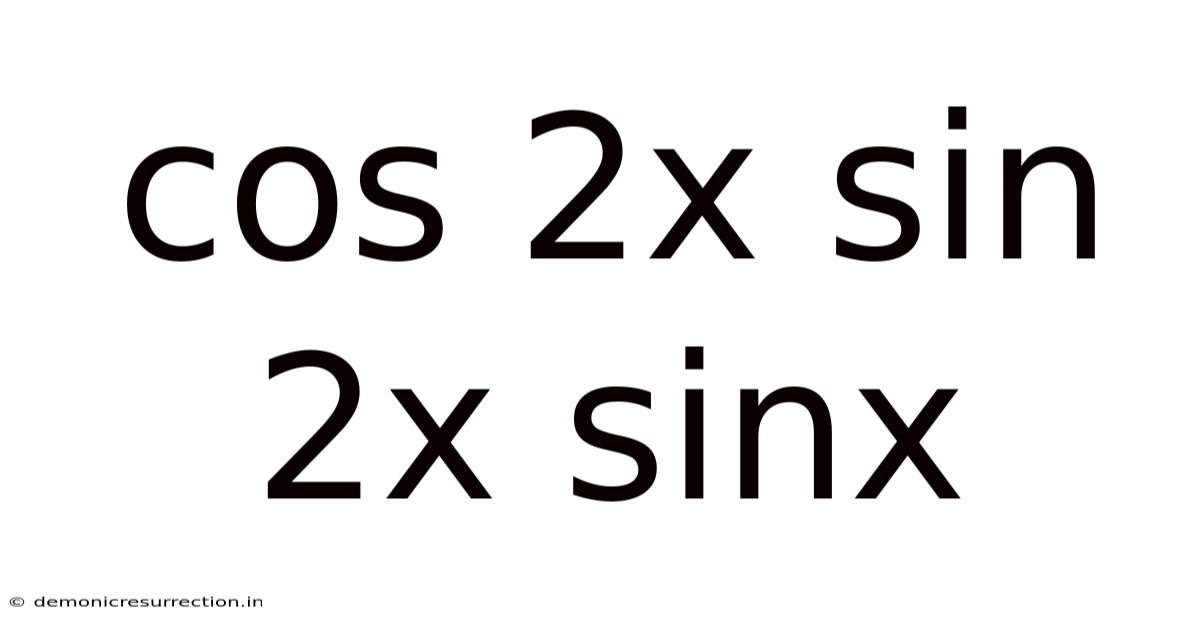
Table of Contents
Exploring the Trigonometric Expression: cos(2x)sin(2x)sinx
Understanding trigonometric identities and their manipulation is crucial for success in mathematics, particularly in calculus and physics. This article delves into the trigonometric expression cos(2x)sin(2x)sinx, exploring its simplification, potential applications, and providing a comprehensive understanding of its underlying principles. We will break down the expression step-by-step, revealing the hidden beauty and power within this seemingly complex equation. This exploration will be beneficial for students learning trigonometry, as well as those looking to refresh their knowledge of trigonometric identities and manipulation techniques.
Introduction: Deconstructing the Expression
The expression cos(2x)sin(2x)sinx presents a fascinating challenge in trigonometric simplification. At first glance, it might seem daunting, but by applying fundamental trigonometric identities and strategic manipulation, we can significantly reduce its complexity and reveal its underlying structure. This process will not only simplify the expression but also improve our understanding of trigonometric relationships and problem-solving strategies. The key lies in recognizing and utilizing double-angle and product-to-sum identities.
Step-by-Step Simplification: Unraveling the Trigonometric Puzzle
Our strategy will involve progressively simplifying the expression using well-known trigonometric identities. We will break down the process into manageable steps:
Step 1: Utilizing the Double-Angle Identity
Let's start by focusing on the sin(2x) term. We know that the double-angle identity for sine is sin(2x) = 2sin(x)cos(x). Substituting this into our original expression, we get:
cos(2x) * [2sin(x)cos(x)] * sin(x) = 2cos(2x)sin²(x)cos(x)
Step 2: Exploring Different Forms of cos(2x)
The term cos(2x) can be expressed in several ways using different double-angle identities. The most suitable choice will depend on the desired outcome. We have three primary options:
- cos(2x) = cos²(x) - sin²(x)
- cos(2x) = 2cos²(x) - 1
- cos(2x) = 1 - 2sin²(x)
Let's try using the third option, 1 - 2sin²(x), as it might lead to further simplification by combining with the sin²(x) term already present. Substituting this into our expression from Step 1:
2(1 - 2sin²(x))sin²(x)cos(x) = 2sin²(x)cos(x) - 4sin⁴(x)cos(x)
Step 3: Factoring and Further Simplification
Now, we can factor out 2sin(x)cos(x) from the expression:
2sin(x)cos(x)[1 - 2sin²(x)] = 2sin(x)cos(x)[1 - 2sin²(x)]
Notice that we've returned to a similar expression as before. This illustrates the iterative nature of trigonometric simplification – sometimes, exploring different pathways is necessary to find the most concise form. While this expression is simpler than the original, it might not be the most simplified form possible. Further manipulation might be necessary depending on the context of the problem.
Step 4: Alternative Approach using Product-to-Sum Identities
An alternative approach involves using product-to-sum identities. Recall that:
sin(A)cos(B) = ½[sin(A+B) + sin(A-B)]
Let's apply this to the expression cos(2x)sin(2x) using A=2x and B=2x:
cos(2x)sin(2x) = ½[sin(4x) + sin(0)] = ½sin(4x)
Now, let's incorporate sin(x):
½sin(4x)sin(x)
This expression utilizes the product-to-sum identity, resulting in a different but potentially equally valuable simplified form. Further simplification might be possible depending on the specific context and desired outcome.
The Power of Different Identities and Strategies
As demonstrated, multiple pathways exist to simplify the expression cos(2x)sin(2x)sinx. The choice of which identities to employ often depends on the overall context of the problem and the desired final form. Sometimes, a seemingly more complex intermediate step might lead to a simpler final result. The key is to understand the various trigonometric identities and strategically apply them to achieve the desired simplification.
Scientific Explanation and Applications
This type of trigonometric manipulation has far-reaching applications across various scientific fields. Here are a few examples:
-
Physics: In analyzing wave phenomena (like sound waves or electromagnetic waves), trigonometric functions are indispensable. Simplifying expressions like cos(2x)sin(2x)sinx can simplify complex wave equations, making them easier to solve and interpret. This is especially relevant in fields like optics and acoustics.
-
Engineering: Many engineering problems involve periodic or cyclical functions, readily described using trigonometric functions. Simplifying trigonometric expressions is crucial in areas like signal processing, electrical engineering, and mechanical engineering, enabling efficient analysis and design.
-
Computer Graphics: The rendering of realistic images in computer graphics often relies heavily on trigonometric functions to model light, shadows, and perspective. Efficient manipulation of trigonometric expressions is vital for optimizing performance and creating visually appealing graphics.
-
Mathematics: The simplification of trigonometric expressions is fundamental to advanced mathematical concepts, particularly in calculus, where trigonometric functions frequently appear in integrals and derivatives. Mastering these techniques allows for a deeper understanding of calculus and its applications.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct simplified form of cos(2x)sin(2x)sinx?
-
A: No, there isn't. Different identities and manipulation strategies can lead to different but equally valid simplified forms. The "best" form depends on the context and what is most useful for the specific problem at hand.
-
Q: What are the most important trigonometric identities to remember for simplifying expressions?
-
A: Key identities include double-angle formulas for sine and cosine, the Pythagorean identity (sin²(x) + cos²(x) = 1), and product-to-sum identities. Familiarity with these identities is essential for efficient trigonometric simplification.
-
Q: How can I practice improving my skills in simplifying trigonometric expressions?
-
A: Practice is key! Work through numerous examples, starting with simpler expressions and gradually increasing the complexity. Focus on understanding the underlying principles and strategically selecting the appropriate identities for each problem. Online resources and textbooks offer ample opportunities for practice.
Conclusion: Mastering Trigonometric Simplification
The simplification of the trigonometric expression cos(2x)sin(2x)sinx provides a valuable illustration of the power and elegance of trigonometric identities. Through careful manipulation and strategic use of identities, we can reduce complex expressions into simpler, more manageable forms. This process not only aids in problem-solving but also enhances our understanding of fundamental trigonometric relationships and their applications across various scientific and engineering disciplines. By mastering these techniques, you will unlock a deeper appreciation for the beauty and utility of trigonometry. Remember that consistent practice and a deep understanding of the underlying principles are crucial to achieving proficiency in simplifying complex trigonometric expressions.
Latest Posts
Latest Posts
-
Etats Unis Caroline Du Nord
Sep 15, 2025
-
How Is Ph Meter Calibrated
Sep 15, 2025
-
Son Of Jacob Crossword Clue
Sep 15, 2025
-
Gain For Non Inverting Amplifier
Sep 15, 2025
-
X 2 Y 2 Z
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Cos 2x Sin 2x Sinx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.